Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Удельная потенциальная энергияСодержание книги
Поиск на нашем сайте
Пусть в точке К (рис. 6) имеется частица жидкости массой С учетом полной высоты добавится еще
Разделив обе части уравнения на
Итак, удельная потенциальная энергия жидкости равна пьезометрическому напору и для всех точек на оси К рассматриваемого объема одинакова. \ Лекция 3 Приборы для измерения давления Различают абсолютное, избыточное давление, вакуум (разряжение). Если абсолютное давление больше атмосферного, наблюдают избыточное давление, если меньше – то вакуум (вакуумметрическое). Абсолютное и атмосферное давления связаны с избыточным и вакуумметрическим давлениями такими соотношениями:
Давление в жидкости измеряется либо жидкостными приборами (пьезометром, вакуумметром, дифференциальным манометром), либо механическими манометрами. Пьезометр – открытая с обоих концов стеклянная трубка, которая одним своим концом присоединяется к источнику давления (рис. 7). Для пьезометра:
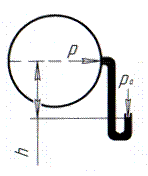
где h – высота столба жидкости в пьезометре. Следовательно, пьезометром измеряется избыточная величина пьезометрического напора жидкости. Чтобы увеличить точность отсчета, пользуются наклонными пьезометрами, микроманометрами. Вакуумметр – U-образная, открытая с обоих концов стеклянная трубка, которая одним своим концом присоединяется к источнику давления (рис. 8). Для вакуумметра
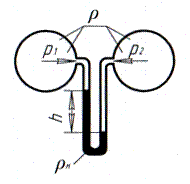
Разность давлений в жидкости измеряется дифференциальным манометром, представляющим собой U – образную, открытую с обоих концов стеклянную трубку, которая присоединяется к двум источникам давления.
Если разность давлений измеряется высотой столба данной жидкости, то показание дифференциального манометра (рис. 9).
При наличии иной жидкости в дифференциальном манометре и условии, что соединительные трубки заполнены двумя жидкостями, его показание (рис. 10)
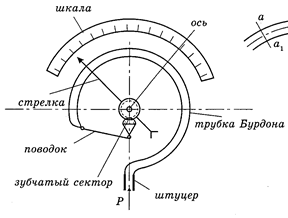
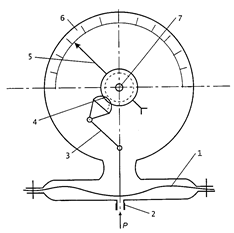
В механических манометрах давление жидкости измеряется величиной деформации гибкого элемента (полой трубки или мембраны). Жидкость через штуцер поступает в изогнутую латунную трубку – пружину эллиптического сечения и своим давлением частично ее распрямляет. Свободный конец пружины соединен с зубчатой передачей, которая при деформации приводит в движение стрелку (рис. 11). Коробка мембранного манометра (рис. 12) мембранной гофрированной тонкой металлической пластинкой или прорезиненной материей разделена на две плоскости. Под давлением поступающей в коробку жидкости мембрана деформируется и через систему рычагов поворачивает стрелку.
Силы давления жидкости на поверхности Сила давления на плоскую поверхность
Гидростатический парадокс: давление жидкости не зависит от формы сосуда, а зависит от глубины погружения площади (Г. Галилей). Сила избыточного гидростатического давления на плоскую поверхность дна сосуда площадью
На рис. 13 представлены три сосуда произвольной формы, но имеющие одинаковую площадь дна
Рис 13. Давление на плоскую горизонтальную поверхность
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 573; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.154 (0.009 с.) |

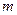 . Потенциальная энергия этой массы относительно плоскости 0-0 равна
. Потенциальная энергия этой массы относительно плоскости 0-0 равна 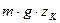 .
.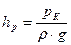 - пьезометрическая высота и полная потенциальная энергия частицы
- пьезометрическая высота и полная потенциальная энергия частицы 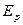 будет
будет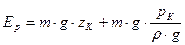 (20)
(20) , получим уравнение для удельной потенциальной энергии
, получим уравнение для удельной потенциальной энергии 
 (21)
(21)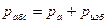 (22)
(22)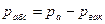 (23)
(23)
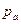
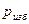
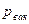
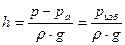 (23)
(23)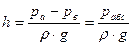 (24)
(24)

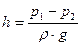 (25)
(25)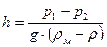 (26)
(26)

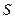 может быть определена по формуле:
может быть определена по формуле: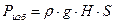 (27)
(27)