
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модель идеальной жидкости. Гидростатика, силы, действующие на жидкость. Давление в жидкости.Содержание книги
Поиск на нашем сайте
Силы, действующие на жидкость. Давление в жидкости. В следствии текучести в жидкости действуют распределенные по ее объему (массе) или поверхности силы распределенные. По этому силы, действующие на объемы жидкости являющиеся по отношению к ним внешними разделяют, на два вида: 1. Массовые (объемные) силы – в соответствии со 2-м законом Ньютона пропорциональны массе жидкости (а для однородной жидкости – по объему). К ним относятся: силы тяжести, силы инерции переносного движения, которые действуют на жидкость при отрицательном ее покое в ускоренно движущемся сосуде или при относительном движении жидкости в каналах, немешающиеся с ускорением. 2. Поверхностные силы – непрерывно распределены по поверхности жидкости и при равномерном распределении их пропорциональны площади этой поверхности. Эти силы обусловлены воздействием соседних объемов жидкости на данный объем или же воздействием других тел как твердых так и газообразных соприкасающихся с данной жидкостью (согласно 3-му закону Ньютона) Поверхностная сила ΔR действующая на площадку ΔА направлена под углом α к ней. Разложим ΔR на нормальную ΔN и тангенциальную ΔТ составляющие. ΔN – сила давления,
Массовые силы обычно относят кединицы массы, а поверхностные к единице площади. Массовые силы равны произведению массы на ускорение, поэтому единая массовая сила соответствует ускорению. Единая поверхностная сила называемая напряжением поверхностной силы раскладывается на нормальные и касательные напряжения. . Нормальная составляющая поверхностных сил называется силой давления Р, а напряжение (единичная сила) называется давлением Pср= ΔN/ ΔА Более точной величиной является давление в точке P=
Поскольку эта величина очень мала, то величину давления принято измерять в мега-паскалях Мпа1МПа = \ 106 Па. В употребляемой до сих пор технической системе единиц давление измеряется в технических атмосферах, am, 1 am = \кГ/см2 = 0,1 МПа, 1 МПа = 10 am. В технической системе единиц давление кроме технической атмосферы измеряется также в физических атмосферах, А.\А = 1,033 am. Различают давление абсолютное, избыточное и давление вакуума. Абсолютным давлением называется давление в точке измерения, отсчитанное от нуля. Если за уровень отсчёта принята величина атмосферного давления, то разница между абсолютным давлением и атмосферным называется избыточным давлением.
Pізб=Pаб-PaЕсли давление, измеряемое в точке ниже величины атмосферного давления, то разница между замеренным давлением и атмосферным называется давлением вакуума Pвак=Ра-РабсИзбыточное давление в жидкостях измеряется манометрами. Это весьма обширный набор измерительных приборов различной конструкции и различного исполнения 5. Свойства гидростатического давления. Дифференциальные уравнения равновесия жидкости (Уравнение Эйлера, вывод). В покоящейся жидкости силы вязкости не проявляются, по этому на неподвижную жидкость из поверхностных сил действуют только силы давления, таким образом в неподвижной жидкости возможен лишь один вид напряжения – напряжение сжатия, т.е. гидростатическое давление. Это давление имеет свойства: Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости. Свойство 2. Гидростатическое давление неизменно во всех направлениях. Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.При движении реальной рабочей жидкости возникают касательные напряжения, соответственно давление в реальной рабочей жидкости указанными свойствами не обладает.
Это уравнение относится к идеальной жидкости. dx, dy, dz – размеры объема по координатным осям. А – середина. Дано жидкое тело, массой М, плотностью
F= f(Fx;Fy; Fz)
Обе части полученной системы можно разделить на константу
6. Интегрирование уравнений Эйлера. Поверхности равного давления. Основное уравнение гидростатики (вывод). 1. Поверхность равного давления – пов-ть проходящая через точки с одинаковым давлением (ПРД) P=const =>dp=0; ρ≠0 Xdx+Ydy+Zdz = 0 –ур-е ПРд в диф. L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAq16XSb4A AADbAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdC/5DuAPuNB0V0Y5RRFDUjU9we22ubZnm pjSx1r83C8Hl4byn88YUoqbK5ZYV/PYiEMSJ1TmnCi7nVXcMwnlkjYVlUvAiB/NZuzXFWNsnH6k+ +VSEEHYxKsi8L2MpXZKRQdezJXHg7rYy6AOsUqkrfIZwU8h+FI2kwZxDQ4YlLTNK/k8Po+Cwpck+ X8j7a3C+It3Wu7qORkp1fprFHwhPjf+KP+6NVjAMY8OX8APk7A0AAP//AwBQSwECLQAUAAYACAAA ACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQIt ABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVsc1BLAQIt ABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4bWwueG1s UEsBAi0AFAAGAAgAAAAhAKtel0m+AAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9kb3ducmV2 LnhtbFBLBQYAAAAABAAEAPUAAACDAwAAAAA= " fillcolor="#4f81bd" strokecolor="#385d8a" strokeweight="2pt"/>
Основное ур-е гидростатики. Оно позволяет уст-ть закон распределения давления в покоящейся жидкости. Для этого рассмотрим. Объем покоящ. ж. в декарт. сист. корд., при усл. дейст-я одной массовой силы – силы тяжести
dp=ρ(Xdx+Ydy+Zdz) x=0 y=0 z=gdp=ρgdzp=ρgz+c P=P0+ ρgh - давление любой т. в ж. Р0 - давл. на пов-ти. ρgh-весовое(избыточно) давление, обусловленное весом столба жид-ти. Р0=Ратм – абсол. гидрастатическое давление Рабс=Ратм+ρgh
7. Уравнение гидростатического напора (вывод). Приборы для измерения давления.
dP=ρ(Xdx+Ydy+ Zdz) x=0; y=0; z=-g; dp= -ρgh=>dz+dp/ρg=o z+P/ρg=const = Hг.с. –гидростат. напор Zа+Pа/ρg = Zв+ Pв/ρg = const z-геом. высота P/ρg- пьезометрическая высота [P/ρg] = (FL^3T^2)/(L^2ML) = L
1. Рабс>Ратм Ризб,А = Рабс,А–Ратм Ризб,А = ρgh =>h= Ризб,А/ρg, P0 = 0,1 MПа hв = 10^5/(10^3∙9,81) = 10,19 м Рабс,А = Ратм + ρgh 2. Рабс<Ратм. Рабс + ρghвак = Ратм =>Ратм – Рабс = ρghвак.
Рвак= Ратм - Рабс
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 357; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.45.22 (0.007 с.) |

 ΔТ – сила трения.
ΔТ – сила трения.
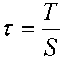 Напряжение тангенциальной составляющей поверхностной силы Т (касательное напряжение
Напряжение тангенциальной составляющей поверхностной силы Т (касательное напряжение  ) определяется аналогичным образом (в покоящейся жидкости Т=0).
) определяется аналогичным образом (в покоящейся жидкости Т=0). Величина давления (иногда в литературе называется гидростатическим давлением) в системе СИ измеряется в паскалях.
Величина давления (иногда в литературе называется гидростатическим давлением) в системе СИ измеряется в паскалях. Дифференциальное уравнение равновесия жидкости.
Дифференциальное уравнение равновесия жидкости. , которое находится в равновесии под действием внешних сил. Равнодействующую этих сил обозначим F.
, которое находится в равновесии под действием внешних сил. Равнодействующую этих сил обозначим F. Выберем декартову систему координат в которой находится тело. Сила F может быть разложена на 3 составляющие:
Выберем декартову систему координат в которой находится тело. Сила F может быть разложена на 3 составляющие: Где
Где  - это в соответствии со 2-м законом Ньютона – проекции ускорений, вызываемых внешними силами на соответствующие координатные оси. Выделим в жидком теле бесконечно малый объем с центром в точке А в форме прямоугольного параллелепипеда, грани которого параллельны координатным осям. Мысленно отбрасываем окружающую параллелепипед жидкую среду. Заменяем жидкую среду эквивалентными силами. Поскольку жидкое тело находится в равновесии, соответственно и выделенный объем, то
- это в соответствии со 2-м законом Ньютона – проекции ускорений, вызываемых внешними силами на соответствующие координатные оси. Выделим в жидком теле бесконечно малый объем с центром в точке А в форме прямоугольного параллелепипеда, грани которого параллельны координатным осям. Мысленно отбрасываем окружающую параллелепипед жидкую среду. Заменяем жидкую среду эквивалентными силами. Поскольку жидкое тело находится в равновесии, соответственно и выделенный объем, то - условие равновесия вдоль оси х.
- условие равновесия вдоль оси х.  - проекция на ось х элементарной массовой силы.
- проекция на ось х элементарной массовой силы.  Элементарная масса прямоугольного параллелепипеда:
Элементарная масса прямоугольного параллелепипеда: 
 - элементарный объём нашего параллелепипеда
- элементарный объём нашего параллелепипеда
 и
и  - давление в точках 1 и 2. А – центр тяжести рассматриваемого элементарного объёма. Давление в точке А=р. Направление оси х может быть представлено частной производной:
- давление в точках 1 и 2. А – центр тяжести рассматриваемого элементарного объёма. Давление в точке А=р. Направление оси х может быть представлено частной производной: 



 и получим:
и получим: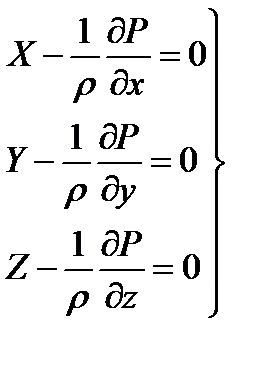 Сложим все 3 уравнения и получим следующую формулу:
Сложим все 3 уравнения и получим следующую формулу:
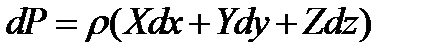
 - основное уравнение гидростатики.
- основное уравнение гидростатики. c=p0-ρgzP=P0+ ρg(z-z0)
c=p0-ρgzP=P0+ ρg(z-z0) Ур-егидростатич. напора позволяет уст-ть связь между давлением и геометрической высотой расположения точки, относительно выбранной горизонтальной плоскости сравнения
Ур-егидростатич. напора позволяет уст-ть связь между давлением и геометрической высотой расположения точки, относительно выбранной горизонтальной плоскости сравнения Приборы для измерения давления: жидкостные, механические, электрические.
Приборы для измерения давления: жидкостные, механические, электрические.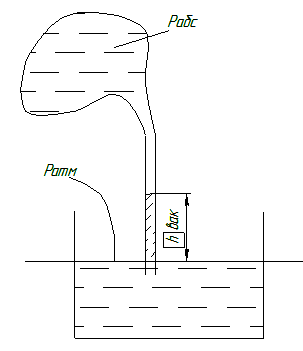 Рвак = ρghвак.
Рвак = ρghвак.


