Разветвленный и сложный трубопроводы. Основные расчетные зависимости.
Похожие статьи вашей тематики
Разветвленное соединение. Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение - место разветвления (или смыкания) труб.
 Рис. 6.5. Разветвленный трубопровод Рис. 6.5. Разветвленный трубопровод
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три трубы 1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 6.5, а). Геометрические высоты z1, z2 и z3 конечных сечений и давления P1, P2 и P3 в них будут также различны. Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме расходов в каждом трубопроводе: Q = Q1 + Q2 + Q3. Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода, получим (пренебрегая разностью скоростных высот) 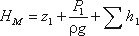 . Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как это делалось в п.6.1), получаем HM = Hст 1 + KQ1m. Аналогично для двух других трубопроводов можно записать HM = Hст 2 + KQ2mHM = Hст 3 + KQ3m. Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM. Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) - сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3, а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM> Hст1. . Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как это делалось в п.6.1), получаем HM = Hст 1 + KQ1m. Аналогично для двух других трубопроводов можно записать HM = Hст 2 + KQ2mHM = Hст 3 + KQ3m. Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM. Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) - сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3, а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM> Hст1.
 Сложные трубопроводы Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б). Сложные трубопроводы Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).
Рис. 6.6. Схемы сложных трубопроводов
  Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б).магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE. Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M - N и избыточные давления в конечных точках PB и PD и PE. Для этого случая возможны два вида задач: Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М. Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви. Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно: уравнение расходов: Q = QB + QD + QE - уравнение равенства потребных напоров для ветвей CD и CEHст D + KCDQDт = Hст E + KCEQEт - уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕDHст B + KABQBт = Hст D + KCDQDт + KAC(QD + QE)т выражение для потребного напора в точке М Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом: 1) сложный трубопровод разбивают на ряд простых; Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б).магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE. Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M - N и избыточные давления в конечных точках PB и PD и PE. Для этого случая возможны два вида задач: Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М. Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви. Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно: уравнение расходов: Q = QB + QD + QE - уравнение равенства потребных напоров для ветвей CD и CEHст D + KCDQDт = Hст E + KCEQEт - уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕDHст B + KABQBт = Hст D + KCDQDт + KAC(QD + QE)т выражение для потребного напора в точке М Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом: 1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п.6.2). Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения жидкости.
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA3f3O5MUA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbESPQYvCMBSE78L+h/AEb5paUKRrFCmIsuhBt5e9vW2e bbF56TZZrf56Iwgeh5n5hpkvO1OLC7WusqxgPIpAEOdWV1woyL7XwxkI55E11pZJwY0cLBcfvTkm 2l75QJejL0SAsEtQQel9k0jp8pIMupFtiIN3sq1BH2RbSN3iNcBNLeMomkqDFYeFEhtKS8rPx3+j 4Ctd7/HwG5vZvU43u9Oq+ct+JkoN+t3qE4Snzr/Dr/ZWK4ijMTzPhCMgFw8AAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQDd/c7kxQAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA " filled="f" stroked="f" strokeweight=".5pt"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEATMdnecIA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdD/gP4QqzG1MLM0g1LVIQRcaFj427a3Nt i81NbaJ2/PrJQnB5OO9Z1ptG3KlztWUF41EEgriwuuZSwWG/+JqAcB5ZY2OZFPyRgywdfMww0fbB W7rvfClCCLsEFVTet4mUrqjIoBvZljhwZ9sZ9AF2pdQdPkK4aWQcRT/SYM2hocKW8oqKy+5mFKzz xQa3p9hMnk2+/D3P2+vh+K3U57CfT0F46v1b/HKvtII4CmvDmXAEZPoPAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQBMx2d5wgAAANwAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA " filled="f" stroked="f" strokeweight=".5pt"> L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEADncH8MMA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERPS4vCMBC+L/gfwgje1lRhXa1GkYKsiHvwcfE2NmNb bCa1iVr99ZsFwdt8fM+ZzBpTihvVrrCsoNeNQBCnVhecKdjvFp9DEM4jaywtk4IHOZhNWx8TjLW9 84ZuW5+JEMIuRgW591UspUtzMui6tiIO3MnWBn2AdSZ1jfcQbkrZj6KBNFhwaMixoiSn9Ly9GgWr ZPGLm2PfDJ9l8rM+zavL/vClVKfdzMcgPDX+LX65lzrMH33D/zPhAjn9AwAA//8DAFBLAQItABQA BgAIAAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1s UEsBAi0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxz UEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXht bC54bWxQSwECLQAUAAYACAAAACEADncH8MMAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rv d25yZXYueG1sUEsFBgAAAAAEAAQA9QAAAIgDAAAAAA== " filled="f" stroked="f" strokeweight=".5pt"> 38.Гидравлический удар. Формула Жуковского для прямого и не прямого удара (вывод).Скорость распространения ударной волны при гидравлическом ударе.
Гидро удар – колебательный процесс, возникающий в упругом трубопроводе с капельной жидкостью, при внезапном изменении скорости её движения. Этот процесс характеризуется чередованием резких повышений и понижений давления.Изменение давления в жидкости при этом тесно связано с её упругими деформациями и упругими деформациями стенок трубопровода. В результате силового взаимодействия между движущимися и остановленными частицами жидкости возникает переходная область наз. Ударной волной, которая со скоростью С перемещается по трубопроводу. Tср – время фазы гидравлического удара.Tср=2 l /C
Форм. Жуковского для прямого и непрямого удара:
Тзак<Tср– удар прямой Тзак>Tср – удар непрямойТзак – время закрытия проходного сеч.
Для основного объёма применим теорему об изменении кол-ва движений
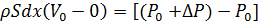 Sdt Sdt
 V0dx = V0dx = 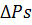 dt => dt =>  = =  ; ;  = = 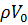 С – формула Жуковского для прямого удара С – формула Жуковского для прямого удара
 = = 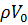 С С 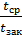 – формула Жуковского для непрямого гидроудара – формула Жуковского для непрямого гидроудара
С=  Еж – модуль упругости ж-сти, МПа Еж – модуль упругости ж-сти, МПа
Етр – модуль упругости материала стенки трубопровода
D – диаметр трубопровода
δ – толщина стенки трубопровода
|



 Рис. 6.5. Разветвленный трубопровод
Рис. 6.5. Разветвленный трубопровод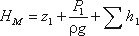 . Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как это делалось в п.6.1), получаем HM = Hст 1 + KQ1m. Аналогично для двух других трубопроводов можно записать HM = Hст 2 + KQ2mHM = Hст 3 + KQ3m. Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM. Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) - сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3, а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM> Hст1.
. Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как это делалось в п.6.1), получаем HM = Hст 1 + KQ1m. Аналогично для двух других трубопроводов можно записать HM = Hст 2 + KQ2mHM = Hст 3 + KQ3m. Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1, Q2 и Q3 и HM. Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) - сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для ветвей отмечены цифрами 1, 2 и 3, а суммарная кривая потребного напора для всего разветвления обозначена буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство HM> Hст1. Сложные трубопроводы Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).
Сложные трубопроводы Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).
 Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б).магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE. Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M - N и избыточные давления в конечных точках PB и PD и PE. Для этого случая возможны два вида задач: Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М. Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви. Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно: уравнение расходов: Q = QB + QD + QE - уравнение равенства потребных напоров для ветвей CD и CEHст D + KCDQDт = Hст E + KCEQEт - уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕDHст B + KABQBт = Hст D + KCDQDт + KAC(QD + QE)т выражение для потребного напора в точке М Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом: 1) сложный трубопровод разбивают на ряд простых;
Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б).магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q B и QD и QE. Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости M - N и избыточные давления в конечных точках PB и PD и PE. Для этого случая возможны два вида задач: Задача 1. Дан расход Q в основной магистрали MA. Необходимо определить расходы QB и QD и QE, а также потребный напор в точке М. Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в каждой ветви. Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа конечных ветвей, а именно: уравнение расходов: Q = QB + QD + QE - уравнение равенства потребных напоров для ветвей CD и CEHст D + KCDQDт = Hст E + KCEQEт - уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕDHст B + KABQBт = Hст D + KCDQDт + KAC(QD + QE)т выражение для потребного напора в точке М Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует строить следующим образом: 1) сложный трубопровод разбивают на ряд простых;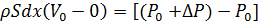 Sdt
Sdt V0dx =
V0dx = 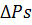 dt =>
dt =>  =
=  ;
; 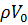 С – формула Жуковского для прямого удара
С – формула Жуковского для прямого удара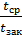 – формула Жуковского для непрямого гидроудара
– формула Жуковского для непрямого гидроудара Еж – модуль упругости ж-сти, МПа
Еж – модуль упругости ж-сти, МПа


