
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристика и виды сложных сужденийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мы рассмотрели простые категорические суждения. Но мышление в равной мере использует и сложные суждения. В чем особенность сложного суждения? В использовании логических связок и их логической характеристике. Сложным называется суждение, состоящее из нескольких простых суждений, соединенных с помощью логических связок «Λ»; «&» (конъюнкции) – соответствует союзу «И»; «V» (слабая дизъюнкция) – соответствует союзу «или-или»; «V» (сильная дизъюнкция) – соответствует союзу «либо-либо»; «→» (импликация) – соответствует союзу «если…, то…»; «↔» (эквиваленсия) – соответствует союзу «если и только если, … то…»; «─», «┐» - отрицание. В сложных суждениях важное значение имеют связки, т.к. они определяют структуру и логические характеристики суждений. Несмотря на то, что грамматические союзы и логические связки сложных суждений тождественны по форме, они различаются по функциям и значениям. Используя союзы в грамматике, при составлении сложных предложений, мы следим за тем, чтобы предложение имело смысловое содержание и было построено по правилам грамматики того или иного языка. В логике же, используя союзы (логические связки) для образования сложных суждений, мы рассматриваем их с точки зрения истинности или ложности. Эти два свойства суждения – быть истинным или ложным – называются логическими значениями «истина» или «ложь». Напоминаю, что для обозначения суждений используют пропозициональные переменные: А, В, С или а, в, с; «(» - левую скобку; «)» - правую скобку. Иных знаков нет.
Из перечисленных знаков можно образовать формулы, т.е. знаковые эквиваленты простых и сложных суждений согласно следующему определению: 1) Пропозициональная переменная А, В, С, …. Есть формула; 2) Если А – произвольная формула, то (АΛВ), (АVВ), (А V), (А→В), (А↔В) также формулы. Других формул нет. Некоторые части формулы сами могут быть формулами, тогда мы говорим о подформулах. Например, (А Λ В) → (А VВ) - читается: «если А и В, то А или В». Если в формуле несколько логических связок, то главной будет та, которая при построении вводится последней. Так, в формуле (А→(АVВ) главной связкой будет связка (союз) «→» («если, …то…»). Теперь рассмотрим значение (смысл) логических связок. Отрицание. Отрицанием формулы А называется формула «не - А», (
Таблица 1.
Видим, что отрицающие друг друга формулы не могут быть вместе истинными и ложными. Если одна истинна, то другая ложна и наоборот. Отрицающими являются следующие пары суждений: Первая пара: «Все S есть Р» и «Некоторые S не есть Р»; Вторая пара: «Ни одно S не есть Р» и «Некоторые S есть Р»; Третья пара: «Это S есть Р» и «Это S не есть Р».
Различают два вида отрицания: внутреннее отрицание и внешнее отрицание. Внутреннее отрицание указывает на несоответствие предиката (Р) субъекту (S) суждения. Например, «Некоторые студенты не посещают занятия». Внешнее отрицание – это отрицание всего суждения. Например, «Неверно, что Донецк находится на севере Украины». Теперь рассмотрим сложные суждения, образованные с помощью логических связок (союзов). Конъюнкция (от лат. conjunction – союз, связь) – это соединительные суждения, образованные с помощью союза «Λ», «&», т.е. «и». Конъюнктивным называется сложное суждение, образованное из простых суждений при помощи связки «Λ». Пример: «Студенты заняли места в аудитории и лекция началась». Формула: «АΛВ». При помощи конъюнктивной связки можно соединить два и более простых суждений. Пример: «После звонка студенты заняли места в аудитории, вставанием приветствовали преподавателя и лекция началась». Формула: «АΛВΛС». Определение конъюнкции. Конъюнкция – это логическая операция, при которой два и более суждений объединяются в сложное суждение, которое является истинным только тогда, когда каждое из исходных суждений истинно, и является ложным, когда, по крайней мере, одно из исходных суждений ложно. Значение истинности сложного конъюнктивного суждения зависит от истинностных значений входящих в него простых суждений и выражается в виде таблицы истинности:
Таблица 2
Из таблицы видно, что конъюнктивное высказывание истинно только в одном случае: когда все входящие в него простые высказывания истинны и ложно, если одно из входящих в него суждений ложно. Например, «Киев стоит на Днепре и является столицей Украины» - истинно. Но высказывание «Киев стоит на Днепре и является столицей Белоруссии» будет ложно. В учебниках по логике отмечается, что значение конъюнктивного суждения не зависит от порядка его членов, т.е. для конъюнкций справедлив закон коммутативности (переместительности): АΛВ эквивалентно ВΛА. Но этот закон действует не всегда. Исключением является, например, суждение: «Подул сильный ветер и деревья закачались». Если в этом суждении члены конъюнкции поменять местами, то суждение будет бессмысленным, ибо получим: «Деревья закачались, и подул сильный ветер».
Разделительное (дизъюнктивное – от лат. Disjunction – разобщение, различение) суждение.
Дизъюнктивным называется сложное суждение, образованное из двух или большего числа простых суждений посредством логических связок «или», «либо». Например, «После занятий мы поедем домой или пойдем в кино». «Договор купли-продажи может быть заключен в устной или письменной форме». Общая формула дизъюнктивного суждения имеет вид: «(АVBVC)» - читается: «А или В или С…». Существует два вида дизъюнкции: соединительно-разделительная (слабая) и исключающе-разделительная (сильная дизъюнкция). Рассмотрим их: 1) Союз «или» («V») характеризует соединительно-разделительную или слабую дизъюнкцию и употребляется, например, в следующем суждении: «Студент Шевченко, успешно сдавший экзамены, очень способный или очень прилежный». Здесь утверждается следующее: 1) студент Шевченко успешно сдал экзамены или потому, что он способный, или потому, что он прилежный; или потому, что он и способный и прилежный одновременно; 2) студент Шевченко не мог сдать успешно экзамены, если бы он не был ни способным, ни прилежным. Мы видим, что данное суждение будет истинным, когда, по крайней мере, одно из исходных простых суждений будет истинным. И, что сложное суждение будет ложным, когда оба исходных суждения будут ложными. Поэтому, слабая дизъюнкция, когда союз «или» употребляется в соединительно-разделительном смысле, определяется следующим образом: «соединительно-разделительная дизъюнкция – союз «или» есть такая связь двух или более исходных суждений, образующих новое сложное суждение, которое будет истинным лишь тогда, когда, по крайней мере, одно из исходных суждений истинно; в том же случае, когда каждое из них ложно, новое суждение будет ложным» см. табл.3.
Таблица 3
Из таблицы видно, что сложное суждение «АVВ» будет истинным в первых трех случаях: 1) когда и А и В истинные; 2) когда А истинно, а В ложно; 3) когда А ложно, а В истинно и сложное суждение ложно, когда и А и В ложны.
Условия, при которых строгая дизъюнкция является истинной, записывается в таблице 4:
Таблица 4
Из таблицы видно, что сложное суждение будет истинным только в двух случаях: 1) когда А истинно, а В ложно; 2) когда А ложно, а В истинно, в остальных случаях оно ложно. Примеры таких суждений: «Деревья бывают либо широко-лиственные, либо хвойные». «Во время летних каникул я поеду в Киев, либо в Одессу». В этих случаях союз «или» разделяет простые суждения так, что они одновременно не могут быть истинными, т.к. деревья не могут быть одновременно широко-лиственными и хвойными. Если они хвойные, то не широко-лиственные. На летние каникулы я буду либо в Киеве, либо в Одессе. Но одновременно быть в Киеве и в Одессе невозможно, поскольку они находятся в разных местах. Как видим, при строгой дизъюнкции: либо А либо В – каждый член дизъюнкции является альтернативой для других членов. При истинности А будет ложным В, при истинности В будет ложным А.
О дизъюнктивных суждениях нужно помнить еще следующее: 1) При использовании дизъюнктивных суждений в обычной речи возникают некоторые особенности. Чтобы подчеркнуть строго-разделительный характер суждения, вместо союза «или» используют союз «либо». Например, говоря, что «Человек болен или расстроен», мы можем допустить, что Человек может быть и больным и расстроенным одновременно. Но если же скажем: «Человек либо болен, либо расстроен», то предполагаем одно из двух. Как видим, замена союза «или» на союз «либо» придает ему исключающее значение и меняет логический смысл суждения. 2) Вторая особенность дизъюнктивных суждений связана с логическим анализом юридических текстов (законов, договоров, судебных речей и т.п.). Здесь могут возникнуть два обстоятельства. Первое обстоятельство связано с языковой формой выражения дизъюнктивных суждений. Так как в грамматике нет однозначных союзов для отличия слабой дизъюнкции от сильной, то вопрос о логической характеристике суждения решается в результате анализа содержания самого явления и высказывания о нем. Например, ст.552 ГК РФ, предусматривающая условия перехода наследства к государству записана так: «Наследственное имущество по праву наследования переходит к государству: если имущество завещано государству; если у наследователя нет наследников…; если все наследники лишены завещателем права наследования; если ни один из наследников не принял наследства…» (АVBVCVД). Здесь союзы «или», «либо» отсутствуют. Но из анализа высказывания можем отметить, что это слабая дизъюнкция, т.к. каждое из указанных условий не исключает их одновременное действие. Второе обстоятельство таково: там, где применяются правовые нормы, логические дизъюнкции имеют особое значение. Исходя из условий истинности дизъюнктивных суждений, мы делаем заключение, что для признания истинности суждения в целом, достаточно истинности одного члена. Но в то же время необходимым условием истинности дизъюнктивного суждения является то, когда все его члены взяты вместе. В этом случае различают два вида дизъюнктивных суждений: - полные (или закрытые); - неполные или открытые.
В полной дизъюнкции перечислены все признаки или все виды определенного рода. Например, «Настоящий договор купли-продажи расторгается: если одна из сторон своевременно не поставит товар, а другая своевременно не перечислит деньги или предпримет действия, наносящие ущерб другой стороне, или в своей деятельности нарушит юридические нормы предпринимательства». В этом суждении перечислены все признаки, ведущие к расторжению договора. Она полная. Символическая запись: <AVBVC>.
В неполных дизъюнкциях даны не все признаки или виды определенного рода. Символически их можно представить: AVBV…. В грамматических предложениях неполная дизъюнкция выражается словами: «и так далее», «и другие», «и т.п.», «иные». Пример из учебника «Логика»: Ст.125 УК РФ гласит: «Похищение чужого ребенка или подмена ребенка, совершенные с корыстной целью или из иных низменных побуждений наказываются…». Часть статьи «из иных низменных побуждений» говорит о неполноте дизъюнктивного перечисления признаков, т.к. конкретный вид побуждения решит суд, ибо перечислить все виды побуждений просто невозможно. Еще пример: «При заражении СПИДом сопротивляемость организма медленно, в течении многих месяцев и лет, снижается и приводит к возникновению различных заболеваний, прежде всего инфекционных, поражает легкие, органы пищеварения, кожу, нервную систему и т.д.». Здесь тоже невозможно перечислить все возможные поражения организма. Их установит врач при конкретном исследовании.
Условное (или импликативное – от лат. impricatio - сплетение) суждение. Это сложное суждение, формулируемое с помощью связки «если …, то …» и устанавливающее, что одно событие является основанием или условием другого события. Например, «Если фигура прямоугольник, то его диагонали равны», «Если студент усердно и систематически занимается изучением наук, то он получит глубокие знания», «Если говорят, что у тебя «золотые руки», то не следует бежать в ломбард». Условное суждение состоит из двух или более простых суждений. То суждение, которому предпослано слово «если», называется антецедент (от лат. antecedens - предшествующий) или основанием. Высказывание, идущее после слова «то», называют консеквентом (от лат. concequens - следствие). Высказывая условное суждение, мы имеем ввиду следующую мысль: если есть то, о чем говорится в основании условного суждения, то должно быть и то, о чем говорится в следствии.
В условном суждении истинность антецедента достаточна для признания истинности консеквента. Если антецедент обозначить буквой А, а консеквент – буквой В, а связь между ними знаком импликации «→» или « Среди условных суждений можно выделить следующие виды связей: 1) Суждения, отражающие причинные связи. Пример: «Если воду нагреть до 1000 С при нормальном давлении, то она закипит»; «Если Луна в новолуние находится в узле своей орбиты, то наступает солнечное затмение». 2) Суждения, отражающие связь логического следования между посылками и заключением правильного умозаключения, когда знание об одном факте является логическим основанием для утверждения знания о другом факте. Например: «Если все люди есть разумные существа и Петров человек, то он разумное существо»; «Если ртуть в термометре поднялась, то значит, в комнате стало теплее». (Нет причинной связи, но логическое следование есть). 3) Суждения, выражающие семантическую (т.е. обозначающую, выражающую значение слова) связь. Примером такой связи будет суждение: «Если Петр – муж, то он женат». 4) Суждения, выражающие такую связь, когда наличие одного факта есть условие для наличия другого факта. Например: «Если купим билеты, то мы пойдем в кино»; «Если завтра будет солнечная погода, то мы пойдем на пляж» (нет причинной связи). Условная связь может выражать также закон природы («Если камень подбросить вверх, то он упадет на Землю»), общественную закономерность («Если есть эксплуатация человека человеком, то не может быть равенства между людьми»), правила, этические нормы и т.д. Связь, которая выражается в условном суждении предполагает, что консеквент с необходимостью следует из антецедента, т.е. это говорит о том, что наблюдается здесь общий закон, сформулировав который, мы можем логически вывести консеквент из антецедента. Например, условное суждение «Если алюминий металл, то он электропроводен» предполагает общий закон, что «Все металлы электропроводны». Ввиду того, что антецедент условного суждения в совокупности с заключенной в нем информацией, содержательно определяет истинность консеквента, принято первую часть условного суждения называть основанием, а вторую – следствием. Связь между ними имеет два важных логических свойства: -1) истинность основания достаточна, чтобы признать истинность следствия; -2) ложность следствия с необходимостью указывает на ложность основания.
Логический союз «если, …то» определяется следующим образом: это такая связь двух суждений (образующих условное суждение), которое ложно, когда основание является истинным, а следствие ложным и условное суждение является истинным во всех остальных случаях, когда основание и следствие истинны; когда основание ложно, а следствие истинно; и когда основание и следствие ложны. Этот логический союз или связь называют в логике импликацией, а условные суждения импликативными. Условия истинности высказывания «Если А, то В» или «если p→q» можно дать в виде таблицы №5:
Таблица 5
Из таблицы видно, что импликация истинна во всех случаях, кроме одного, когда антецедент истинен, а консеквент ложен (2-я строка).
5) Эквиваленция – такая связь двух или более простых суждений, которая истинна тогда и только тогда, когда оба суждения истинны или ложны одновременно. «Р, если и только если q». «Треугольник является равносторонним, если и только если, он является равноугольным». «Этот ученый не завершит свою научную работу, если и только если (тогда и только, тогда) не будет своевременного финансирования его экспериментов».
Таблица 6
Из таблицы высказываний видно, что А и В эквивалентны, если и только если каждая из них необходима и достаточна для истинности другой формулы. Если истинна как прямая импликация (А→В), то истинна и ей обратная (В→А). Эквивалентные формулы, как видим, могут переставляться местами без потери смысла высказывания. Треугольник является равноугольным, если и только если он является равносторонним.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 797; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.216.248 (0.01 с.) |

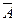 ). См. таблицу.
). См. таблицу. Союз «либо» («V») при строгой дизъюнкции имеет точку над символом и употребляется как разделительный. Составляющие строгую дизъюнкцию исходные суждения не могут быть одновременно истинными. Поэтому исключающе-разделительная дизъюнкция определяется как такая связь двух исходных суждений (образующих новое суждение), которое будет истинным лишь тогда, когда одно из них истинно, а другое ложно, и новое суждение будет ложным, если оба исходных суждения истинны или ложны. {Либо А либо В – А V В}.
Союз «либо» («V») при строгой дизъюнкции имеет точку над символом и употребляется как разделительный. Составляющие строгую дизъюнкцию исходные суждения не могут быть одновременно истинными. Поэтому исключающе-разделительная дизъюнкция определяется как такая связь двух исходных суждений (образующих новое суждение), которое будет истинным лишь тогда, когда одно из них истинно, а другое ложно, и новое суждение будет ложным, если оба исходных суждения истинны или ложны. {Либо А либо В – А V В}. Важнейшей функцией условного суждения является обоснование одного высказывания ссылкой на другое высказывание.
Важнейшей функцией условного суждения является обоснование одного высказывания ссылкой на другое высказывание. », то структура символической записи будет выражена формулой: «Если А, то В» [А→В] (есть другое обозначение: p→q; А
», то структура символической записи будет выражена формулой: «Если А, то В» [А→В] (есть другое обозначение: p→q; А 


