
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие доказательства: структура и видыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проблема доказательства и его приемы были и остаются предметом внимания логиков со времени зарождения логики, т.к. достижение достоверного, истинного знания связано с доказательством. Доказательство – это логическая операция, обосновывающая истинность какой-либо мысли с помощью других мыслей. Многовековой опыт убедил людей в том, что доказательность является важным свойством правильного мышления. Еще Аристотель говорил, что люди тогда всего более в чем-нибудь убеждаются, когда им представляется что, что-либо доказано. Цицерон говорил, что сила доказательств выше всякого авторитета. Всякое доказательство представляет свой вывод об истинности доказываемой мысли из других мыслей, признанных за истинные. Это предполагает решение двух задач: - 1) точно определить и правильно классифицировать формы отношений между мыслью доказываемой и мыслями, с помощью которых обосновывается истинность доказываемой мысли; Дело в том, что вопрос о том, какую истинную по содержанию мысль надо взять в качестве посылки доказательства, логика не может указать. В каждом конкретном случае это определяется той или иной наукой. Например, хорошо или плохо знает логику физик, но чтобы доказать истинность тезиса о том, что волновая функция есть статистическая характеристика квантового ансамбля, а не отдельной частицы – физику надо знать истинные мысли из других областей физики (квантовой механики), из которых можно вывести истинность доказываемого тезиса. Но вот вопрос о том, какую нужно взять мысль по форме – общее, частное или единичное суждение и какие логические формы связи и отношения использовать между известными истинами, взятыми в качестве доказательства и доказываемым тезисом - это решает логика. - 2) выяснить, какие мысли являются уже доказанными и истинными, которые мы берем в качестве доказательства. Если мы не найдем такие истинные мысли, а возьмем мысли, которые сами требуют доказательства, то этот процесс может быть долгим. Поэтому нужно брать такие истинные мысли, которые в обосновании не нуждаются. Несмотря на то, что каждая наука использует свои методы и факты, логика нашла то общее, что характерно для всех доказательств. Знание того общего, что лежит в основе связи и сочетания мыслей в процессе доказательства, позволило логике сформулировать структурные элементы доказательства и правила.
Общим для всех доказательств являются следующие элементы, образующие логическую последовательность: - 1) структура доказательства, - 2) способ доказательства, - 3) общие требования в отношении доказываемой мысли, - 4) и требования в отношении мыслей, с помощью которых обосновывается доказываемое положение. Структура доказательства. Всякое доказательство состоит из трех взаимосвязанных частей: тезиса; аргументов (доводов или оснований) и демонстрации. Структуру доказательства можно представить в виде след. схемы:
а1 а2... аn
Тезис (греч. слово – положение, утверждение) – это мысль или положение, истинность или ложность которого (выясняется) обосновывается в процессе доказательства. В качестве тезиса могут быть: - теоретическое положение науки, - теорема в математике, - результаты опытного исследования, которые нужно обобщить, - причина того или иного явления или события, - диагноз заболевания, - выяснение конкретного исторического факта и т.д. Доказательство будет успешным лишь в том случае, если доказываемый тезис истинен по своему содержанию. Аргументы. Доказательство осуществляется при помощи аргументов (доводов или оснований). Аргументы (лат. argumentum – логический довод, основание доказательства) – это истинные исходные теоретические или фактические положения, на которые опирается доказательство и из которых необходимо следует истинность доказываемого тезиса. Аргументами могут быть: аксиомы, принятые в данной научной системе, определения, суждения о достоверно известных фактах; теоретические или опытные обобщения и т.п. Так, при доказательстве некоторого суждения аргумент является основанием, из которого логически следует доказываемое суждение. Например, нам нужно доказать, что железо проводит электрический ток. Для этого достаточно двух аргументов: 1. «Все металлы проводят электрический ток. 2. Железо – металл».
Следовательно, железо проводит электрический ток.
Демонстрация – (от лат. demonstratio – показывание).
Истинность доказываемого тезиса не дана непосредственно, она не очевидна. Поэтому необходимо показать какова связь, которая ведет от истинности данных оснований к истинности тезиса. Эта связь требует выяснения. Положим, что ученик знает все определения, аксиомы и все теоремы, из истинности которых как из оснований выводится истинность теоремы Пифагора. Но это еще не значит, что он знает доказательство теоремы Пифагора. Чтобы знать доказательство необходимо: - знать какова связь между всеми основаниями теоремы Пифагора; - знать последовательность оснований и выводов из них, которая ведет к признанию истинности доказываемого в этой теореме положения.
Демонстрация отличается от тезиса и аргументов. Если тезис и аргументы могут быть представлены в виде отдельных суждений, то демонстрация – это более или менее длинная цепь суждений и умозаключений, посылками которых являются аргументы, а заключением – тезис. Продемонстрировать – это значит при помощи логических рассуждений доказать, что тезис логически следует из взятых нами аргументов по правилам соответствующих умозаключений. Обоснование тезиса может протекать в различной форме. Оно зависит от содержания и характера доказательства. Обоснование может иметь форму дедуктивных умозаключений, индуктивных умозаключений и умозаключений по аналогии. Виды доказательства. Различают прямое и косвенное доказательство. При прямом доказательстве истинность тезиса непосредственно обосновывается аргументами. Из аргументов а, в, с – с необходимостью следует доказываемый тезис d. Логическая формула прямого доказательства такова: 1) Из множества аргументов α выводим тезис β. 2) Множество аргументов α - истинно. 3) Тезис β - истинный
1. Все углеводы горючие 2. Сахар - углевод
Сахар - горюч
Косвенное (непрямое) доказательство. Здесь истинность выдвинутого тезиса обосновывается путем доказательства ложности антитезиса. Оно имеет два варианта: а) апагогическое (от греч. apagõg Допустим, что нам требуется доказать суждение А. Допускаем не-А, из него выводим следствие В, приводящее нас к противоречию. Следовательно, В является ложным. Тогда наше предположение, что из не-А следует В (не-А→В) может быть истинным только, если не-А является ложным. Следовательно А является истинным. Совершая переход от ложности не-А к истинности А, мы используем закон исключенного третьего. Разделительное доказательство. Это доказательство методом исключения. В этом доказательстве антитезис является одним из членов разделительного суждения, в котором нужно перечислить все возможные альтернативы. Например, нужно доказать, что проступок совершил Петров. Берем дизъюнктивное суждение: «Этот проступок совершил Иванов или Сидоров, или Петров». При доказательстве выясняется, что Иванов этот проступок не совершал, Сидоров также этот проступок не совершал. Их мы исключаем и получаем заключение: «Проступок совершил Петров».
Опровержение (лат. refutation – доказательство ложности или неправильности выдвинутых утверждений, предложений и доказательств). Обычно опровергают доказательства. Это более важный вид опровержения. Это можно сделать в отношении всех структурных элементов доказательства: - опровергнуть тезис; - опровергнуть аргументы; - опровергнуть способ доказательства. 1) Чтобы опровергнуть тезис, нужно доказать его ложность или доказать антитезис. Тезис: «все растения зеленые». Достаточно указать, что есть растения с розовыми листьями, желтыми, многоцветными. 2) Чтобы опровергнуть аргументы, мы используем тот же прием. Пример. «Земля имеет форму шара». Приводят аргумент: «Это доказывается кругосветным путешествием».
А К
3. Правила и ошибки в доказательстве. Значение этих правил в том, что они помогают твердо обосновывать наши знания; помогают разоблачать ложные приемы доказательства. Существуют след. правила доказательства: 1) доказываемый тезис должен быть определен ясно и четно; 2) в процессе доказательства нельзя подменять тезис; 3) используемые в доказательстве аргументы должны быть истинными; 4) аргументы должны быть достаточными для обоснования тезиса; 5) аргументы должны быть такими суждениями, истинность которых доказана независимо от тезиса; 6) тезисом должно быть такое выводное суждение, которое логически следует из аргументов. Тезис – это суждение логически следующее из аргументов. Эти правила ясны и понятны и не требуют особых комментариев. Но ложные приемы доказательства, играющие большую роль в таких науках как философия, политическая экономия, история, социология, психология и, особенно, в политической жизни и идеологии, следует рассмотреть. Здесь часто используются софизмы – вид ложного доказательства. Их цель – представить обманные утверждения как истинные, а истинные – как ложные. При ложном доказательстве речь идет не столько об ошибках, сколько об обманных приемах. Защищают ложный тезис при помощи ложного доказательства не потому, что не знают правил доказательства, а потому, что в этом заинтересованы.
Уже Аристотель знал об этом и сформулировал правила доказательства и указал почти все ошибки. Умение разоблачать ложные доказательства важно не потому, что это удержит софистов или лжецов, а потому, что оно научит нас разоблачать демагогов1, софистов, политических авантюристов и т.п. Типы ложного доказательства, встречающиеся в научных, идеологических и политических доказательствах:
1) Подмена доказываемого тезиса - это ошибка в доказательстве в результате нарушения закона тождества. Начав доказывать один тезис, в ходе доказательства переходят к доказательству другого тезиса, который внешне сходный с первым. Например, начав доказывать что-то несправедливое в моральном смысле, доказывают, что это несправедливо в юридическом смысле.
2) Доказательство через доказываемое, или круг в доказательстве (то же, через то же). Например, тезис А доказывается тезисом В и, одновременно В доказывается через А. Так, чтобы доказать тезис о том, что «человек разумное животное», ссылаются на то, что он может рассуждать, а рассуждать он может потому, что он разумен.
3) Учетверение термина. Это ошибка в умозаключении (в силлогизме). Известно, что в умозаключении должно быть три термина, а не четыре. Появление четвертого термина происходит от того, что употребляют многозначное слово. Пример:
1. Все металлы элементы 2. Латунь - металл
След., латунь - элемент
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 868; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.119.34 (0.013 с.) |

 тезис
тезис




 демонстрация
демонстрация аргумент
аргумент
 Таким образом, демонстрация – это логическая связь между аргументами и тезисом, выраженная в форме логического рассуждения, в ходе которого из аргументов выводится истинность тезиса.
Таким образом, демонстрация – это логическая связь между аргументами и тезисом, выраженная в форме логического рассуждения, в ходе которого из аргументов выводится истинность тезиса. .
. s – уводящий). – это доказательство, когда мы допускаем истинность противоречащего суждения, т.е. истинность антитезиса. Это так называемое доказательство от противного. При этом допускается временно истинность противоречащего суждения, из которого выводят следствия, в результате чего мы приходим к противоречию. На этом основании делается заключение, что противоречащее суждение ложно, и, следовательно, истинно доказываемое суждение.
s – уводящий). – это доказательство, когда мы допускаем истинность противоречащего суждения, т.е. истинность антитезиса. Это так называемое доказательство от противного. При этом допускается временно истинность противоречащего суждения, из которого выводят следствия, в результате чего мы приходим к противоречию. На этом основании делается заключение, что противоречащее суждение ложно, и, следовательно, истинно доказываемое суждение.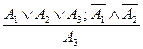














 Но! Этот аргумент сомнителен. Говорят, что выйдя из точки А и двигаясь по одному и тому же меридиану, можно вернуться к точке А. Но это можно сделать и тогда, когда Земля не круглая (см. рис.).
Но! Этот аргумент сомнителен. Говорят, что выйдя из точки А и двигаясь по одному и тому же меридиану, можно вернуться к точке А. Но это можно сделать и тогда, когда Земля не круглая (см. рис.).



