
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модальность суждений: понятие и видыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Модальность (от лат. modus – мера, способ) – это характеристика, оценка суждения, данная с той или иной точки зрения. Каждое суждение имеет основную информацию о том, какова связь предмета с его признаками. Но суждение в явном или неявном виде включает и дополнительную информацию о том, каков характер или тип связей отражен в суждении. Модальная оценка суждения выражается с помощью понятий: «необходимо», «возможно», «опровержимо», «разрешено» и т.п., т.е. модальных операторов (преобразователей). В суждении можно выразить мысль о предмете и его признаке, т.е. показать связь между S и Р. Но в суждении, сверх того, можно показать – является ли эта связь необходимой или случайной, всегда ли S будет Р или иногда, доказано ли, что S есть Р или только предполагается и т.д. В отличие от логики высказываний и логики предикатов, где два значения «и» и «л» в модальной логике может быть множество значений. Эти уточнения и будут выражать разные типы модальности, а суждения, в которых выражена модальность – будут модальными. В общей форме модальность суждения можно выразить с помощью модального оператора «М» и выразить модальность суждения символически: М (S есть/не есть Р). Вместо М можно подставлять различные оценочные понятия, которые будут выражать тип связи S и Р. Например, из немодального высказывания «Человек смертен», можно образовать модальные суждения: - «Плохо, что человек смертен», - «Возможно, человек смертен», - «Необходимо, что человек смертен», - «Доказано, что человек смертен» и т.д. Как видим, одно и то же суждение может стать объектом нескольких модальных оценок. Логические связи модальных высказываний изучает модальная логика. Итак, модальность суждения – эта выраженная в суждении дополнительная информация о характере обоснованности или о типе зависимости между S и Р, отражающая объективные отношения между предметами и их признаками. Термин «модальность» в логике употребляется в двух смыслах: в узком и широком. Такие свойства суждений как необходимость, действительность, возможность, случайность и т.п. называют модальностями в узком смысле. Эти модальности и есть модальности в собственном смысле слова, изучаемые традиционной логикой. В последнее время для их обозначения используют термин («алейтея») – алейтические модальности (от греч. слова «алейтея» - истина, необходимо). Это позволяет отличить модальности в собственном смысле слова от модальностей в широком смысле слова (Курбатов В.И. Логика. – Ростов н/Д – 2001 – гл.5.1. Алейтич. мод. логика). Модальности в широком смысле слова в современной логике разделены на классы. Например: - физическая модальность, - эпистемическая (от греч. слова «эпистеме» - знание или теоретико-познавательная), - деонтическая (от греч. слова «deon» - должное; раздел этики, рассматривающий проблемы долга), т.е. нормативная модальность, - аксиологическая (от греч. слова «axia» - ценность) – оценочная модальность, - временная и т.п. У нас нет возможности для их изучения. Мы ограничимся изучением основных (алейтических) модальностей, необходимости, действительности и возможности, поскольку это и есть модальности традиционной логики в собственном смысле слова. Рассмотрим их. Суждения необходимости (их называют аподиктическими, от лат. слова «apodiktikos» - достоверность). К необходимым относятся суждения, которые выражают научные законы, правила, аксиомы, положения, которые вытекают из других законов и аксиом и т.п., т.е. суждения, в которых достоверно твердо установлено знание о чем-то. Примеры: «Луна – спутник Земли», «Прямая линия – есть кратчайшее расстояние между двумя точками», «Человек относится к роду Гомо сапиенс» и т.п. Формула: «S необходимо есть (не есть) Р». Суждения действительности (или ассерторические от лат. «assero» - утверждаю). Это суждения, в которых (говорится), констатируется, утверждается о наличии или отсутствии у предмета того или иного признака. Например, «Шевченко получил сегодня отличную оценку»; «Байкал – самое глубокое озеро в мире»; «Лев Толстой родился в 1828 году». По качеству суждения действительности могут быть положительными и отрицательными. «Софийский собор в Киеве – выдающийся памятник архитектуры»; «Луна не имеет воздушной атмосферы». По количеству ассерторические суждения бывают единичными – «Киев столица Украины», частными – «Некоторые писатели лауреаты Нобелевской премии», общими - «Все студенты сдают экзамены». Хотя в суждениях действительности отражается принадлежность или непринадлежность признака предмету, но нам неизвестно, необходимо ли, т.е. всегда и при всех ли условиях, принадлежит данный признак предмету. Это значит, что суждения действительности мы используем в тех случаях, когда имеем сведения о принадлежности или непринадлежности данного признака предмету сейчас и в прошлом. Формула: S есть/не есть Р. Суждение возможности (проблематическое суждение) – такое, в котором отображается возможность наличия или отсутствия признака у данного предмета. Например, «Возможно в 2010г. будет хороший урожай зерновых», «Возможно футбольная команда «Шахтер» станет чемпионом и в будущем году». В этих суждениях утверждается лишь возможность чего-то. Но вполне возможно, что оно невозможно, т.е. «хорошего урожая не будет», а «футбольная команда «Шахтер» не станет чемпионом». По качеству суждения возможности являются утвердительными, а по количеству – могут быть единичными («Я не могу перепрыгнуть эту высоту»), частными («Некоторые студенты могут стать хорошими предпринимателями») и общими («Каждый студент может стать отличником»). Формула: «S возможно есть Р». Суждение возможности (по мнению Таванца П.В.) может употребляться в следующих двух случаях: 1) если известно, что данный признак проявляется в предмете при наличии одних условий и исчезает при наличии других условий, то знание об отношении этого признака к предмету вне наличия тех или иных условий выражается в суждении возможности; (например: при наличии таланта и других условий студент может стать хорошим предпринимателем); 2) если известно, что данный признак принадлежит только некоторым предметам известного рода, то знание о принадлежности этого признака любому предмету данного рода выражается в суждении возможности; (например: возможно, все студенты нашей группы станут хорошими специалистами). Таково самое общее представление о модальности суждений в традиционной логике. Сейчас появилось много различных толкований модальности суждений. Об иных видах модальности можно прочитать в рекомендованном списке литературы.
Тема 6: «Умозаключение».
1. Понятие об умозаключении, его структура и виды. 2. Дедуктивные умозаключения. 3. Индуктивное умозаключение и его виды. 4. Аналогия и ее виды.
Умозаключение – это третья форма рационального познания, осуществляемого в мышлении. Если понятие отражает общие признаки определенного класса предметов, а суждение – связь между понятиями, выражая его логическое значение, то умозаключение связывает воедино понятия и суждения и позволяет демонстрировать целостный процесс познания. Особенностью умозаключения является его выводной характер и использование предшествующих форм мышления.
1. Понятие об умозаключении, его структура и виды.
Умозаключение – это логическая форма получения выводного знания, которая состоит в переходе от определенных исходных данных к новому знанию, вытекающему из этих данных. Умозаключение имеет свою структуру, которая включает: 1) – непустое множество (двух или более) исходных суждений, называемых посылками (или основаниями); 2) – логический переход от посылок к заключению, называемому выводом; 3) – новое суждение, несущее новое знание, полученное логическим путем из посылок, называемое заключением (или следствием). Всякое умозаключение будет правильным при выполнении следующего требования: 1) если посылки умозаключения истинны, то должно быть истинно и заключение. Это требование достигается; 2) если умозаключение построено по законам и правилам логики. Соблюдение этих законов и правил называют логическим с л е д о в а н и е м заключения из исходных данных умозаключения. Например: Все жидкости упруги Вода – жидкость Вода упруга. и еще: А равно В В равно С Следовательно, А равно С. В этих умозаключениях п о с ы л к а м и соответственно являются суждения: «Все жидкости упруги», «Вода - жидкость» - в первом; «А равно В», В равно С – во втором. П р а в и л о м – положение «Если все жидкости обладают признаком упругости, а вода относится к классу жидкостей, то она также обладает признаком упругости» (1). «Если два предмета равны в каком-либо отношении третьему, то они равны в этом же отношении и между собою» (2). В ы в о д о м - суждения: «Вода упруга» и «А равно С». Вывод дает нам новое знание, которого не было в посылках. Новизна выводного знания в различных умозаключениях имеет различный характер. 1. По характеру выводного знания и в зависимости от строгости правил вывода в логике выделяют два вида умозаключений: 1) – необходимые умозаключения (демонстративные); 2) – правдоподобные – вероятные (недемонстративные). В необходимых умозаключениях заключение следует из посылок с необходимостью.
Например: Все металлы электропроводны Железо – металл Следовательно, железо электропроводно. В вероятных умозаключениях мы получаем лишь вероятное знание. Например: «Планета Марс сходна с Землею по многим признакам. На Марсе есть атмосфера, вода, температура воздуха близка к температуре воздуха на Земле и т.д. На Земле есть органическая жизнь». Вероятно, и на Марсе есть органическая жизнь. По характеру направленности логического следования (в логике) дается классификация умозаключений, которая определяется тем, какая степень знаний выражена в посылках и заключении. В соответствии с этим умозаключения делятся на дедуктивные, индуктивные и умозаключения по аналогии. Рассмотрим их.
II. Д е д у к т и в н ы е умозаключения
Дедукция – слово лат. deduction – выведение. Дедуктивным называется такое умозаключение, в котором вывод идет от общего знания к частному. Например: Все рыбы дышат жабрами. Осетр – рыба. Осетр дышит жабрами.
Все люди смертны. Сократ – человек. Сократ смертен. По количеству посылок дедуктивные умозаключения делятся на н е п о с р е д с т в е н н ы е и о п о с р е д с т в о в а н н ы е. Непосредственным называют умозаключение, в котором вывод делается только из одной посылки. Например: Все химические элементы простые вещества. Следовательно, ни одно сложное вещество не является химическим элементом. Опосредственным называется умозаключение, в котором вывод делается из нескольких посылок. Например: Все деревья растения. Береза – дерево. Береза – растение. Рассмотрим непосредственные умозаключения подробнее. В дедуктивном суждении отображены общие отношения между предметами и их свойствами (отношения тождества, различия, противоположности, противоречия и т.п.). Эти отношения составляют общий смысл различных конкретных суждений. Причем, эти отношения в суждениях взаимосвязаны так, что непосредственное утверждение одного из них есть косвенное, неявное утверждение и другого. Непосредственное умозаключение и дает нам возможность выявить эти другие стороны суждений, сделать явным и тем самым получить новое знание. Это новое знание можно получить также путем преобразования суждения. При преобразовании меняется функция суждения. Исходное суждение рассматривается как посылка, а новое суждение, полученное в результате преобразования – как заключение. Умозаключение, полученное путем преобразования и называется н е п о с р е д с т в е н н ы м. Таких преобразований четыре: - превращение, - обращение, - противопоставление предикату, - умозаключение по логическому квадрату. 1) Превращение суждений. Превращение состоит в том, что из данного суждения получаем равнозначное ему суждение, но противоположное по качеству, т.е. из утвердительного суждения получаем равнозначное отрицательное и наоборот. Формально прием превращения суждений состоит в том, что мы изменяем связку исходного суждения на противоположную и заменяем предикат этого суждения противоречащим понятием. Так, из суждения «S есть Р» получаем суждение «S не есть не-Р». Например: «Человек есть разумное существо». Превращаем и получаем «Человек не есть не разумное существо» или «Все металлы суть химические элементы» - «Ни один металл не есть не химический элемент». Операция превращения всегда приводит к истинному результату, если исходное суждение было истинным. Превращать можно любые категорические суждения: А,Е, I, О. О б щ е у т в е р д и т е л ь н о е суждение превращается в общеотрицательное. «Все цветы суть растения» → «Ни один цветок не есть не растение». Схема превращения суждения А:
О б щ е о т р и ц а т е л ь н о е суждение превращается в общеутвердительное. «Ни одна планета не светит собственным светом» → «Все планеты светят не собственным светом» (т.е. они светят отраженным светом). Схема превращения суждения Е:
Частоутвердительное суждение I превращается в частоотрицательное – (О). Например: «Некоторые животные являются млекопитающими» → «Некоторые животные не являются немлекопитающими».
Схема превращения суждения I:
Частоотрицательное суждение О превращается в частоутвердительное I. Например: «Некоторые студенты не являются отличниками» → «Некоторые студенты являются неотличниками».
Схема превращения суждения О:
В чем же смысл и значение превращения? Оно в следующем. а) Превращение не дает в выводном суждении существенно нового, но уточняет наши знания. В практике мышления превращение используют в следующих целях: - как составную часть более сложных и опосредствованных суждений; - когда нам важно в утвердительном суждении выявить отношение различия, а в отрицательном – отношение тождества, чтобы в определенных целях уточнить нашу мысль. Иногда различные оттенки мысли имеют существенное значение для достижения точности мышления. б) В результате превращения мы рассматриваем предмет суждения с новой стороны и обнаруживаем, что предмет не может обладать и в то же время не обладать одним и тем же признаком. в) Из выводного знания, полученного в результате превращения, можно снова получить исходное суждение. Эта особенность превращения суждений выражается в правиле – двойное отрицание чего-либо равносильно утверждению того же самого. Например, возьмем отрицательное суждение «Кит не есть не млекопитающее» и превратим его в утвердительное. Получим: «Кит есть не не млекопитающее», в котором в предикате два отрицания. Они равносильны утверждению «Кит есть млекопитающее».
2) Обращение. Обращение – такое непосредственное умозаключение, в котором в заключении субъектом становится предикат, а предикатом – субъект суждения, т.е. S и Р меняются местами, при этом качество суждения сохраняется. Схема обращения:
Различают два вида обращения – чистое (или простое) и обращение с ограничением. Они различаются по следующему признаку. В чистом обращении количество суждения не меняется. А это бывает тогда, когда S и Р исходного суждения либо оба распределены, либо оба не распределены. Примеры: «Все студенты – учащиеся вуза». При обращении имеем: «Все учащиеся вуза - студенты» (суждение А). (Суждение J): «Некоторые студенты - спортсмены» - «Некоторые спортсмены - студенты». Для обращения с ограничением характерно изменение количества суждения, т.е. кванторное слово «все» меняется на «некоторые» и наоборот. Примеры: «Все студенты - учащиеся» - обращается в «Некоторые учащиеся - студенты». «Некоторые юристы - адвокаты» - «Все адвокаты - юристы». Из всех видов суждений А, Е, J, О суждение О – частоотрицательное не обращается.
3) Противопоставление предикату. Это такое непосредственное умозаключение, когда субъект исходного суждения становится предикатом, а предикат становится субъектом с отрицанием «не», а связка меняется на противоположную.
S есть Р Схема обращения: не-Р не есть S
Противопоставление предикату – это по сути результат двух последовательных непосредственных умозаключений при превращении и обращении суждений. Умозаключение для различных видов суждений рассмотрим на примерах. - Суждения вида А (общеутвердительные) – все S есть Р – Ни одно не – Р не есть S: «Все студенты - учащиеся» - «Ни один не учащийся не является студентом». - Суждения вида Е (общеотрицательные) – Ни одно S не есть Р – Некоторые не Р есть S: «Ни одна планета не светит собственным светом» - «Некоторые не светящие собственным светом являются планетами». - Суждения вида О (частоотрицательные) – «Некоторые S не есть Р» - «Некоторые не Р есть S»: «некоторые студенты не являются спортсменами» - «Некоторые не спортсмены являются студентами». - Суждения вида J (частоутвердительные) – не дают непосредственного умозаключения.
4) Умозаключение по логическому квадрату.
А П р о т и в о п ол о ж н ы е Е
о о
ч ч
J с у б к о н т р а р н ы е O
Получаем формулы: Все S есть Р – Некоторые S есть Р. Пример: из суждения «Все студенты группы А - отличники» получаем «Некоторые студенты группы А - отличники». Из «Ни одно S не есть Р» получаем «Некоторые S не есть Р». «Если ни один студент группы Б не имеет академической задолженности, то некоторые студенты этой группы также не имеют академической задолженности». Противоречащие суждения А – О и Е – J дают такие умозаключения, что если одно из них истинно, то другое – ложно, т.е. подчиняются закону исключенного третьего, с которым вы уже хорошо знакомы. Возьмем два противоречащих суждения А - О: «Все деревья - растения» и «Некоторые деревья – не растения». Если истинно суждение «Все деревья - растения», то суждение «Некоторые деревья – не растения» - ложно. Аналогично и с суждениями Е – J.
Силлогизм (простой категорический силлогизм). Состав силлогизма.
Силлогизм (от греч syllogismos) – сосчитывание. Силлогизм – это опосредствованное умозаключение, т.к. вывод в нем делается из двух посылок. Всякий силлогизм есть умозаключение достоверности. Если посылки силлогизма истинны и соблюдены правила вывода, то всегда получим истинное заключение. В качестве посылок и заключения в силлогизм могут входить любые суждения. Например: В силлогизме: 1. Каждое А больше В. 2. Х есть А. 3. Следовательно, Х больше В – одна из посылок и заключение – простые суждения отношения.
В силлогизме: 1. Все металлы электропроводны и теплопроводны. 2. Алюминий металл. 3. Следовательно, алюминий электропроводен и теплопроводен – одна из посылок и заключение – соединительные суждения.
В силлогизме: 1. Каждое дерево является либо хвойным, либо широколиственным. 2. Данное растение – дерево. 3. Следовательно, данное растение либо широколиственное, либо хвойное дерево. Одна из посылок и заключение – разделительные суждения.
А в силлогизме: 1. Всякая жидкость превращается в пар, если ее нагреть до определенной температуры. 2. Вода – жидкость. Следовательно, вода превращается в пар, если ее нагреть до определенной температуры. Одна из посылок и заключение – условные суждения. Несмотря на различные виды суждений, приведенных здесь, особенностью силлогизма является то, что все входящие в состав силлогизма суждения рассматриваются здесь как суждения, в которых утверждается или отрицается принадлежность признака предмету или как тождество, или различие каких-либо предметов. По этой причине в силлогизме, независимо от его логической формы, все суждения рассматриваются как простые категорические суждения принадлежности. Понятия, входящие в силлогизм, называются т е р м и н а м и. В каждом силлогизме имеется три термина. Возьмем силлогизм: 1. Все люди – смертны. 2. Сократ – человек. Следовательно, Сократ смертен. В этом силлогизме терминами являются: «Люди», «Смертны», «Сократ». Каждый термин имеет свое название. Термин, который в заключении выступает как S, называют м е н ь ш и м термином – (в нашем примере – «Сократ»). Обозначается буквой «S». Термин, который является предикатом заключения называют б о л ь ш и м термином – (в нашем примере – «Смертен»). Обозначается буквой «Р». Больший и меньший термины называют крайними терминами. Термин, входящий в обе посылки и отсутствующий в заключении («люди») называется средним термином и обозначается буквой М (от латинского слова «medius»-средний). Роль среднего термина в том, что он связывает между собой больший и меньший термины. Посылка, включающая больший термин, называется большей посылкой – (Все люди (М) – смертны (Р)). Посылка, включающая меньший термин, называется меньшей посылкой («Сократ (S) – человек (М)»). Формула этого силлогизма такова: Все (S) М суть Р. S есть (Р) М, следовательно S есть Р. Сказанное дает основание для определения силлогизма. Силлогизмом называется умозаключение, устанавливающее связь между крайними терминами в заключении на основании их отношения к среднему термину в посылках.
Аксиома силлогизма.
А к с и о м а (от греч. axioma – значимое, достойное уважения, бесспорное) – исходное положение какой-либо теории, лежащее в основе доказательств других положений этой теории, в пределах которой оно принимается без доказательства. А к с и о м а с и л л о г и з м а – это такое положение, которое позволяет сделать логический переход от посылок к заключению. В логике используют две аксиомы: объемную и атрибутивную. О б ъ е м н а я а к с и о м а формулируется так: «Все, что утверждается или отрицается относительно всех предметов данного класса, утверждается или отрицается относительно любой части или каждого предмета этого класса». Если нам известно, что каждый предмет класса А обладает свойством Р, то это значит, что любой предмет, относящийся к классу А обладает свойством Р. И наоборот: если каждый предмет класса А не обладает свойством Р, то и любой предмет, относящийся к классу А не обладает свойством Р. Так, если нам известно, что любая жидкость обладает признаком упругости (Р), то выяснив, что нефть относится к классу жидкостей, мы можем утверждать, что и нефть обладает этим свойством. Это рассуждение можно сформулировать в виде силлогизма:
1. Все жидкости (М) упруги (Р). 2. Нефть (S) – жидкость (М). Следовательно, нефть (S) упруга (Р).
О б ъ е м н о е т о л к о в а н и е а к с и о м ы позволяет нам изобразить отношение между терминами силлогизма, в круговых схемах Эйлера-Венна. Т.е., отношения между терминами силлогизма можно представить как отношения объемов соответствующих понятий: S M P.
Если объем понятия М входит в объем
входить в объем понятия Р.
А т р и б у т и в н а я ф о р м у л и р о в к а а к с и о м ы выражает связь между предметом и его признаком и определяется так: если данной вещи присущ какой-то признак, а этому признаку в свою очередь присущ другой признак, то этот второй признак является также признаком вещи. Или: признак признака есть признак вещи. Например: 1. Все растения (М) имеют корневую систему (Р). 2. Ромашка (S) – растение (М). Следовательно, ромашка (S) имеет корневую систему (Р).
Если «корневая система» (Р) – признак «всех растений» (М), а (М) – «быть растением» является признаком ромашки (S), то Р (признак «иметь корневую систему») – есть признак ромашки, т.е. Р выступает как признак признака М предмета S (ромашка). Это видно из заключения S – Р. Как видим, в основе силлогических умозаключений лежит совместимость или несовместимость свойств предметов и соответственно с этим объединение или разъединение предметов или классов предметов: - предметы, обладающие свойством Р, объединяются в один класс; - предметы же, обладающие разными свойствами (Р и не Р) распределяются по различным классам. В зависимости от того, тождественны или различны предметы двух классов, они полностью или частично включаются один в другой или исключаются один из другого. Если классы равночисленны и их предметы обладают одними и теми же свойствами, то они сливаются друг с другом, т.е. их объемы совпадают. Например: «Самая большая река Украины» и «река, имеющая своим притоком Припять». Эти очевидные положения, которые позволяют устанавливать совместимость или несовместимость двух классов, лежат в основе формулировок силлогизма.
Правила и фигуры силлогизма.
Мы выяснили, что силлогизм устанавливает совместимость или несовместимость двух классов предметов посредством среднего термина, в основе которых лежит аксиома силлогизма. Но, производя операции умозаключения, важно выяснить еще три обстоятельства: 1) какие формы истинных посылок с необходимостью дают истинное заключение; 2) какую форму суждения в каждом отдельном случае будет принимать заключение; 3) каким условиям должен удовлетворять средний термин, чтобы из истинных посылок с необходимостью получить истинное заключение. При этом мы будем иметь ввиду, что правила силлогизма распространяются на те силлогизмы, у которых посылки имеют вид А, Е, I, О и представляют собой суждения принадлежности.1 Общих правил категорического силлогизма 7: три правила относятся к терминам, а четыре – к посылкам. Правила терминов: 1-е правило – в силлогизме должно быть только три термина. Это означает, что средний термин, связывающий крайние термины в заключении, должен быть одним и тем же в обеих посылках, обозначать одни и те же предметы и иметь один и тот же объем. Это правило может быть нарушено из-за того, что одно и то же слово по своему написанию или звучанию может иметь различные значения и обозначать различные предметы. В этом случае, по сути, в силлогизме нет среднего термина, и мы имеем два различных понятия, выраженные одним словом.
______________________________ 1. Суждение принадлежности – в котором утверждается (или отрицается), что какой-либо признак принадлежит предмету известного рода, но не известно, принадлежит ли он и другим предметам или только данному. Эта ошибка есть результат нарушения требований закона тождества, и называется учетверением терминов. Пример: Все вулканы – горы. Все гейзеры – вулканы. Следовательно, все гейзеры – горы. Здесь четыре термина, а не три, т.к. слово «вулканы» употреблено в различных смыслах: в первой посылке «вулкан» - это огнедышащая гора, во второй – извержение, исходящее из глубин земли. И в результате получим ложное умозаключение. 2-е правило – средний термин должен быть распределен хотя бы в одной из посылок. Возьмем пример: 1. Некоторые студенты нашей группы отличники. 2. Кравченко – студент нашей группы. Кравченко – отличник. Но этот вывод ошибочен, т.к. средний термин «студенты нашей группы» в первой посылке не распределен, ибо взят не в полном объеме и поэтому невозможно сделать вывод о каждом студенте группы, что он отличник. Мы видим, что средний термин не связывает крайние термины. Если бы мы в первой посылке сказали: «все студенты нашей группы отличники», то вывод следовал бы с необходимостью. 3-е правило – термин, не распределенный в посылке, не может быть распределен и в заключении. Возьмем пример: 1. Все студенты должны иметь среднее образование. 2. Ткаченко – не студент. Следовательно, Ткаченко не должен иметь среднее образование. Вывод, как видим, неверный. Ибо среднее образование должны иметь не только студенты. В чем ошибка? Ошибка в большей посылке – в термине «среднее образование». Он взят не в полном объеме, т.е. не распределен. Среднее образование должны иметь все люди, а не только студенты. В посылке мы говорим, о части (группе) людей, а в заключении термин «среднее образование» взяли в полном объеме. Отсюда ошибка.
Правила посылок: 1-е правило: Из двух частных посылок нельзя сделать никакого вывода. Хотя бы одна из посылок должна быть общим суждением. Пример: 1. Некоторые отличники, закончившие ВУЗ, получили дипломы с отличием. 2. Некоторые студенты нашего вуза – отличники. Некоторые студенты нашего института, закончив ВУЗ, получили дипломы с отличием. Заключение ошибочно. Не все отличники, окончив ВУЗ, получают дипломы с отличием. 2-е правило: Из двух отрицательных посылок невозможно сделать заключение, хотя бы одна из посылок должна быть утвердительным суждением. Пример: Ни одна планета не светит собственным светом. Комета – не планета. Мы видим, что в первой посылке из объема среднего термина исключаются все тела, светящие собственным светом, а из второй посылки – то, что из объема среднего термина исключаются все кометы. Т.о., ни одно тело, светящее собственным светом, и ни одна комета не могут быть занесены в класс планет. И установить связь между телами, светящими собственным светом и кометами мы не в состоянии, т.к. не знаем, совпадают ли их объемы или нет. Поэтому из таких посылок сделать вывод невозможно. Хотя бы одна из посылок должна быть утвердительным суждением. 3-е правило: Из двух посылок, если одна из посылок – отрицательное суждение, то и заключение должно быть отрицательным. Пример: 1. Все студенты нашего института не изучают астрофизику. 2. Иванов – студент нашего института. Иванов не изучает астрофизику. Вывод отрицателен, т.к. средний термин разъединяет крайние термины. 4-е правило: Если одна из посылок – частное суждение, то и заключение должно быть частным. Пример: Все рыбы дышат жабрами. Некоторые водные животные – рыбы. Следовательно, некоторые водные животные дышат жабрами. Будет ошибкой сказать, что все водные животные дышат жабрами. Фигуры и модусы силлогизма.
Фигура силлогизма – это наглядная форма силлогизма, определяющаяся положением с р е д н е г о термина. Фигура силлогизма – это не игра ума, она отображает объективные связи между предметами и явлениями материального мира: связь между родом и видом, между видами, между видом и отдельным предметом. В зависимости от положения среднего термина получаются четыре фигуры силлогизма: 1) в первой фигуре средний термин является S-ом в большей посылке и Р-ом в меньшей:
1. Все студенты сдают экзамены. 2. Шевченко Николай – студент. Следовательно, Шевченко Н. сдает экзамены. S_ _ _ _ _ _ _ _ _ _ _ М
2) во второй фигуре средний термин является Р-ом в обеих посылках:
1. Все жидкости упруги. 2. Воск не упруг. Следовательно, воск не жидкость. S_ _ _ _ _ _ _ _ _ _ _ М
3) в третьей фигуре средний термин является S-ом в обеих посылках:
1. Все киты – млекопитающие. 2. Все киты – водные животные. Следовательно, некоторые водные животные - М_ _ _ _ _ _ _ _ _ _ S млекопитающие.
4) в четвертой фигуре средний термин является Р-ом в большей посылке и S-ом в меньшей.
Р_ _ _ _ _ _ _ _ _ _ М 1. 2. Ни одно млекопитающее не есть рыба. Ни одна рыба не есть кит. М_ _ _ _ _ _ _ _ _ _S
Наклонные и вертикальные линии фигур силлогизма обозначают связь между посылками, осуществляемую посредством среднего термина, а горизонтальные – связь терминов в посылках. Буква «М» - средний термин, «S» - меньший термин, «Р» - больший термин.
Практическое значение фигур силлогизма в том, что каждая фигура отображает различные приемы оперирования посылками.
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.012 с.) |



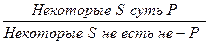





 д д
д д
 и и
и и н н
н н
 понятия Р, а объем понятия S входит в объем
понятия Р, а объем понятия S входит в объем понятия М, то объем понятия S необходимо будет
понятия М, то объем понятия S необходимо будет М_ _ _ _ _ _ _ _ _ _ _ Р
М_ _ _ _ _ _ _ _ _ _ _ Р Р_ _ _ _ _ _ _ _ _ _ _ М
Р_ _ _ _ _ _ _ _ _ _ _ М Все киты – млекопитающие.
Все киты – млекопитающие.


