
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление суждений по модальностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В логике мы до сих пор рассматривали простые суждения, которые называются ассерторическими, а также сложные суждения, составленные из простых. В них утверждается или отрицается наличие определенных связей между предметом и его свойствами или констатируется отношение между двумя или большим числом предметов. Например, «Школьники — учащиеся»; «Объем конуса равен 1/3 площади основания, умноженной на высоту»; «Яблоко сладкое и красное»; «Я эту работу не выполню в срок»; «Если будет плохая погода, то мы не поедем на теплоходе» и др. Общая форма таких простых высказываний (суждений): «5 есть (не есть) Р». Из простых суждений образуются сложные. Например, «Если S есть (не есть) Р, то S 1 есть (не есть) P 1». В этих ассерторических суждениях не установлен характер связи между субъектом и предикатом. Характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном суждении раскрывается в модальном суждении. Из вышеприведенных суждений можно образовать такие, например, модальные суждения: «Несомненно, что все школьники — учащиеся», «Доказано, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы», «Хорошо, что яблоко сладкое и красное», «Возможно, что я эту работу не выполню в срок», «Вероятно, что если будет плохая погода, то мы не поедем на теплоходе». Мы видим, что модальные суждения не просто утверждают или отрицают некоторые связи, а дают оценку этих связей с какой-то точки зрения. О предмете А можно просто сказать, что он имеет свойство В (это будет ассерторическое суждение). Но можно сверх того уточнить, является ли эта связь А и В необходимой или, наоборот, случайной; хорошо ли, что А есть В или это плохо; доказано, что А есть В или не доказано, а только есть предположение, и т. д. В результате таких уточнений мы получаем модальные суждения различных типов. Приведем другие примеры модальных суждений: «Возможно, на Марсе есть жизнь», «Доказано, что в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы, т. е. а2 + b2=с2»; «При красном свете светофора проезд транспорта запрещен» и др. В модальном суждении к ассерторическому суждению приписывается тот или иной модальный оператор (модальное понятие): возможно, доказано, необходимо, запрещено, обязательно, плохо и др.Структура простых модальных суждений такая: М (S есть Р) или М (S не есть Р), где М обозначает модальный оператор (модальное понятие). Но как было уже сказано, модальными могут быть и сложные суждения. Если а и b — простые суждения, то из сложных ассерторических суждений: aÙb, aÚb, aÚ×b, a®b, aºb — можно получить соответствующие сложные модальные суждения: M (aÙb); M (aÚb); M (aÚ×b); M (a®b); M (aºb).
В каждую из групп модальностей входят три основных модальных понятия. Второе из них называется слабой характеристикой, первое и третье — соответственно сильной положительной и сильной отрицательной характеристиками. Иногда в дополнение к трем основным модальным понятиям вводится четвертое, которое может употребляться для обозначения объединения сильного положительного и нейтрального. Логические и онтологические модальности объединяются вобщий вид — алетические модальности14. Они включают такие модальные операторы или категории модальности: необходимость и случайность, возможность и невозможность. Слова «необходимо», «возможно», «случайно» в обыденном языке употребляются в самых различных смыслах. Диалектико-материалистическая философия изучает категории «необходимость», «случайность», «возможность» и другие с их содержательной стороны. Формальная логика изучает существующие между ними формальные зависимости. Всеобщность модальных категорий состоит в их приложимости к любой области действительности. Алетические модальности обозначаются так: «ÿ А» — «необходимо А»; «Ñ А» — «случайно Л»; «◊ А» — «возможно А» ;x~◊A — «невозможно А»(знак «~»обозначает отрицание). Иногда их обозначают так: «Lp»— «необходимо р», «Мр»— «возможно». Алетические модальности (логические и онтологические) часто содержательно истолковывают так: необходимыми считают логические законы, а также законы, выявленные различными науками (естественными, математическими, общественными и техническими), и все следствия из этих законов. Невозможными считают суждения, противоречащие этим законам, отрицания этих законов или их следствий. Случайными считают суждения, не являющиеся законами или их следствиями, но и не противоречащие законам или их следствиям. Возможными считают сложения, не противоречащие законам или их следствиям.Взаимосвязь алетических модальностей Некоторые алетическне модальности в ряде систем можно определять одну через другую («=» обозначает «равно по определению», «Ù»— конъюнкцию, «Ú» —дизъюнкцию, «~» отрицание, ««»— эквивалентно, «®» — импликацию). Например, 1А= Некоторые важные связи, характеризующие алетические модальности, выражены следующими формулами: (1) (2) (3)
(4)
Задачи к теме «Суждение» I.Являются ли следующие формулы законами логики: 1) 2) 3) 4) 5) II. Определить вид суждения, его термины и их распределенность в следующих суждениях: 1. Иногда люди опаздывают на работу. 2. Все распространенные предложения имеют второстепенные члены. 3. Некоторые спортсмены не являются мастерами спорта. 4. Вода, нагретая до 80°С, не кипит. 5. Цыплят по осени считают. 6. Общественное бытие определяет общественное сознание. 7. Ни один учитель нашей школы не является отличником народного просвещения. 8. «Некоторые лекарства опаснее самих болезней» (Сенека). 9. «Никакая причина не извиняет невежливость» (Т. Г. Шевченко). 10. Среда — третий день недели. 11. Некоторые люди не изучают логику. III. Определить вид и логическую форму следующих сложных высказываний. Записать их структуру в виде формулы: 1. Покрылись зеленью сопки, освобождаются от снега вулканы, в скверы, на улицы Петропавловска-Камчатского в июне высажены деревья, кустарники, готовятся клумбы под цветы. 2. Этот приезд не является ни необходимым, ни желательным. 3. Поиски врага длились уже три часа, но результатов не было, притаившийся враг ничем себя не выдавал. 4. Если эта фигура квадрат, то диагонали в ней равны, взаимно перпендикулярны и в точке пересечения делятся пополам. 5. «Если вы желаете себе несокрушимого памятника, вложите свою душу в хорошую книгу» (Б. Буаст). IV. Произвести отрицание следующих сложных суждений, предварительно записав в виде формулы их структуру. 1. Если мне дадут отпуск летом, то я поеду отдыхать к морю или по туристической путевке в Карпаты. 2. Неверно, что этот писатель — драматург или поэт. V. Определить с помощью «логического квадрата» отношения между следующими простыми суждениями: 1. Неверно, что все дети послушны — Некоторые дети являются послушными. 2. Все книги — рукописные — Ни одна книга не является рукописной. VI. Определить вид модальности в следующих суждениях: 1. С появлением средств генной инженерии можно предвидеть значительные успехи в улучшении качества и состава микробиологической продукции. 2. Вероятно, молоко было одним из первых продуктов сельского хозяйства. 3. Хлебопечение возникло на заре развития человечества, вероятно, в Египте. 4. Необходимо соблюдать правила поведения в общественных местах. 5. Разрешен проезд автомобилей при зеленом свете светофора. 6. Невозможно построить вечный двигатель. 7. «Никогда не беспокой другого тем, что ты можешь сам сделать» (Л. Н. Толстой). 8. «В специально оборудованных вольерах для содержания горилл в зоопарках должны быть деревья, по которым они могли бы лазать, а также солома, ветки или бамбук для сооружения гнезд. Пищу следует давать небольшими порциями на протяжении всего дня, причем в таком виде, чтобы животные имели возможность заниматься ее подготовкой (скажем, обдирать кожицу или расщеплять стебли) или поиском, для чего лучше беспорядочно разбрасывать съедобные растения в вольере. Гориллам нужно обеспечить возможность пребывания на свежем воздухе» (курсив наш. — А. Г.) (Дайан Фосси). VII. Являются ли суждениями следующие предложения:1. «Что без тебя просторный этот свет? Ты в нем одна. Другого счастья нет». (В. Шекспир). 2. В каком году родился писатель А. Толстой? 3. Принеси мне книгу в среду вечером. 4. Не в свои сани не садись. 5. «Кто не проклинал станционных смотрителей, кто с ними не бранился?» (А. С. Пушкин). 6. «Каких цветов в саду весеннем нет!» (В. Шекспир). 7. «И казалось, что после конца Никогда ничего не бывает... Кто же бродит опять у крыльца И по имени нас окликает? Кто приник к ледяному стеклу И рукою, как веткою, машет?» (А. Ахматова).
Глава IV ОСНОВНЫЕ ЗАКОНЫ (ПРИНЦИПЫ) ПРАВИЛЬНОГО МЫШЛЕНИЯ ПОНЯТИЕ О ЛОГИЧЕСКОМ ЗАКОНЕ Фундамент материалистической диалектики — наиболее глубокого и всестороннего учения о развитии — составляют основные законы: закон взаимного перехода количественных и качественных изменений, закон единства и борьбы противоположностей и закон отрицания отрицания. Эти законы являются всеобщими: они действуют в природе, обществе и мышлении. Кроме них в объективном мире действует много других законов, изучаемых конкретными науками (физикой, химией, биологией и др.); существуют и общенаучные законы (например, закон сохранения энергии). Закон мышления — это необходимая, существенная, устойчивая, повторяющаяся связь между мыслями. Наиболее простые и необходимые связи между мыслями выражаются в основных формально-логических законах. К ним относятся законы тождества, непротиворечия, исключенного третьего, достаточного основания. Эти законы являются основными потому, что в логике они играют особо важную роль, являются наиболее общими, лежат в основе различных логических операций с понятиями, суждениями и используются в ходе умозаключений и доказательств. Первые три закона были выявлены и сформулированы Аристотелем. Эти законы можно выразить в виде формул математической (символической) логики. Закон достаточного основания был сформулирован Лейбницем. Основные законы логики являются отражением в сознании человека определенных отношений между предметами объективного мира. Формально-логические законы не могут быть отменены или заменены другими. Они имеют общечеловеческий характер: они едины для людей всех рас, наций, классов, профессий. Эти законы сложились в результате многовековой практики человеческого познания при отражении таких обычных свойств вещей, как их устойчивость, определенность, несовместимость в одном и том же предмете одновременно наличия и отсутствия одних и тех же признаков. Законы логики — это законы правильного мышления, а не законы самих вещей и явлений мира. Кроме четырех основных формально-логических законов, отражающих важные свойства правильного мышления — определенность, непротиворечивость, обоснованность, четкость мышления, выбор «или — или» в определенных «жестких» ситуациях, — существует много неосновных формально-логических законов, которым должно подчиняться правильное мышление в процессе оперирования его отдельными формами (понятиями, суждениями, умозаключениями). Законы логики, как основные, так и неосновные, функционируют в мышлении в качестве принципов правильного рассуждения в ходе доказательства истинных суждений и теорий и опровержения ложных суждений. В математической логике несколько иной подход. Там законы, выраженные в виде формул, выступают как тождественно-истинные высказывания. Это означает, что формулы, в которых выражены логические законы, истинны при любых значениях их переменных. Среди тождественно-истинных формул особо выделяются такие, которые содержат одну переменную. Схемы этих законов:
— закон непротиворечия. — закон исключенного третьего. Связь логических критериев истинности знания с практической деятельностью человека Не во всех науках критерий практики действует непосредственно. Следует подчеркнуть сложный, опосредованный характер отражения действительности в логических системах и их операциях, в логических формах и законах. Соотношение критерия практики с логическим критерием истинности заключений в умозаключении позволяет констатировать, что для проверки истинности заключений в умозаключениях не обязательно обращаться всякий раз непосредственно к практике, а можно воспользоваться логическим (т. е. относящимся к форме рассуждения) критерием. Определяющим критерием истины служит практика. Логический же критерий истинности — вспомогательный и производный, вытекающий из практики и сам опирающийся на нее, как на окончательный критерий истинности.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 696; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.28.173 (0.008 с.) |



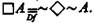
 («Earn необходимо, что А, то А»);
(«Earn необходимо, что А, то А»); («Если А, то возможно, что А»);
(«Если А, то возможно, что А»); («Необходимо, что А, тогда и только тогда, когда невозможно, что не-А»);
(«Необходимо, что А, тогда и только тогда, когда невозможно, что не-А»); («Возможно, что А, тогда и только тогда, когда не необходимо, что не-А»).
(«Возможно, что А, тогда и только тогда, когда не необходимо, что не-А»).
 — закон тождества.
— закон тождества.


