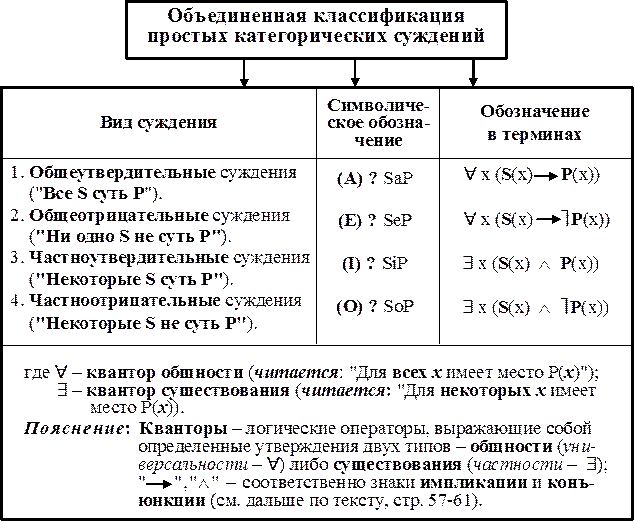Базовые понятия темы: «СУЖДЕНИЕ»

• Суждение — это форма мышления, в которой что-либо утверждается или отрицается о связи между предметом и его признаком либо об отношениях между предметами. Основной логической характеристикой суждения является его истинностное значение - каждое суждение либо истинно, либо ложно. Суждение истинно тогда, и только тогда, когда описываемая в нем ситуация имеет место в действительности, в противном случае оно ложно.

 

• Простым суждением называется суждение, выражающее связь двух терминов. Терминами в простом суждении называют субъект и предикат суждения. Субъектом суждения (S) называется то, о чем говорится в суждении, т.е. предмет мысли. Предикатом суждения (Р) называется то, что говорится о субъекте, какие признаки ему приписываются или не приписываются. Помимо субъекта и предиката в структуру суждения входят квантор и связка. Квантор суждения указывает на количество суждения, т.е. указывает на общее, частичное или единичное количество субъекта суждения (выражается словами «все», «ни один», «некоторые», «этот»). Связка обозначает отношение между субъектом (S) и предикатом (Р) суждения, благодаря чему мысль обретает форму суждения. Связка указывает на качество суждения. (Выражается словами «есть», «не есть», «является», «не является»).

 

• Объединенная классификация простых категорических суждений. В зависимости от количества и качества различают общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные суждения.

Общеутвердительным (А) называют суждение общее по количеству и утвердительное по качеству. Каноническая форма «Все S есть Р».

Общеотрицательным (Е) называют суждение общее по количеству и отрицательное по качеству. Каноническая форма «Ни одно S не есть Р».

Частноутвердительным ( I ) называют суждение частное по количеству и утвердительное по качеству. Каноническая форма «Некоторые S есть Р».

Частноотрицательным (О) называют суждение частное по количеству и отрицательное по качеству. Каноническая форма «Некоторые S не есть Р».

 

• Распределенность терминов в простых категорических суждениях. В простых суждениях термины могут быть распределены (S⁺, Р ⁺), либо не распределены (S^-, Р^-). Термин называется распределенным, если в суждении он взят в полном объеме. Термин называется нераспределенным, если в суждении он взят в части объема. Распределенность терминов в суждении выводится из определения отношений между понятиями, которыми выражаются термины суждения. При определении распределенности терминов в простых категорических суждениях следует руководствоваться следующими правилами:

а) В общеутвердительных суждениях (А): субъект (S) всегда распределен и предикат (Р) всегда нераспределен в случае отношения подчинения между субъектом и предикатом суждения; субъект (S) всегда распределен и предикат (Р) всегда распределен в случае отношения эквивалентности между субъектом и предикатом суждения;

b) В общеотрицательных суждениях (Е): субъект (S) и предикат (Р) суждения всегда распределены;

с) В частноутвердительных суждениях ( I ): субъект (S) и предикат (Р) нераспределены в случае отношения перекрещивания между субъектом и предикатом суждения; и субъект (S) нераспределен, а предикат (Р) распределен в случае отношения подчинения между предикатом и субъектом суждения;

d) В частноотрицательные суждениях (О): субъект суждения (S) всегда нераспределен, а предикат суждения (Р) всегда распределен.

 

• Сложным суждением называется суждение, состоящее из нескольких простых, связанных логическими связками. Запись сложного суждения на символическом языке логики, в котором простые суждения заменены на символы р, q, r, s, t …, а логические союзы на замещающие их символы Ù, v,, →, ↔ называется логической формой сложного суждения. Можно выделить пять основных видов логической связи:

- утверждение одновременного наличия нескольких ситуаций - конъюнкция (Ù);

- утверждение наличия хотя бы одной их нескольких ситуаций - слабая дизъюнкция (v);

- утверждение наличия только одной из нескольких ситуаций - сильная дизъюнкция ();

- одна ситуация является достаточным условием для возникновения другой ситуации - импликация (→);

- одна ситуация является достаточным и необходимым условием для возникновения другой ситуации - эквиваленция (↔).

В зависимости от вида логической связи различают следующие сложные суждения:

- соединительные суждения — суждения, в которых простые суждения соединены между собой логической связкой конъюнкция (Ù). Логическая форма: (р Ù q);

- разделительные суждения — суждения, в которых простые суждения соединены между собой логической связкой слабая дизъюнкция (v) или сильная дизъюнкция (). Логическая форма: (р v q); (рq);

- условные суждения - суждения, в которых простые суждения соединены между собой логической связкой импликация (→) или эквиваленция (↔). Логическая форма: (р → q), (р ↔ q), где р - основание суждения, q - следствие суждения. В условных суждениях в правильной логической форме основание всегда стоит вначале, а заключение в конце формулы.

Истинностные значения сложных суждений зависят от истинностных значений составляющих суждений и от типа их связи, что определяется посредством составления таблиц истинности:

- конъюнкция (Ù) принимает значение «Истина» только в случае одновременной истинности всех переменных; в остальных случаях конъюнкция принимает значение «Ложь» (См.: Рис. 18);

 

"и" p "и" q	"то" (p Ù q)
И	И	И
И	л	Л
Л	и	л
Л	л	л

 

Рис. 18.

 

- слабая (нестрогая) дизъюнкция (v) принимает значение «Ложь» только в случае одновременной ложности всех переменных; в остальных случаях слабая дизъюнкция принимает значение «Истина» (См.: Рис. 19);

 

p "или" ("и") q	"то" (pÚq)
И	И	И
И	л	И
Л	и	И
Л	л	л

 

Рис. 19.

 

- сильная (строгая) дизъюнкция () принимает значение «Ложь» в случае одновременной истинности или ложности всех переменных; в остальных случаях сильная дизъюнкция принимает значение «Истина» (См.: Рис. 20);

 

"или" p "или" q	"то" (p q)
И	И	Л
И	л	И
Л	и	И
Л	л	л

 

Рис. 20.

 

 

- импликация (→) принимает значение «Ложь» только в случае истинности основания суждения и ложности следствия суждения; в остальных случаях импликация принимает значение «Истина» (См.: Рис. 21);

 

"если" p "то" q	"то" (p → q)
И	И	И
И	л	Л
Л	и	И
Л	л	И

 

 

Рис. 21.

 

- эквиваленция (↔) принимает значение «Ложь» в случае истинности основания и ложности следствия суждения, либо наоборот, ложности основания и истинности следствия суждения; в остальных случаях эквиваленция принимает значение «Истина» (См.: Рис. 22).

"если и только если" p "то" q	"то" (p ↔ q)
И	И	И
И	л	Л
Л	и	Л
Л	л	И

 

 

Рис. 22.

• отрицание суждения — это операция, состоящая в преобразовании логического содержания отрицаемого суждения, конечным результатом которой является формулирование нового суждения, находящегося в отношении противоречия к исходному суждению. Отрицание простого атрибутивного суждения производится согласно следующим эквиваленциям: А = О; Е = I; I = Е; О = А — где А, Е, I, О — виды простых категорических суждений, - знак внешнего отрицания.

Отрицание сложного суждения производится согласно следующим эквиваленциям:

(р Ù q) ↔ (р v q) – 1-й закон де Моргана

(р v q) ↔ (р Ù q) – 2-й закон де Моргана

(р q) ↔ (р ↔ q)

(р → q) ↔ (р Ù q)

(р ↔ q) ↔ (р Ù q) v (р Ù q)

 

Выразим сказанное выше в виде комплексных схем:

Рис. 23-24

 

 

Рис. 25.

 

 

Рис. 26.

Примечание:

Происхождение символов " A", " I", " E" и " O" основано на следующем соглашении: " A" и " I" есть первые гласные буквы термина A ff i rmo (лат. "утверждаю"), а " E" и " O" – первые гласные буквы термина N e g o (лат. "отрицаю").

 

Рис. 27.

Типовые примеры по теме «Суждение»

Задание 6. Приведите высказывание к правильной логической форме, дайте объединенную классификацию суждений, приведите их схемы и принятые в логике обозначения А, Е, I, О.

 

Для решения задачи воспользуемся алгоритмом приведения предложений естественного языка к канонической форме категорических суждений и анализа простых суждений.

1. Определить субъект и предикат высказывания, обозначив их соответственно S и Р (составные S и Р подчеркнуть одной сплошной чертой).

2. При определении предиката следует иметь в виду следующее:

- если предикат выражен существительным или словосочетанием с существительным, то в данном случае предикат остается без изменения.

Образец 1:

«Некоторые юристы (S) - адвокаты (Р)».

 

- если предикат выражен прилагательным или причастием, которое может быть представлено одним словом или словосочетанием, то в этом случае к предикату следует добавить родовое понятие для субъекта высказывания.

Образец 2:

«Некоторые розы (S) красивы (Р)». → «Некоторые розы (S) — красивые цветы (Р)».

 

- если предикат выражен глаголом, который может быть представлен одним словом или словосочетанием, то в таком случае к предикату следует добавить родовое понятие для субъекта высказывания, а глагол превратить в соответствующее ему причастие.

 

Образец 3:

«Некоторые студенты нашей группы (S) сдали сегодня по логике (Р)». → «Некоторые студенты нашей группы (S) есть учащиеся, сдавшие сегодня зачет по логике (Р)».

3. Определить кванторное слово («все», «некоторые», «ни одно», «это»).

4. Определить логическую связку («есть», «не есть»)

5. Записать суждение в канонической форме: квантор - субъект (S) - связка - предикат (Р).

6. Записать формулу суждения, определить количественно-качественную характеристику суждения.

7. Графически изобразить отношения между терминами суждения.

8. Определить распределенность терминов.

 

Пример 1:

«Древние греки внесли большой вклад в развитие философии».

Решение:

1. В данном предложении логически определен только субъект — «древние греки» (S). Предикат выражен словосочетанием «внесли большой вклад в развитие философии» (Р).

2. Приводим предикат к канонической форме. Для этого подбираем к субъекту суждения («Древние греки») родовое понятие («Люди»). В канонической форме предикат будет выражен словосочетанием «Люди, внесшие большой вклад в развитие философии».

3. Кванторное слово в предложении отсутствует, но из анализа смысла предложения ясно, что речь идет только о некоторой части древних греков. Квантор суждения - «Некоторые».

4. В предложении утверждается наличие у субъекта «Древние греки» (S) свойства, выраженного в предикате «Внесли большой вклад в развитие философии» (Р). Значит логическая связка утвердительная («есть»).

5. Каноническая форма суждения: «Некоторые древние греки (S) есть люди. внесшие большой вклад в развитие философии (Р)».

6. Формула суждения — Некоторые S есть Р. Количественно-качественная характеристика суждения — частноутвердительное

7. Графически изображаем отношения между терминами суждения. Определяем отношение между понятием «Древние греки» (S) и понятием «Люди, несшие большой вклад в развитие философии» (Р) как отношение перекрещивания.

8. Определяем распределенность терминов: оба термина взяты в части объема, значит, они являются нераспределенными (S ^-, Р ^-) (Рис. 28).

 

Рис. 28.

Пример 2:

«Никто не может нести уголовную ответственность дважды за одно и то же преступление».

Решение:

1. В данном предложении субъект явно не определен. Из анализа смысла высказывания ясно, что речь идет о понятии «Человек» ( S ). Предикат выражен словосочетанием «Может нести уголовную ответственность дважды за одно и то же преступление» (Р).

2. Приводим предикат к канонической форме. Для этого подбираем к субъекту суждения («Человек») родовое понятие («Живое существо»). В канонической форме предикат будет выражен словосочетанием «Живое существо, которое может нести уголовную ответственность дважды за одно и то же преступление» (Р).

3. Кванторное слово в предложении отсутствует, но из анализа смысла предложения ясно, что речь идет обо всем объеме понятия «человек» (S). Квантор суждения — «Ни одно».

4. В предложении отрицается наличие у субъекта «Человек» (S) свойства, выраженного в предикате «Может нести уголовную ответственность дважды за одно и то же преступление» (Р). Логическая связка отрицательная («не есть»).

5. Записываем суждение в канонической форме: «Ни один человек (S) не есть живое существо, которое может нести уголовную ответственность дважды за одно и то же преступление (Р)».

6. Записываем формулу суждения - Ни одно S не есть Р. Определяем количественно-качественную характеристику суждения - общеотрицательное (Е).

7. Графически изображаем отношения между терминами суждения. Определяем отношение между понятием «Человек» (S) и понятием «Живое существо, которое может нести уголовную ответственность дважды за одно и то же преступление» (Р) как отношение несравнимости.

8. Определяем распределенность терминов: оба термина взяты в полном объеме, значит, они являются распределенными (S ⁺, Р ⁺) (Рис. 29).

 

 

Рис. 29.

Пример 3:

«Некоторые грибы не являются съедобными».

Решение:

1. В данном предложении логически определен только субъект - «Грибы» ( S ). Предикат выражен словом «Съедобными» (Р).

2. Приводим предикат к канонической форме. Для этого подбираем к субъекту суждения («Грибы») родовое понятие («Живые организмы»). В канонической форме предикат будет выраженсловосочетанием «Съедобные живые организмы» (Р).

3. Кванторное слово в предложении присутствует, речь идет о части объеме понятия «Грибы» (S). Кванторное слово суждения — «Некоторые».

4. В предложении отрицается наличие у субъекта «Грибы» (S) свойства, выраженного в предикате «Съедобные» (Р). Логическая связка отрицательная («не есть»).

5. Записываем суждение в канонической форме: «Некоторые грибы (S) не есть съедобные живые организмы (Р)».

6. Записываем формулу суждения - Некоторые S не есть Р. Определяем количественно-качественную характеристику суждения - частноотрицательное (О).

7. Графически изображаем отношения между терминами суждения. Определяем отношение отношения между понятием «Грибы» (S) и понятием «Съедобный живой организм» (Р) как отношение перекрещивания.

8. Определяем распределенность терминов: S взят в части объема, а Р взят в полном объеме, значит, распределенность их такова: S ^- , Р ⁺ (Рис. 30).

 

 

Рис. 30.

 

Задание 7. Рассмотрите сложные суждения, выразите их в символической записи. Укажите антецедент и консеквент в импликативных суждениях.

 

Пример 1:

«Работник имеет право на защиту своих трудовых прав, свобод и законных интересов всеми не запрещенными способами».

Решение:

1. Расчленим данное сложное суждение на простые и выразим их в правильной записи, принятой в русском языке, т.е. в соотношении подлежащего и сказуемого и обозначим эти простые суждения в форме, принятой в формальной логике:

а) «Работник имеет право на защиту своих трудовых прав всеми не запрещенными способами» - (р);

б) «Работник имеет право на защиту своих свобод всеми не запрещенными способами» - (q);

в) «Работник имеет право на защиту своих законных интересов всеми не запрещенными способами» - (r).

2. В данном случае имеет место утверждение одновременного наличия нескольких ситуаций - конъюнкция (Ù);

3. Формула данного сложного суждения выглядит так:

р Ù q Ù r

4. р, q, r – конъюнкты.

Пример 2:

«Человечество может погибнуть то ли от истощения земных ресурсов, то ли от экологической катастрофы, то ли в результате третьей мировой войны».

Решение:

1. Расчленим данное сложное суждение на простые и выразим их в правильной записи, принятой в русском языке, т.е. в соотношении подлежащего и сказуемого и обозначим эти простые суждения в форме, принятой в формальной логике:

а) «Человечество может погибнуть от истощения земных ресурсов» - (р);

б) «Человечество может погибнуть от экологической катастрофы» - (q);

в) «Человечество может погибнуть в результате третьей мировой войны» - (r).

2. В данном случае имеет место утверждение наличия хотя бы одной их нескольких ситуаций, но могут одновременно наличествовать и другие ситуации - слабая дизъюнкция (v);

3. Формула данного сложного суждения выглядит так:

р v q v r

4. р, q, r – дизъюнкты.

Пример 3:

«Гражданин вследствие физического недостатка, болезни или неграмотности не может собственноручно подписаться, то по его просьбе сделку может подписать другой гражданин».

Решение:

1. Расчленим данное сложное суждение на простые и выразим их в правильной записи, принятой в русском языке, т.е. в соотношении подлежащего и сказуемого и обозначим эти простые суждения в форме, принятой в формальной логике:

а) «Гражданин вследствие физического недостатка не может собственноручно подписаться» - (р);

б) «Гражданин вследствие болезни не может собственноручно подписаться» - (q);

в) «Гражданин вследствие неграмотности не может собственноручно подписаться» - (r);

г) «По просьбе этого гражданина сделку может подписать другой гражданин» - (s).

2. В данном случае имеет место утверждение наличия хотя бы одной их нескольких ситуаций, но могут одновременно наличествовать и другие ситуации - слабая дизъюнкция (v); одна из этих ситуаций или все они одновременно является достаточным условием для возникновения другой ситуации - импликация (→); таким образом, имеет место совместно слабая дизъюнкция и импликация;

3. Формула данного сложного суждения выглядит так:

(р v q v r) → s

4. р, q, r – дизъюнкты; (р v q v r) – антецедент; s – консеквент.

 

Пример 4:

«Брак расторгается, если судом будет установлено, что дальнейшая совместная жизнь супругов и сохранение семьи стали невозможными».

Решение:

1. Расчленим данное сложное суждение на простые и выразим их в правильной записи, принятой в русском языке, т.е. в соотношении подлежащего и сказуемого и обозначим эти простые суждения в форме, принятой в формальной логике:

а) «Судом установлено, что дальнейшая совместная жизнь супругов стала невозможной» - (р);

б) «Судом установлено, что сохранение семьи стало невозможным» - (q);

в) «Брак расторгается» - (r).

2. В данном случае имеет место утверждение одновременного наличия нескольких ситуаций - конъюнкция (Ù); обе эти ситуации являются достаточным условием для возникновения другой ситуации - импликация (→); таким образом, имеет место совместно конъюнкция и импликация;

3. Формула данного сложного суждения выглядит так:

(р Ù q) → r

4. р, q – конъюнкты; (р v q) – антецедент; r – консеквент.

 

Задание 8. Запишите логические формулы сложных суждений на языке логики высказываний и постройте для них истинностные таблицы.

 

Для решения задачи воспользуемся алгоритмом анализа сложных высказываний:

1. Определить и записать все простые суждения, из которых состоит предложение. Обозначить их символами.

2. Определить логическую связь между простыми суждениями.

3. Записать формулу сложного суждения. Если суждение условное, то необходимо определить основание и следствие.

4. Составить и заполнить таблицу истинности сложного суждения.

 

Пример 1.

«Оскорбление может быть нанесено случайно или намеренно»

Решение:

1. Определяем и записываем простые суждения:

а) «Оскорбление может быть нанесено случайно» — (р)

б) «Оскорбление может быть нанесено намеренно» – (q)

2. Союз «или» в высказывании утверждает наличие только одной из двух ситуаций. Логическая связь в данном суждении - сильная дизъюнкция ().

3. Формула сложного суждения: р q.

4. Строим таблицу истинности для суждения данной формы.

 

Для построения таблицы истинности необходимо знать количество столбцов при входе в таблицу (количество переменных) и количество строк в таблице (х = 2 ⁿ, где х - количество строк в таблице, n — количество переменных формуле). В данной таблице три столбца (р, q, р q) и четыре строки (2² = 4). В первом столбце записываем все варианты истинности для р (И и Л). Во втором столбце против каждого из значений первого столбца фиксирует значения сначала оба раза как И, а затем оба раза как Л. Под знаком логического союза сильная дизъюнкция () записываем конечный результат, ориентируясь на таблицу истинности, помещенную на стр. 3, рис. 20. Формула данного суждения является выполнимой, так как она принимает и значение И, и значение Л.

 

р	q	р q
И	И	Л
Л	И	И
И	Л	И
Л	Л	Л

 

Система построения таблиц истинности для любого количества пропозициональных может быть понята из следующих соображений:

В общем случае число всех возможных наборов значений n переменных равно 2ⁿ. Например, число допустимых интерпретаций для одной переменной равно 2¹ = 1; для двух переменных - 2² = 4; для трех переменных – 2³ = 8; длячетырех переменных равно 16, для пяти - 32 и т.д.

К примеру, пусть последовательность пропозициональных переменных р₁, р₂, …p_n состоит только из одной переменной (n = 1). Тогда существует только два набора значений: < и > и < л >:

 

	р1
	и
	л

 

Пусть последовательность пропозициональных переменных р₁, р₂, …p_n состоит из двух переменных (n = 2). В этом случае наборами указанных значений будут такие пары (всего их четыре):

 

< и, и >, < л, и >, < и, л >, < л, л >.

 

	р1	р2
	и	и
	л	и
	и	л
	л	л

 

Если же данная последовательность содержит три переменные, то наборами таких значений будут такие сочетания (восемь троек):

<и, и, и>, <л, и, и>, <и, л, и>, <л, л, и>,

<и, и, л>, <л, и, л>, <и, л, л>, <л, л, л>

	р1	р2	р3
	и	и	и
	л	и	и
	и	л	и
	л	л	и
	и	и	л
	л	и	л
	и	л	л
	л	л	л

 

 

В формальной логике применяются следующие пропозициональные связки:, ^, v,, →, ↔, где

- символ отрицания (дополнения);

^ - символ конъюнкции (объединения);

v – символ нестрогой дизъюнкции (разделения-объединения);

– символ строгой дизъюнкции (разделения-исключения);

→ - символ импликации (логического следования).

↔ - символ эквиваленции (логического тождества).

В случае отрицания (дополнения) высказывание (А) принимает значение «истина» только в том случае, если А ложно. И наоборот, если А истинно, то (А) - ложно.

 

А	А
и	л
л	и

Пример 2.

«Повернувшись спиной к наиболее интригующим событиям истории, невозможно понять логику этой истории».

Решение:

1. Определяем и записываем простые суждения:

а) «Человек повернулся спиной к наиболее интригующим событиям истории» - р (основание)

б) «Человек не может понять логику этой истории» — q (следствие)

2. Союз «если, … то …» означает, что ситуация, выраженная основанием («человек повернулся спиной к наиболее интригующим событиям истории») является достаточным условием для возникновения ситуации, выраженной следствием («человек не может понять логику этой истории»). Логическая связь в данном суждении — импликация (→)

3. Формула суждения: р → q

4. Строим таблицу истинности для суждения данной формы (см. стр. 4, рис. 21).

Под знаком логического союза импликация (→) записываем его истинностные значения. Формула данного суждения является выполнимой, так как она принимает и значение И, и значение Л.

 

р	q	р → q
И	И	И
Л	И	И
И	Л	И
Л	Л	И

 

Пример 3.

«Если студент учится на этом факультете, то он способный или очень прилежный».

Решение:

1. Определяем и записываем простые суждения:

а) «Студент учится на этом факультете» - р (основание)

б) «Этот студент способный» - q (следствие)

в) «Этот студент прилежный» - r (следствие)

2. Союз «если.., то..» означает, что ситуация, выраженная основанием («человек учится на этом факультете») является достаточным условием для возникновения ситуации, выраженной следствием («он способный или очень прилежный»). Логическая связь в суждении — импликация (→). В следствии между суждениями стоит союз «или», который означает утверждение наличия хотя бы одной из двух ситуаций. Логическая связь - слабая дизъюнкция (v).

3. Формула суждения: р → (q v r)

4. Строим таблицу истинности для суждения данной формы. Количество столбцов во входе в таблицу равно трем (переменных в формуле — 3), а количество строк в таблице - 8. Для того чтобы определить истинностные значения данной формулы необходимо определить порядок действий. Первым действием находим истинностное значение слабой дизъюнкции (v), а затем истинностное значение импликации (→).

Истинностные значения импликации (→) являются истинностными значениями данной формулы. Формула данного суждения является выполнимой, так как она принимает и значение И, и значение Л.

 

q	r	р	q v r	р → (q v r)
И	И	И	И	И
Л	И	И	И	И
И	Л	И	И	И
Л	Л	И	Л	л
И	И	л	И	И
Л	И	л	И	И
И	Л	л	И	И
Л	Л	л	л	л

 

Задание 9. Определите модальность суждения, запишите суждения с помощью модальных операторов:

 

Модальность (от лат. modus – мера, способ) есть явно или неявно выраженная в суждении характеристика суждения, дополни­тельная информация о логическом и фактическом статусе суждения, о регу­лятивных, оценочных, временных и других его характеристиках, о степени его обоснованности.

Первоначальную информацию в суждении выражают, как мы уже знаем, субъ­ект, предикат, кванторное слово и способ выражения этой информации – формула (S – P).

Что касается дополнительной информации, то она может быть самой различной. Так, например, логик середины XIII в. Вильгельм Шервуд насчитывал шесть видов модальных форм: истинно, ложно, возможно, невозможно, случайно и необходимо. В современном же логическом мышлении чаще других применяются модальности, выступающие под именами алетическая, деонтическая и эпистемическая.

Понятие "алетическая" (от греч. aletheia – истина) означает "истинная". Алетическая модальность в этом смысле есть отношение к основному требованию логики – выражать критерии истинных и ложных высказываний.

Алетическая модальность есть выраженная в суждениях и терминах необходимости-случайности либо возможности-невозможности информация об особенностях логической или фактической детерминированности сужде­ний.

Утверждение необходимости существования чего-либо, как соответствие действительности, обозначается символически как  p.

Аналогично, утверждение необходимости несуществования чего-либо, как отрицательное соответствие действительности, обозначается - ÿ ù p.

 

Пример:

«Наличие причинной связи между действиями, совершенными данным лицом, и наступившими общественно-опасными последствиями (p) – непременное условие привлечения его к уголовной ответственности (q)».

В терминах алетической модальности данное высказывание выглядит так:

ÿ (p ® q).

В противоположность "необходимости", "случайность" не связана с неизбежностью, а фиксирует лишь частные события в их произвольном возникновении и существовании.

Пример:

«Загрязнение окружающей среды (p) иногда способствует возникновению сердечно-сосудистых заболе­ваний (q)».

В терминах алетической модальности данное высказывание выглядит так:

ù ÿ (p ® q).

Что касается "возможности" чего-либо, то она всегда связана с со­вместимостью рассматриваемого явления с другими явлениями, состав­ляющими для данного явления среду его существования.

Пример:

«Загрязнение окружающей среды (p) может способствовать возникновению сердечно-сосудистых и легочных заболеваний (q)».

В терминах алетической модальности данное высказывание выглядит так:

à (p ® q).

В свою очередь, "невозможность" чего-либо всегда связана с не­совместимостью данного явления с другими, являющимися для него его средой.

Пример: <