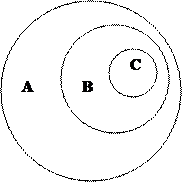Базовые понятия темы: «ПОНЯТИЕ»

• Понятие — форма мышления, в которой обобщены и выделены в класс предметы по общему только для них признаку (или по системе признаков). Логическую форму понятия в общем виде на языке логики предикатов можно представить как хР(х). Приведенное выражение читается: «Предмет х такой, что обладает признаком Р(х)».

 

• Содержание понятия, выраженного общей логической формой хР(х), - это признак (система признаков) Р(х), на основе которого (которых) осуществлено обобщение и выделение предметов в данном понятии. Содержание понятия выражается предикатом Р(х).

 

• Объем понятия, выраженного общей логической формой хР(х), - это класс всех элементов из универсума (U), обладающих признаком Р(х), т.е. множество всех предметов, которые характеризуются признаком (системой признаков), составляющих (составляющей) содержание понятия. Объем понятия, выраженного общей логической формой хР(х) обозначается WхР(х) — класс предметов х из универсума U, для которых истинно Р(х).

 

• Закон обратного отношения между объемом и содержанием понятия — с увеличением объема понятия уменьшается его содержание, и, наоборот, с увеличением содержания понятия уменьшается его объем.

 

• Отношение сравнимости по содержанию - понятия хР₁(х) и хР₂(х) сравнимы, если в содержании этих понятий имеется хотя бы один общий признак.

 

• Отношение несравнимости по содержанию - понятия хР₁(х) и хР₂(х) несравнимы, если в содержании этих понятий нет общего признака.

 

• Отношение совместимости между понятиями по объемам — понятия хР₁(х) и хР₂(х) совместимы, если они имеют общие элементы объема. Совместимые понятия могут находиться в отношениях эквивалентности, подчинения, перекрещивания.

 

ü Эквивалентность (равнообъемность) (Рис. 1)

Понятия находятся в отношении эквивалентности, если каждый элемент объема понятия хР₁(х) (А) является элементом объема понятия хР2 (х) (В), и наоборот, каждый элемент объема понятия хР₂(х) (В) является элементов объема понятия хР₁(х) (А).

ü Подчинение (включение) (Рис. 2)

Понятия находятся в отношении подчинения, если каждый элемент объема понятия хР₁(х) (А) является элементом объема понятия хР₂(х) (В), но не наоборот. При этом понятие хР₁(х) с объемом А называется видовым, а понятие хР₂(х) с объемом В – родовым.

 

ü Перекрещивание (пересечение) (Рис. 3)

Понятия находятся в отношении перекрещивания, если некоторые (но не все) элементы объема понятия хР₁(х) (А) являются элементами объема понятия хР₂(х) (В), и наоборот, некоторые (но не все) элементы объема понятия хР₂(х) (В) являются элементами объема понятия хР₁(х) (А).

• Отношение несовместимости между понятиями по объемам - понятия хР₁(х) (А) и хР₂(х) (В) несовместимы, если они не имеют общих элементов объема. Несовместимые понятия могут находиться в отношениях соподчинения, контрадикторности.

 

ü Соподчинение (Рис. 4)

Понятия находятся в отношении соподчинения, если ни один элемент объема понятия хР₁(х) (А) не является элементом объема понятия хР₂(х) (В), и наоборот, ни один элемент объема понятия хР₂(х) (В) не является элементом объема понятия хР₁(х) (А), и при этом объем понятия хР₁(х) (А) и объем понятия хР₂(х) (В) не исчерпывают объем родового понятия х ₃(х) (С).

 

ü Контрарность (противоположность) (Рис. 5)

Понятия находятся в отношении котрадикторности, если ни один элемент объема понятия хР₁(х) (А) не является элементом объема понятия хР₂(х) (В), и наоборот, ни один элемент объема понятия хР₂(х) (В) не является элементом объема понятия хР₁(х) (А), и при этом объем понятия хР₁(х) (А) и объем понятия хР₂(х) (В) в своей совокупности не полностью составляют объем родового понятия х ₃(х) (С).

 

ü Контрадикторность (противоречие) (Рис. 6)

Понятия находятся в отношении котрадикторности, если ни один элемент объема понятия хР₁(х) (А) не является элементом объема понятия хР₂(х) (В), и наоборот, ни один элемент объема понятия хР₂(х) (В) не является элементом объема понятия хР₁(х) (А), и при этом объем понятия хР₁(х) (А) и объем понятия хР₂(х) (В) полностью исчерпывают объем родового понятия х ₃(х) (С).

• Обобщение понятия — это логическая операция с понятием, состоящая в переходе от некоторого видового понятия хР₁(х) с меньшим объемом (А) к некоторому родовому понятию хР₂(х) с большим объемом (В). Пределом обобщения понятия являются категории, так как они не имеют родового понятия.

 

• Ограничение понятия — это логическая операция с понятием, состоящая в переходе от некоторого родового понятия хР₁(х) с большим объемом (А) к некоторому видовому понятию хР₂(х) с меньшим объемом (В), Пределом ограничения понятия являются единичные понятия, так как их объем содержит всего один элемент.

 

• Деление понятия - это логическая операция с понятием, посредством которой объем делимого понятия WхР(х) распределяется на подклассы (подмножества) WхР₁(х), WхР₂(х),..., WхР_n(х), являющиеся объемами видовых понятий по отношению к объему делимого (родового) понятия с точки зрения некоторого признака, называемого основанием деления.

 

ü Логическая структура деления

1. Делимое понятие, т.е. родовое понятие, объем которого раскрывается посредством деления (WхР(х)).

2. Члены деления, т.е. видовые понятия, которые получаются в;результате деления (WхР₁(х), WхР₂(х),..., WхР_n(х)).

3. Основание деления, т.е. признак, который образует виды предметов, обобщенных в делимом понятии. Если исходное понятие имеет вид хР(х), где Р(х) — родовой признак делимого понятия, то видовыми признаками членов деления будут Р(х) & Р₁(х), Р(х) & Р₂(х), Р(х) & Р₁(х).

ü Виды деления

• Деление по изменению видообразующего признака — деление объема понятия на подклассы (виды) по определенному признаку, называемому основанием деления.

• Дихотомическое деление — деление объема понятия на два подкласса (вида), обозначаемые двумя противоречащими друг другу понятиями.

 

ü Правила деления

1. Деление должно быть соразмерно. При делении по видообразующему признаку объединение членов деления должно совпадать с объемом делимого понятия.

2. Деление должно производиться только по одному основанию.

3. Члены деления должны исключать друг друга. Объемы членов деления не должны иметь общих элементов.

4. Деление должно быть последовательным. В процессе деления родового понятия следует переходить к ближайшим видовым понятиям, не пропуская их.

5. Операцию деления понятия нельзя подменять операцией расчленения целого на части. Операция деления предполагает отношение «род — вид» между делимым понятием и членами деления. Между целым и частью невозможно установить родовидовые отношения.

 

• Определение понятия - это логическая операция с понятием, заключающаяся в раскрытии содержания понятия или придания смысла некоторому термину.

 

ü Логическая структура определения:

• определяемое понятие, - то, что определяется;

• определяющее понятие — то, посредством чего определяется содержание определяемого понятия.

 

ü Виды определения

• Явные определения — определения, имеющие вид: Dfd = _df Dfn, где Dfd — определяемое понятие, = _df — равенство по определению, Dfn — определяющее понятие. К явным определениям относят родовидовые определения. Это такие определения, где определяющая часть начинается с указания родового понятия по отношению к определяемому понятию, а заканчивается указанием видового отличия определяемого понятия. В зависимости от характера видового отличия различают: атрибутивно-реляционные определения — в видовом отличии указываются качества и свойства определяемого понятия; генетические определения — в качестве видового отличия выступает способ происхождения, образования определяемого понятия; операциональные определения — в качестве видового отличия выступает способ отличения определяемого понятия от других понятий.

К явным определениям также относят: определения через перечисление — в определяющей части перечисляются те предметы,которые подпадают под определяемое понятие; определения через абстракцию - в определяющей части указывается то общее у предметов, что делает их равными друг другу в конкретной (определенной) ситуации.

- Неявные определения - определения, не имеющие формы равенства: Dfd = _df Dfn. В неявных определениях между определяемой и определяющей частью нет четких границ. К неявным определениям относят контекстуальные, индуктивные и аксиоматические определения. Контекстуальными называются такие определения, в которых содержание понятия определяется соответствующим фрагментом текста (контекстом), на основе анализа которого определение впоследствии может быть сформулировано в явной форме. Индуктивными называются определения, которые позволяют из исходных объектов путем применения к ним определенных операций получать новые объекты. Аксиоматическими называют определения, в которых содержание понятия задается системой аксиом, в состав которых входит определяемое понятие.

 

ü Правила определения

1. Определение должно быть соразмерным. Объем определяемого понятия должен быть равен объему определяющего понятия.

2. Определение не должно заключать в себе круга. Данное правило предполагает, что в определяющей части (Dfn) явного определения не должно встречаться определяемое понятие, а также понятия, встречающиеся в определяющей части (Dfn) любой системы определений не должны определяться через определяемое понятие (Dfd).

3. Определение должно быть ясным. Данное правило предполагает знание содержания и значения всех понятий, входящих в определяющую часть (Dfn), а также понимания смысла всей определяющей части (Dfn) в целом.

4. Определение нельзя подменять приемами, сходными с определением. К таким приемам относится: указание — разъяснение слов или словосочетаний путем непосредственного указывания на предметы, явления или процессы, обозначаемые этими словами или словосочетаниями; описание — перечисление некоторых внешних признаков предметов, по которым эти предметы можно обнаружить и отличить; характеристика — указание наиболее типичных черт - не обязательно наглядно воспринимаемых - предметов данного класса, сравнение — указание некоторых общих черт предметов данного класса по сравнению с другими предметами и, возможно, указании отличия первых от вторых.

Выразим сказанное выше в виде комплексных схем:

 

Рис. 7.

 

Рис. 8.

 

Рис. 9.

Рис. 10.

Типовые примеры по теме «Понятие»

Задание 1. Дайте полную логическую характеристику понятиям.

а)«Министр»; b) «Общественное порицание».

 

Исходя из схемы (Рис. 7), отметим, что понятия можно классифицировать по содержанию и по объему. Классификация понятий по содержанию - понятия конкретные или абстрактные, положительные или отрицательные, соотносительные и безотносительные. Классификация понятий по объему – понятия общие и единичные, регистрирующие или нерегистрирующие, разделительные или собирательные.

Отсюда понятия:

а)«Министр»:

Решение:

Понятие «Министр» по содержанию: конкретное (так как понятие отражает самостоятельный предмет); положительное (так как понятие отражает действительно существующие предметы); безотносительное (так как для данного понятия отсутствует понятие противоположного значения).

Понятие по объему: общее (так как данное понятие отражает класс предметов); регистрирующее (так как данное понятие отражает предметы, поддающиеся учету); разделительное (так как данное понятие отражает отдельно существующие предметы).

b) «Общественное порицание»

Решение:

Понятие «Общественное порицание» по содержанию: абстрактное (так как данное понятие выражает отношение между предметами (юридическими или физическими лицами); положительное (так как данное понятие не является отрицательным); соотносительное (этому понятию соответствует его противоположное понятие – «Общественное поощрение».

Понятие по объему: данное понятие является абстрактным, т.е. неотражающим предметы как таковые, а отражающим только лишь отношение между предметами (юридическими или физическими лицами), но абстрактные понятия по объему не классифицируются, так как объем понятия составляют именно сами предметы, которые отражает данное понятие.

Задание 2. Произведите последовательную многоступенчатую операцию обобщения и ограничения понятий.

а) «МГУ им. М.В. Ломоносова»

Решение:

Обозначим понятие «МГУ им. М.В.Ломоносова» как А ( Рис. 11 ).

Для того чтобы, произвести операцию обобщения, необходимо перейти от понятия А к понятию с большим объемом — понятию В. При этом содержание понятия В будет меньше чем у понятия А. Это можно сделать путем отбрасывания признака, включенного в содержание понятия А («им. М.В. Ломоносова»). Понятие В — понятие «Московский университет». Обобщением понятия В будет понятие С — «Университет» (получено путем отбрасывания признака «Московский»).

 

Рис. 11.

 

Таким образом, «цепочка» обобщения понятия выглядит так: «МГУ им. М.В.Ломоносова» → «Московский университет» → «Университет».

Операцию ограничения понятия А произвести невозможно, так как понятие «МГУ им. М.В. Ломоносова» - единичное понятие, а единичные понятия не могут ограничиваться.

 

b) «Отличник»

Решение:

Обозначим понятие «Отличник» как А ( Рис. 12 ).

Для того чтобы, произвести операцию обобщения, необходимо перейти от понятия А к понятию с большим объемом — понятию В. При этом содержание понятия В будет меньше, чем у понятия А. Это можно сделать путем отбрасывания признака, включенного в содержание понятия А («отлично успевающий»). Понятие В — понятие «Учащийся». Обобщением понятия В будет понятие С – «Человек» (получено путем отбрасывания признака «быть учащимся»).

 

 

Рис. 12.

 

Таким образом, «цепочка» обобщения понятия выглядит так: «Отличник» → «Учащийся» → «Человек».

 

Обозначим понятие «Отличник» как А ( Рис. 13 ).

Произведем операцию ограничения данного понятия. Для того чтобы, произвести операцию ограничения, необходимо перейти от понятия А к понятию с меньшим объемом — понятию В. При этом содержание понятия В будет больше, чем у понятия А. Это можно сделать путем прибавления признака, не включенного в содержание понятия А. Понятие В — понятие «Отличник 3 «Б» класса». Обобщением понятия В будет понятие С — «Отличник 3 «Б» класса школы №1».

Рис. 13.

Таким образом, «цепочка» ограничения понятия выглядит так: «Отличник» → «Отличник 3 «Б» класса» → «Отличник 3 «Б» класса школы №1».

Задание 3. Определить вид отношений между понятиями и выразить эти отношения с помощью круговых схем.

 

а) «Логика», «Наука»;

Решение:

Обозначим понятие «Логика» как А, а понятие «Наука» как В. Исходя из высказывания «Всякая логика является наукой, но не всякая наука является логикой» определяем отношения между этими понятиями как отношение подчинения понятия А («Логика») понятию В («Наука»). Изобразим эти отношения графически (Рис. 14).

 

Рис. 14.

b) «Дерево», «Крона дерева»;

Решение:

Обозначим понятие «Дерево» как А, а понятие «Крона дерева» как В. Исходя из высказывания «Всякая крона дерева является частью дерева» определяем отношения между этими понятиями как отношение целого А («Дерево») и части В («Крона дерева»). Это несравнимые понятия (понятие «Дерево» конкретное, а понятие «Крона дерева» абстрактное, следовательно, они не имеют общего родового признака. Изобразим эти отношения графически (Рис. 15).

.

 

Рис. 15.

 

с) «Подросток», «Хулиган», «Подростковая преступность», «Малолетний преступник»

Решение:

Обозначим понятие «Подросток» как А, понятие «Хулиган» как В, понятие «Подростковая преступность» как С, понятие «Малолетний преступник» как D. Схема отношений между этими понятиями будет выглядеть следующим образом, так как будут истинными следующие высказывания: «Только некоторые подростки (А) являются хулиганами (В), и только некоторые хулиганы (В) — подростки (А), все малолетние преступники ( D ) — подростки (А), но не наоборот, только некоторые малолетние преступники ( D ) - хулиганы (В), и только некоторые хулиганы (В) - малолетние преступники ( D ). Подростковая преступность (С) — социальное явление, и поэтому понятие С несовместимо с остальными понятиями». Значит, между понятиями А и В - отношение перекрещивания, между А и D — отношение подчинения, между В и D - отношение перекрещивания, понятие С несравнимо с А, В и D.

 

Рис. 16.

d) «Переводчик»; «Человек, знающий иностранный язык»; «Человек, знающий французский язык»; «Человек, имеющий высшее образование»

Решение:

Обозначим понятие «Переводчик» как А, понятие «Человек, знающий иностранный язык» как В, понятие «Человек, знающий французский язык» как С, понятие «Человек, имеющий высшее образование» как D. Схема отношений между этими понятиями будет выглядеть следующим образом, так как будут истинными следующие высказывания: «Все переводчики (А) являются людьми, знающими иностранный язык (В), но не наоборот. Все люди, знающие французский язык (С) являются людьми, знающими иностранный язык (В), но не наоборот. Все люди, имеющие высшее образование ( D ) являются людьми, знающими иностранный язык (В), но не наоборот, Только некоторые переводчики (А) есть люди, знающие французский язык (С), и наоборот. Только некоторые переводчики (А) есть люди, высшее образование ( D ), и наоборот. Некоторые люди, знающие французский язык (С) есть люди, имеющие высшее образование ( D ), и наоборот». Значит, между понятиями. А, С и D — отношение перекрещивания, между А и В, С и В, О и В - отношение подчинения.

 

 

Рис. 17.

Задание 4. Проверьте правильность деления понятий; в неправильном делении определитt, какие правила нарушены.

а) «Юридическая ответственность может быть уголовной, гражданской, административной и дисциплинарной».

Решение:

Данное выражение - операция деления, так как раскрывается объем понятия «Юридическая ответственность». Структура деления: «Юридическая ответственность» - делимое понятие; «уголовная, гражданская, административная и дисциплинарная ответственность» - члены деления; основание деления - характер правонарушений, связанных с типом правоотношений. Вид данного деления — деление по изменению видообразующего признака, так произошло деление объема понятия на подклассы (виды) по определенному признаку. Операция произведена правильно, так как в ней не нарушены правила деления.

 

b) «Год состоит из зимы, весны, лета и осени».

Решение:

В данном выражении не произведена операция деления, так как между понятием «год» и понятиями «зима», «весна», «лето», «осень» нет родовидовых отношений, т.е. предметы, мыслимые в этих понятиях — не элементы понятия «год», как это должно быть при делении понятия. В данном выражении произведена операция расчленения предмета на его части.

Задание 5. Установите правильность следующих определений (в неправильных определениях укажите, какие правила нарушены; дайте правильное определение:

а) «Шар представляет собой тело, образованное вращением полукруга вокруг диаметра».

Решение:

В данном выражении произведена операция определения, так как в нем раскрывается содержание понятия «Шар». Структура определения: «Шар» - определяемое понятие, «тело, образованное вращением полукруга вокруг диаметра» - определяющее понятие. Вид данного определения - явное, родо-видовое,так как определяющая часть начинается с указания рода определяемого понятия («Тело»), а заканчивается указанием видового отличия определяемого понятия («образованное вращением полукруга вокруг диаметра»). Определение генетическое, так как видовое отличие указывает способ создания предмета. Операция определение произведена правильно, так как в ней не нарушены правила определения.

 

b) «Попугай — птица тропических стран с ярким и пестрым оперением».

Решение:

В данном выражении произведена операция определения, так как в нем раскрывается содержание понятия «Попугай». Структура определения: «Попугай» - определяемое понятие, «птица тропических стран с ярким и пестрым оперением» - определяющее понятие. Вид данного определения — явное, родовидовое, так как определяющая часть начинается с указания рода определяемого понятия («птица тропических стран»), а заканчивается указанием видового отличия определяемого понятия («с ярким и пестрым оперением»). Определение атрибутивное, так как видовое отличие указывает дополнительно к родовому признаку отличительные признаки определяемого понятия. Определение неправильное, так как в нем нарушено правило определения. Объем определяющей части больше объема определяемого понятия, иначе говоря, определяющая часть не дает достаточной специфики попугаев.

 

с) «Скарлатина — заразная болезнь, преимущественно у детей, сопровождающаяся болью в горле, сыпью и последующим шелушением кожи».

Решение:

В данном выражении произведено описание предмета («Скарлатина»), в котором перечислены некоторые внешние признаки предмета («заразная болезнь, преимущественно у детей, сопровождающаяся болью в горле, сыпью и последующим шелушением кожи»), по которым этот предмет можно обнаружить и отличить.

 

Тема 2. Суждение