
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечнозначная логика как обобщение многозначной системы ПостаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исходя из системы Рщ Поста, мы (А. Г.) строим бесконечнозначную систему Gх0. Значениями истинности являются 1 (истина), 0 (ложь) и все дробные числа в интервале от 1 до 0,построенные в форме
Это числа: 1, ½, ¼, ¾, 1/8, 7/8, 1/16, 15/16, …,
Операции: отрицание, дизъюнкция, импликация и эквиваленция в Gх0 — определены следующими равенствами: 1. Отрицание: 2. Дизъюнкция: 3. Конъюнкция: 4. Импликация: 5. Эквиваленция: Отрицание в системе Gх0 является обобщением второго (симметричного) отрицания n -значной логики Поста. Посредством именно второго отрицания строятся конъюнкция, импликация и эквиваленция в системе G х0. Система Gх0 построенная предложенным способом, имеет множество тавтологий34. Тавтологией, например, является формула, гласящая, что отрицание р, повторенное два раза, даст первоначальное значение Тавтологии в Gх0 являются тавтологиями в двузначной логике, ибо бесконечнозначная система Gх0 является обобщением системы Ря Поста, а последняя есть обобщение двузначной логики. Для проверки правильности построения Gх0 предложенным нами способом на основании системы Gх0 построили систему G 3, взяв в качестве значений истинности 1, 1\2, 0. Система G 3 совпадает с системой Р 3Поста. Из системы G х0 также вычленяется 4-значная система G 4, значениями истинности аргументов которой являются 1, ½, ¼, 0, а значениями истинности функции: 1, ½, ¼, ¾, 0. Отрицание определяется по формуле
Конъюнкция, дизъюнкция, импликация, эквиваленция в G 4определены табл. 23. Таблица 23
В 4-значной системе G 4содержится классическая двузначная логика [при значениях истинности 1 («истина») и 0 («ложь»)], а также система Р 3Поста (при значениях истинности 1, 1/2, 0). Аналогично из Gх0 вычленяется система G5, а также G6,,G7 G 8и т. д.
Об интерпретации системы Gх0 В системе Gх0 между крайними значениями истинности — 1 («истина») и 0 («ложь») лежит бесконечное число значений истинности: 1/2 ,1/4, 3/4, 1/8, 7/8 и т. д. Процесс познания осуществляется таким образом, что мы идем от незнания к знанию, от неполного, неточного знания к более полному и более точному, от относительной истины к абсолютной. Абсолютная истина (в узком смысле) складывается из бесконечной суммы относительных истин. Если значению истинности, равному 1, придать семантический смысл абсолютной истины, а значению 0 — значение лжи (заблуждения, отсутствия знания), то промежуточные значения истинности отразят процесс достижения абсолютной истины как бесконечный процесс, складывающийся из познания относительных истин, значениями которых в системе Gх0 являются 1 / 2 , ¼, ¾, 1 / 8, 7 / 8... — и т. д. Чем ближе значение истинности переменных (выражающих суждения) к 1, тем большая степень приближения к абсолютной истине. Так осуществляется процесс познания от незнания к знанию, от явления к сущности, от сущности первого порядка к сущности второго порядка и т. д. Этот бесконечный процесс познания и отражает бесконечнозначная система G х0, построенная нами как обобщение двузначной классической логики, характеризующей процесс познания в рамках оперирования предельными значениями истинности суждений — истина и ложь. Такова семантическая интерпретация бесконечнозначной системы Gх0 раскрывающая ее роль в процессе познания истины.
ИНТУИЦИОНИСТСКАЯ ЛОГИКА
Интуиционистская логика построена в связи с развитием интуиционистской математики. Интуиционистская школа основана в 1907 г. голландским математиком и логиком Л. Брауэром (1881—1966)35, но некоторые ее идеи выдвигались и ранее. Интуиционизм — философское направление в математике и логике, отказывающееся от использования абстракции актуальной бесконечности, отвергающее логику как науку, предшествующую математике, и рассматривающее интуитивную ясность и убедительность («интуицию») как последнюю основу математики и логики. Интуиционисты свою интуиционистскую математику строят с помощью финитных (конечных) средств на основе системы натуральных чисел, которая считается известной из интуиции. Интуиционизм включает в себя две стороны — философскую и математическую. Математическое содержание интуиционизма изложено в ряде работ математиков. Ведущие представители отечественной школы конструктивной математики отмечают положительное значение некоторых математических идей интуиционистов. В целом конструктивная математика существевно отличается от интуиционистской. Советский математик-конструктивист А. А. Марков (1903—1979) пишет о том, что конструктивное направление имеет точки соприкосновения с так называемой интуиционистской математикой. Конструктивисты сходятся с интуиционистами в понимании дизъюнкции и в силу этого признают правильной данную Брауэром критику закона исключенного третьего. Вместе с тем конструктивисты считают неприемлемыми методологические основы интуиционизма. В этом высказывании ясно разделены две стороны интуиционизма — математическая и философская. Если первая сторона имеет рациональную часть (в этой связи предпочтительнее говорить об интуиционистской математике или интуиционистской логике, а не об интуиционизме), то вторая сторона интуиционизма (его методологические, идеалистические, философские основы) совершенно неприемлема. Брауэр считал, что чистая математика представляет собой свободное творение разума и не имеет никакого отношения к опытным фактам. У интуиционистов единственным источником математики оказывается интуиция, а критерием приемлемости математических понятий и выводов является «интуитивная ясность». Но интуиционист Гейтинг вынужден признаться в том, что понятие интуитивной ясности в математике само не является интуитивно ясным; можно даже построить нисходящую шкалу степеней очевидности. Основой происхождения математики в конечном итоге является не какая-то «интуитивная ясность» — продукт сознания человека, а отражение пространственных форм и количественных отношений действительного мира. Гейтинг, как и Брауэр, в гносеологии тоже субъективный идеалист. Он утверждает, что для математической мысли характерно, что она не выражает истину о внешнем мире, а связана исключительно с умственными построениями36. Еще в 1936 г. советский математик А. Н. Колмогоров подверг критике субъективно-идеалистические основы интуиционизма, заявив, что невозможно согласиться с интуиционистами, когда они говорят, что математические объекты являются продуктом конструктивной деятельности нашего духа, ибо математические объекты являются абстракциями реально существующих форм независимой от нашего духа действительности. Интуиционисты не признают человеческую практику и опыт источником формирования математических понятий, методов математических построений и методов доказательств. Особенности интуиционистской логики вытекают из характерных признаков интуиционистской математики. В современной классической математике часто прибегают к косвенным доказательствам. Но их почти невозможно ввести в интуиционистской математике и логике, так как там не признаются закон исключенного третьего и закон Закон исключенного третьего для бесконечных множеств в интуиционистской логике не проходит потому, что Эта знаменитая проблема Гольдбаха (X. Гольдбах — математик) была поставлена им в 1742 г. и не поддавалась решению около 200 лет. Гольдбах высказал предположение, что всякое целое число, большее или равное шести, может быть представлено в виде суммы трех простых чисел. Для нечетных чисел она была положительно решена только в 1937 г. советским математиком — академиком И. М. Виноградовым; все достаточно большие нечетные числа представимы в виде суммы трех простых чисел. Это одно из крупнейших достижений современной математики. Но закон непротиворечия представители как интуиционистской, так и конструктивной логик считают неограниченно применимым. Брауэр первый наметил контуры новой логики. Идеи Брауэра формализовал Гейтинг, в 1930 г. построивший интуиционистское исчисление предложений с использованием импликации, конъюнкции, дизъюнкции и отрицания на основе 11 аксиом и двух правил вывода — модуса поненс (modus ponens) и правила подстановки. Гейтинг утверждает, что, хотя основные различия между классической и интуиционистской логиками касаются свойств отрицания, эти логики не совсем совпадают и в формулах без отрицания. Гейтинг отличает математическое отрицание от фактического: первое выражается в форме конструктивного построения (выполнения) определенного действия, а второе говорит о невыполнении действия (а «невыполнение» чего-либо не является конструктивным действием). Интуиционистская логика имеет дело только с математическими суждениями и лишь с математическим отрицанием, которое определяется через понятие противоречия, а понятие противоречия интуиционисты считают первоначальным, выражающимся или приводящимся в форме 1 = 2, Фактическое отрицание не связано с понятием противоречия. Проблемами интуиционистской логики в нашей стране занимаются К. Н. Суханов, М. И. Панов, А. Л, Никифоров и др.
КОНСТРУКТИВНЫЕ ЛОГИКИ
Конструктивная логика, отличная от логики классической, своим рождением обязана конструктивной математике. Конструктивная математика может быть кратко охарактеризована как наука о конструктивных процессах и нашей способности их осуществлять. В результате конструктивного процесса возникает конструктивный объект, т. е. такой объект, который задается эффективным (точным и вполне понятным) способом построения (алгоритмом)37. Конструктивное направление (в математике и логике) ограничивает исследование конструктивными объектами и проводит его в рамках абстракции потенциальной осуществимости (реализуемости), т. е. игнорирует практическое ограничение наших возможностей построений в пространстве, времени, материале. Между идеями конструктивной логики советских исследователей и некоторыми идеями интуиционистской логики (например, в понимании дизъюнкции, в отказе от закона исключенного третьего) имеются точки соприкосновения. Однако конструктивная и интуиционистская логики имеют существенные отличия. 1. Различные объекты исследования. В основу конструктивной логики, которая является логикой конструктивной математики, положена абстракция потенциальной осуществимости, а в качестве объектов исследования допускаются лишь конструктивные объекты (слова в определенном алфавите). В основу интуиционистской логики, являющейся логикой интуиционистской математики, положена идея «свободно становящейся последовательности» (т. е. последовательности, строящейся не по алгоритму), которую интуиционисты считают интуитивно ясной. 2. Обоснование интуиционистской математики и логики дается с помощью идеалистически истолкованной интуиции, а обоснование конструктивной математики и логики дается на базе научного математического понятия алгоритма (например, нормального алгоритма А. А. Маркова) или эквивалентного ему понятия рекурсивной функции. 3. Различные методологические основы. Методологической основой конструктивного направления в математике отечественные исследователи считают положения материализма, с позиций которого критерием истинности познания (в том числе и научного) является практика. Это положение сохраняет свою силу и для таких наук, как логика и математика, хотя здесь практика входит в процесс познания лишь опосредованно, в конечном счете. Интуиционисты же, оставаясь в рамках субъективно-идеалистической философии, считают источником формирования математических понятий и методов не человеческую практику, а первоначальную «интуицию», а критерием истинности в математике — «интуитивную ясность». 4. Различные интерпретации**. А. Н. Колмогоров рассматривал интуиционистскую логику как исчисление задач. А. А. Марков определял логические связки конструктивной логики как прилагаемые к потенциально осуществляемым конструктивным процессам (действиям). Интуиционистская логика Л. Брауэра и А. Гейтинга интерпретируется ими как исчисление предложений (высказываний), причем область высказываний у них ограничивается математическими предложениями. 5. Отличие ряда логических средств. Отечественные представители узко-конструктивной логики признают в качестве принципа: если имеется алгоритмический процесс и удалось опровергнуть, что он продолжается бесконечно, то, следовательно, процесс закончится. Некоторые из представителей конструктивной логики доказывают его в уточненной форме. Представители интуиционистской логики не признают этот принцип.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 747; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.195.30 (0.008 с.) |

 и в форме
и в форме  где к — целочисленный показатель.
где к — целочисленный показатель.
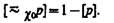




 Тавтологиями в Gх0 будут четыре правила де Моргана.
Тавтологиями в Gх0 будут четыре правила де Моргана.

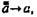 которые участвуют в косвенных доказательствах.
которые участвуют в косвенных доказательствах.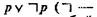 знак отрицания) требует общего метода для решения любой проблемы или, более явно, общего метода, который по произвольному высказыванию р позволил бы получать либо доказательство р, либо доказательство отрицания р. Гейтинг считает, что так как интуиционисты не располагают таким методом, то они и не вправе утверждать принцип исключенного третьего. Покажем это на таком примере. Возьмем утверждение: «Всякое целое число, большее единицы, либо простое, либо сумма двух простых, либо сумма трех простых». Неизвестно, так это или нет, хотя в рассмотренных случаях, которых конечное число, это так. Существует ли число, которое не удовлетворяет этому требованию? Мы не можем указать такое число и не можем вывести противоречие из допущения его существования.»
знак отрицания) требует общего метода для решения любой проблемы или, более явно, общего метода, который по произвольному высказыванию р позволил бы получать либо доказательство р, либо доказательство отрицания р. Гейтинг считает, что так как интуиционисты не располагают таким методом, то они и не вправе утверждать принцип исключенного третьего. Покажем это на таком примере. Возьмем утверждение: «Всякое целое число, большее единицы, либо простое, либо сумма двух простых, либо сумма трех простых». Неизвестно, так это или нет, хотя в рассмотренных случаях, которых конечное число, это так. Существует ли число, которое не удовлетворяет этому требованию? Мы не можем указать такое число и не можем вывести противоречие из допущения его существования.»


