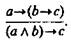Сокращенные условные, разделительные и условно-разделительные умозаключения

Категорический силлогизм в мышлении часто употребляется в сокращенной форме — в форме энтимемы. Сокращенными мо­гут быть не только простые категорические силлогизмы, но и условные, и разделительные, и условно-разделительные умоза­ключения, в которых может быть пропущена либо одна из посы­лок, либо заключение. Рассмотрим типы таких сокращенных умозаключений.

1. В умозаключении заключение в явном виде может не формулироваться. «Если данное тело — металл, то оно при на­ревании расширяется. Данное тело — металл». Заключение Данное тело при нагревании расширяется» не формулируетсяв явном виде, а просто подразумевается в этом условно-катего­рическом умозаключении.

В приводимом ниже разделительно-категорическом умозак­лючении также пропущено заключение. «Многоугольники делят­ся на правильные и неправильные. Данный многоугольник непра­вильный». Заключение «Данный многоугольник не является пра­вильным» опущено; оно легко может быть восстановлено.

В дилеммах и трилеммах заключение также может явно не формулироваться, а подразумеваться. Например, в приведенной ниже сложной деструктивной дилемме заключение явно не при­сутствует:

«Если соблюдать правила хранения зерна, то не произойдет его самозагорания, а если организовать хорошую охрану зернохранилища, то не произойдет умышленного поджога. Данный пожар произошел либо от самозагорания зерна, либо от умыш­ленного поджога». Заключение — «В данном зернохранилище либо не соблюдаются правила хранения зерна, либо не налажена охрана» — подразумевается, а не высказывается в явной форме.

2. В умозаключении пропущена одна из посылок. В умозак­лючениях может быть пропущена первая посылка; она может подразумеваться, если выражает известное положение, теорему, закон и т. д.

В условно-категорическом умозаключении «Сумма цифр дан­ного числа делится на 3, следовательно, данное число делится на 3» опущена первая посылка, формулирующая известную матема­тическую закономерность: «Если сумма цифр данного числа делится на 3, то все число делится на 3».

В приводимом ниже разделительно-категорическом умозак­лючении также пропущена первая посылка: «Существительное в русском языке может быть женского, мужского или среднего рода», а все умозаключение сокращенно формулируется так: «Данное существительное русского языка не является сущест­вительным ни женского рода, ни среднего рода. Следовательно, данное существительное мужского рода».

В приведенном ниже примере сложной конструктивной дилем­мы: «Если я пойду через болото, то могу попасть в трясину, а если я пойду в обход, то не успею вовремя доставить донесение. Следовательно, я могу попасть в трясину или не успею вовремя доставить донесение» — вторая посылка не формулируется, а лишь подразумевается: «Я могу идти через болото или в обход».

Можно было бы привести и другие примеры сокращенных умозаключений: чисто условных, условно-категорических, чисто разделительных, разделительно-категорических, условно-разде­лительных (дилемм, трилемм) с пропущенной первой или второй посылкой, — но предоставляем это самостоятельно сделать чи­тателю.

Итак, рассмотренные нами прямые выводы, такие, как чисто условные, чисто разделительные, условно-категорические, разде­лительно-категорические и условно-разделительные (лемматические) умозаключения, сформулированные полностью и сокра­щенные (т. е. в которых пропущена либо одна из посылок, либо заключение), широко используются в процессе научного и обы­денного мышления, в процессе обучения в школе и в вузе. Поэто­му знание правил построения этих видов умозаключений пре­достережет от логических ошибок в мышлении, поможет до­казательнее, аргументированнее строить свои рассуждения и сде­лать более эффективным обучение учащихся и студентов.

Прямые выводы кроме рассмотренных выше форм включают и такие виды:

1. Простая контрапозиция.

Правило простой контрапозиции имеет следующий вид:

Это правило читается так: «Если а имплицирует b, то отрица­ние b имплицирует отрицание а». Здесь а и b — переменные, обозначающие произвольные высказывания, или пропозицио­нальные переменные.

Пример:

1. Если данный треугольник равносторонний, то он равноугольный.

____________________________________________________________________

Если данный треугольник не равноугольный, то он не равносторонний.

 

2. Если это вещество фосфор, то оно непосредственно с водородом не сое­диняется.

_____________________________________________________________________________________

Если вещество непосредственно с водородом соединяется, то это вещество не является фосфором.

 

Заметим, что в логике высказываний

Формула называется законом простой контрапозиции.

2. Сложная контрапозиция.

— правило сложной контрапозиции.

Пример рассуждения по правилу сложной контрапозиции:

 

Если у меня будут деньги и я буду здорова, то я поеду домой на каникулы.

________________________________________________________________________

Если у меня были деньги и я не поехала на каникулы домой, то, следовательно, а не была здорова.

 

3. Правило импортации (конъюнктивного объединения условий). П. С. Новиков называет его правилом соединения посылок:

Это правило читается так: «Если а имплицирует, что b имп­лицирует с, то а и b имплицируют с».

В. А. Сухомлинский писал: «Если учитель стал другом ребен­ка, если эта дружба озарена благородным увлечением, порывом к чему-то светлому, разумному, в сердце ребенка никогда не появится зло». На основании правила соединения посылок (пра­вила конъюнктивного объединения условий) мы можем это вы­сказывание В. А. Сухомлинского записать иначе, но оно будет эквивалентно прежнему его высказыванию. Заключение: «Если учитель стал другом ребенка и эта дружба озарена благородным увлечением, порывом к чему-то светлому, разумному, то в сердце ребенка никогда не появится зло».

4. Правило экспортации (разъединения условий):

Это правило читается так: «Если а и b имплицируют с, то а имплицирует, что b имплицирует с. Правило это обратно предыдущему. Поэтому в качестве иллюстрации можно взять те же мысли В. А. Сухомлинского, только сначала прочитать наше полученное заключение, из которого можно прийти к высказыва­нию самого В. А. Сухомлинского.

 

НЕПРЯМЫЕ (КОСВЕННЫЕ) ВЫВОДЫ

 

К ним относятся: рассуждение по правилу введения имплика­ции; сведение «к абсурду»; рассуждение «от противного» (проти­воречащего).

1. Рассуждение по правилу введения импликации.

Правило вывода сформулировано так:

Данное правило читается так: «Если из посылок гамма (Г) и посылки а выводится заключение b, то из одних посылок Г выводится, что а имплицирует b». Это правило вывода имеет и другое название: «Теорема о дедукции». Здесь «Г» может быть и пустым множеством посылок.

Приведем пример рассуждения студента, поясняющий приве­денное правило. Пусть Г содержит следующие посылки: 1) «Я сдал экзамен по педагогике на «отлично»; 2) «Я сдал экзамен по логике на «отлично»; 3) «Я сдал экзамен по математике на отлично». Посылка а означает: «Я успешно выполнил всю порученную мне работу на факультете». Заключение b означает: «Я получу повышенную стипендию». То, что записано над чертой, будет содержательно прочитано так: «Если я сдал экзамены по педагогике, логике и математике на «отлично» и успешно выполнил всю порученную мне работу на факультете, то из этого последует заключение: «Я получу повышенную стипендию». То, что записано под чертой, содержательно можно прочитать так: Я сдал экзамены по педагогике, логике и математике на «отлич­но». Отсюда следует заключение: «Если я успешно выполню всю порученную мне работу на факультете, то я получу повышенную стипендию».

2. Правило сведения к абсурду. Это правило иначе называется правилом введения отрицания.

Правило читается так: «Если из посылок Г и посылки а выво­дится противоречие, т. е. b и не-b, то из одних Г выводится не-а». Метод сведения к абсурду широко применяется в мышлении, как научном, так и в полемическом и в обыденном.

В классической двузначной логике метод сведения к абсурду выражается в виде формулы:— противоречие или ложь.

Эта формула говорит о том, что суждение а надо отрицать (считать ложным), если из а вытекает противоречие.

Определение отрицания посредством сведения к абсурду, про­тиворечию широко используется не только в классической, но ив неклассических логиках: в многозначных, конструктивных и интуиционистской.

3. Правило непрямого вывода — рассуждение «от противно­го» (противоречащего). Доказательство «от противного» приме­няется тогда, когда нет аргументов для прямого доказательства. Методом «от противного» нередко доказываются математичес­кие теоремы.

Суть рассуждения «от противного» подробно будет показана в теме «Доказательство», в разделе «Косвенное доказательство».

Итак, мы рассмотрели правила прямых и непрямых (косвен­ных) выводов и убедились, что они широко применяются в мыш­лении. При этом было показано, как та или иная форма прямого или косвенного вывода наполняется конкретным содержанием, взятым из областей педагогики, математики, физики, этики и других областей науки и обыденного мышления, а также из опыта преподавания в средней школе.