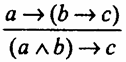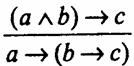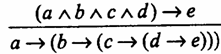Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В умозаключении пропущена одна из посылокСодержание книги
Поиск на нашем сайте
В умозаключениях может быть пропущена первая посылка, она может подразумеваться, если выражает какое-то истинное суждение, формулирующее известное положение, теорему, закон и т. д. В условно-категорическом умозаключении “Сумма цифр данного числа делится на 3, следовательно, данное число делится на З” опущена первая посылка, формулирующая известную математическую закономерность: “Если сумма цифр данного числа делится на 3, то все число делится на З”. В разделительно-категорическом умозаключении “Данное существительное русского языка не является существительным ни женского рода, ни среднего рода. Следовательно, данное существительное мужского рода” также пропущена первая посылка: “Существительное в русском языке может быть женского, или мужского, или среднего рода”. В сложной конструктивной дилемме “Если я пойду через болото, то могу попасть в трясину, а если я пойду в обход, то не успею вовремя доставить донесение. Следовательно, я могу попасть в трясину или не успею вовремя доставить донесение” не формулируется, а лишь подразумевается вторая посылка: “Я могу идти через болото или в обход”. Можно было бы привести и другие примеры сокращенных умозаключений: чисто условных, условно-категорических, чисто разделительных, разделительно-категорических, условно-разделительных (дилемм, трилемм) с пропущенной или первой, или второй посылкой, однако предоставим это сделать самому читателю. Итак, рассмотренные нами прямые выводы - такие, как чисто условные, чисто разделительные, условно-категорические, разделительно-категорические и условно-разделительные (лемматические) умозаключения, сформулированные как полностью, так и сокращенно (т. е. в которых пропущена либо одна из посылок, либо заключение), - широко используются в процессах научного и обыденного мышления, обучения в школе или в вузе. Знание правил построения этих видов умозаключений предостерегает от логических ошибок в мышлении, помогает доказательнее, аргументированное строить рассуждения и эффективнее применять приемы обучения учащихся и студентов. Прямые выводы (кроме рассмотренных выше форм) включают и такие виды (делаемые из одной посылки): Простая контрапозиция.
Это правило читается так: “Если а имплицирует, то отрицание b имплицирует отрицание а”. Здесь а и b – переменные, обозначающие произвольные высказывания, или пропозициональные переменные. Примеры: 1. Если данный треугольник равносторонний, то он равноугольный. Если данный треугольник не равноугольный, то он не равносторонний. 2) Если это вещество фосфор, то оно непосредственно с водородом не соединяется. Если вещество непосредственно с водородом соединяется, то это вещество не является фосфором. Заметим, что в логике высказываний (а→ b) Сложная контрапозиция.
((a ^ b) → с) Пример рассуждения по правилу сложной контрапозиции: Если у меня будут деньги и я буду здорова, то я на каникулы поеду домой. Если у меня были деньги и я на каникулы не поехала домой, то, следовательно, я не была здорова. 3. Правило импортации (конъюнктивного объединения условий).
Это правило читается так: “Если а имплицирует, что b имплицирует с, то а и b имплицируют с”. В. А. Сухомлинский писал: “Если учитель стал другом ребенка, если эта дружба озарена благородным увлечением, порывом к чему-то светлому, разумному, в сердце ребенка никогда не появится зло”. На основании правила соединения посылок (правила коньюктивного объединения условий) мы можем это высказывание В. А. Сухомлинского записать иначе, но оно будет эквивалентно прежнему его высказыванию: “Если учитель стал другом ребенка и эта дружба озарена благородным увлечением, порывом к чему-то светлому, разумному, то в сердце ребенка никогда не появится зло”.
Это правило читается так: “Если а и b имплицируют с, то а имплицирует, что b имплицирует с”. Это правило обратно предыдущему. Поэтому в качестве иллюстрации можно взять те же мысли В.А. Сухомлинского, только сначала прочитать нашу запись полученного заключения, откуда можно прийти к высказыванию самого В. А. Сухомлинского. Приведем другой, более сложный пример, иллюстрирующий правило экспортации (разъединения условий), в котором сформулированы не два, а четыре условия: “Если вы любите детей, полны жажды познания, имеете доброе сердце, мечтаете посвятить себя интересному творческому труду, то смело выбирайте профессию учителя”. Формула этого сложного суждения такая: (a^b^c^d)→е.
Сформулируем предыдущее суждение по-другому, но эквивалентным образом: “Если вы любите детей, если полны жажды познания, если имеете доброе сердце, если мечтаете посвятить себя интересному творческому труду, то смело выбирайте профессию учителя”.
Непрямые (косвенные) выводы К ним относятся: рассуждение по правилу введения импликации; сведение “к абсурду”; рассуждение “от противного” (противоречащего).
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.243 (0.006 с.) |

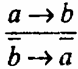
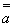
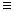 а. Формула:
а. Формула: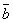
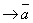 ) называется законом простой контрапозиции.
) называется законом простой контрапозиции.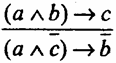 - правило сложной контрапозиции.
- правило сложной контрапозиции.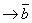 ) - это формула закона сложной контрапозиции.
) - это формула закона сложной контрапозиции.