
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Трехзначная система ГейтингаСодержание книги
Поиск на нашем сайте
В двузначной логике из закона исключенного третьего выводятся: 1 ) Импликация Гейтинга
Отрицание Гейтинга
Конъюнкция и дизъюнкция определяются обычным способом как минимум и максимум значении аргументов. Если учитывать лишь значения функций 1 и 0, то из матриц системы Гейтинга вычленяются матрицы двузначной логики.
этой трехзначной логике закон непротиворечия является тавтологией, но ни закон исключенного третьего, ни его отрицание тавтологиями не являются. Оба правильных модуса условно-категорического силлогизма, формула (х → у) → ( Хотя по сравнению с логикой Лукасевича в матрицах отрицания и импликации Рейтингом в его системе были произведены небольшие изменения, результаты оказались значительными: в системе Рейтинга являются тавтологиями многие формулы классического двузначного исчисления высказываний. т -значиая система Поста (Рт) 1 Система американского математика и логика Э. Л. Поста (1897- 1954) является обобщением двузначной логики, ибо при т = 2 в качестве частного случая мы получаем двузначную логику. Значения истинности суть 1, 2,..., т (при т Пост вводит два вида отрицания (N1x и N2х) соответственно называемые циклическим и симметричным. Они определяются путем матриц и посредством равенств. Первое отрицание определяется двумя равенствами: 1. [ N1x ]=[ x ]+1 при [ х ] 2. [ N1m ]=1. Второе отрицание определяется одним равенством: [ N 2 x ]= m -[ x ]+1 Характерной особенностью двух отрицаний Поста является то, что при т = 2 эти отрицания совпадают между собой и с отрицанием двузначной логики, что подтверждает тезис: многозначная система Поста есть обобщение двузначной логики. Этапы развития логики как науки и основные направления современной символической логики
Конъюнкция и дизъюнкция определяются соответственно как максимум и минимум значений аргументов. При указанных определениях отрицания, конъюнкции и дизъюнкции обнаруживается, что при значении для х, большем двух, законы непротиворечия и исключенного третьего, а также отрицание этих законов не являются тавтологиями. Трехзначная система Р3 Поста имеет следующую указанную в таблицах форму. В этих таблицах приняты обозначения, введенные Постом при m = 3: первое отрицание обозначается через (~ 3 р), второе отрицание - через ( рv3 р), импликация - через (р
Если в качестве значений истинности взяты лишь 1 “истина” и 3 “ложь”, то из таблиц системы Р3 Поста вычленяются таблицы для отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции двузначной логики. В системе Р3 тавтология принимает значение 1; закон исключенного третьего не является тавтологией ни для первого, ни для второго отрицания Поста, но является тавтологией закон исключенного четвертого для первого отрицания. Две бесконечнозначные системы Гетмановой: “Логика истины” и “Логика лжи” Бесконечнозначная “Логика истины” как обобщение многозначной системы Поста Исходя из т -значной системы Э. Л. Поста автор этого учебника А. Д. Гетманова построила бесконечнозначную систему Gxo. J В ней значениями истинности являются: 1 (“истина”), 0 (“ложь”) и все дробные числа в интервале от 1 до 0, построенные в форме (1/2)k и в форме (1/2)k*(2k - 1), где k -целочисленный показатель. Иными словами, значениями истинности являются: 1, 1/2, 1/4, 3/4, 1/8, 7/8, 1/16, 15/16,….., (1/2)k, (1/2)k*(2k-1),….,0. Операции: отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция в Gxo - определены следующими равенствами: 1. Отрицание: [ 2. Дизъюнкция: [ р v х0 q ] = max([ p ], [ q ]). 3. Конъюнкция: [ р 4. Импликация: [ р = х0х0 q ] = [ 5. Эквиваленция: [ р Отрицание в системе G xo является обобщением второго (симметричного) отрицания т -значной логики Поста. Посредством именно этого отрицания строятся конъюнкция, импликация и эквиваленция в системе Gхо. Система Gхо, построенная предложенным способом, имеет множество тавтологий. (Тавтология принимает значение 1). Тавтологии в бесконечнозначной “Логике истины” (т. е. в Gхо) являются тавтологиями в двузначной логике, ибо Gхо является обобщением системы Р Поста, а последняя есть обобщение двузначной логики. Из системы Gхо вычленяются G3,G4.,G5,G6,...,Gn,т.е. любая конечнозначная “Логика истины”. Об интерпретации системы Gхо В системе Gхо между крайними значениями истинности: 1 (“истина”) и 0 (“ложь”) лежит бесконечное число значений истинности: 1/2, 1/4, 3/4,1/8, 7/8 и т. д. Процесс познания осуществляется таким образом, что мы идем от незнания к знанию, от неполного, неточного знания к более полному и точному, от относительной истины к абсолютной. Абсолютная истина (в узком смысле) складывается из бесконечной суммы относительных истин. Если значению истинности, равному 1, придать семантический смысл абсолютной истины, а значению 0 - значение лжи (заблуждения, отсутствия знания), то промежуточные значения истинности отразят процесс достижения абсолютной истины как бесконечный процесс, складывающийся из познания относительных истин, значениями которых в системе Gхо являются 1/2, 1 / 4, 3/4,1/8, 7/8 и т. д. Чем ближе значение истинности переменных (выражающих суждения) к 1, тем большая степень приближения к абсолютной истине. Так осуществляется процесс познания: от незнания к знанию, от явления к сущности, от сущности первого порядка к сущности второго порядка и т. д. Этот бесконечный процесс познания и отражает бесконечнозначная система Gхо, построенная автором как обобщение двузначной классической логики, характеризующей процесс познания в рамках оперирования лишь предельными значениями истинности - “истина” и “ложь”. Такова семантическая интерпретация системы Gхо (“Логика истины”), вскрывающая ее роль в процессе познания истины Методологические проблемы применения многозначных логик для моделирования систем с наличием элемента неопределенности. (О применении многозначных логик в социологии). Многозначные логики используются при моделировании систем с наличием элемента неопределенности. Простейшим примером применения трехзначной логики является голосование: “за”, “против”, “воздержался” или ответы на вопросы: “да”, “нет”, “затрудняюсь ответить”. Более сложной методологической проблемой является применение многозначных логик при построении социологических анкет. Обычно дается ряд ответов на один вопрос. Ответы формулируются приблизительно так: “да”, “нет”, “скорее да, чем нет”, “скорее нет, чем да”, “удовлетворен в значительной степени”, “мало удовлетворен” и т. д. Все эти ответы включают значительный элемент неопределенности, что затрудняет выявление мнения людей в ходе социологического опроса (или анкетирования). Автор считает возможным использовать многозначные логики с различными значениями истинности, т. е., например, 6-ти, или 8-ми, или 9-ти, или 12-значные логики. Составляющий анкету социолог должен предлагать конкретные значения истинности суждений, т. е. предусмотреть точные оценки, которые даст сам человек, работающий с анкетой. Например, в 9-значнои логике значениями истинности будут следующие: 1,15/16,7/8,3/4,1/2,1/4,1/8, 1/16, 0. Если человек, например, при ответе на вопрос: “Удовлетворен ли он своим трудом?” им полностью удовлетворен, то в соответствующем разделе он напишет 1, если же он полностью не удовлетворен, то напишет значение 0. Если он почти удовлетворен (согласен), то напишет либо 15/16 либо 7/8; если же он почти не удовлетворен, то напишет 1/16 или 1/8. Если он не знает ответа или думает неопределенно, то напишет 1/2. При обработке информации на ЭВМ на основе данных числовых характеристик ответов можно получить более точные знания о мнении в репрезентативной выборке любого вида (стихийной, квотной, вероятностной и других, когда применяется неполная индукция) или во всей генеральной совокупности (т. е. при сплошном обследовании, когда применяется полная индукция). Бесконечнозначная система Fхо - “Логика лжи” Аристотель охарактеризовал ложь так: ложное говорит тот, “кто думает обратно тому, как дело обстоит с вещами”'. Ложь может быть не только измышлением о том, чего не было, но и сокрытием или отрицанием того, что было. Ложь бывает непреднамеренной (паралогизм) или преднамеренной (софизм). В мышлении ложь формулируется в виде суждений. Иногда понятие “ложь” употребляется как синоним понятия “заблуждение”. Ведь и ложь, и заблуждение - формы неистинного знания. Причины возникновения заблуждений сходны с теми, которые порождают ложь: ограниченность общественно-исторической практики, абсолютизация отдельных моментов процесса познания, нарушение логических правил доказательств, человеческие эмоции, догматический стиль мышления и др. Однако в отличие от лжи заблуждение выступает как неотъемлемый момент процесса познания, диалектически связанный с истиной. Существует специфика логического подхода к понятию “ложь”. В двузначной логике отрицание истинного суждения дает ложное суждение и наоборот. Сложнее обстоит дело в многозначных логиках. В трехзначных логиках имеется три значения истинности: “истина”, “ложь”, “неопределенно”; при этом неистинное суждение может быть как ложным суждением, так и неопределенным. В т -значной логике Поста допускается т значений истинности, предельными из которых являются “истина” и “ложь”. В бесконечнозначной “Логике истины” Gхо между 1 и 0 лежит бесконечное число значений истинности. Автор построила бесконечнозначную систему “Логики лжи” - Fxo (от англ. false - ложь), которая отражает бесконечный процесс познания, идущий от незнания не к истине, а к заблуждению. В результате человек приходит к ложным суждениям - в юридической деятельности (неверно построенные версии в процессе расследования преступления), медицинской практике (постановка ошибочного диагноза), в научном творчестве (выдвижение ложных гипотез) и других сферах человеческой деятельности. Степень заблуждения бывает различной и может доходить до абсурда. Причем процесс возможного заблуждения потенциально бесконечен, что отражено в системе Fхо. Система Fхо имеет свою интерпретацию. Ее значения истинности отражают степень заблуждения, возникшего в результате либо умышленной дезинформации, либо незнания, либо неправильного истолкования результатов эксперимента, либо допущения логических ошибок, либо по другим причинам. Значениями истинности в “Логике лжи” являются: - 1 (ложь, заблуждение), 0 (незнание, отсутствие знания) и все дробные числа в интервале от 0 до - 1, построенные по определенной форме. То есть: - 1, - 1/2, - 1/4, - 3/4, - 1/8, - 1/16, - 15/16,.... - (1/2)k, - (1/2)k * ( 2 k - 1),..., 0 (где k - натуральное число). Логические операции в Fхо определены следующими равенствами: 1. Отрицание: [u x0 р ]= - 1- [ р ] = - (1+[ p ]) 2. Дизъюнкция: [ p 3. Конъюнкция: [ p & x0 q ]=min([ p ],[ q ]). 4. Импликация: [ р → p 5. Эквиваленция: [ р Тавтология (закон логики) принимает значение 0. Например, тавтологией является правило снятия двойного отрицания. Из бесконечнозначной системы Fхо вычленяются конечнозначные системы, F2,F3,F4,….. Fn. Закон исключенного третьего, закон непротиворечия и их отрицания в трехзначной “Логике лжи” (Fхо) не являются тавтологиями, ибо в колонках, соответствующих этим формулам, присутствуют значения или –1/2 или как –1/2, так как и - 1, а тавтологией является формула, принимающая лишь значение 0. Если эти законы не являются тавтологиями в трехзначной системе “Логика лжи”, то они не будут тавтологиями и в четырехзначной системе “Логика лжи” (F4) и в F5, и т. д. (т. е. в любой конечнозначной “Логике лжи”) и в бесконечнозначной “Логике лжи” Fхо. Система Fхо и другая построенная автором бесконечнозначная логика Gхо в совокупности охватывают оба направления в процессе познания - как в сторону истины, так и, к сожалению, в сторону лжи, заблуждения.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.113 (0.009 с.) |

 →х; 2) х
→х; 2) х 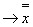 . Исходя из утверждения, что истинным является лишь второе, нидерландский логик и математик А. Рейтинг (1898-1980) разработал трехзначную пропозициональную логику. В этой логической системе импликация и отрицание отличаются от определений этих операций у Лукасевича лишь в одном случае. “Истина” обозначается 1, “ложь” - 0, “неопределенность” - 1/2. Тавтология принимает значение 1.
. Исходя из утверждения, что истинным является лишь второе, нидерландский логик и математик А. Рейтинг (1898-1980) разработал трехзначную пропозициональную логику. В этой логической системе импликация и отрицание отличаются от определений этих операций у Лукасевича лишь в одном случае. “Истина” обозначается 1, “ложь” - 0, “неопределенность” - 1/2. Тавтология принимает значение 1.
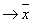 ), правила де Моргана и закон исключенного четвертого (x
), правила де Моргана и закон исключенного четвертого (x 
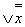 ) - тавтологии.
) - тавтологии. 2), где т -конечное число. Тавтологией является формула, которая всегда принимает выделенное значение, лежащее между 1 и т - 1, включая их самих.
2), где т -конечное число. Тавтологией является формула, которая всегда принимает выделенное значение, лежащее между 1 и т - 1, включая их самих. т- 1.
т- 1. 3 р
3 р  ), конъюнкция через (р.3 р), дизъюнкция - через
), конъюнкция через (р.3 р), дизъюнкция - через 3 q), эквиваленты - через (р
3 q), эквиваленты - через (р 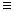 3 q).
3 q). х0 q ] = min([ p ],[ q j).
х0 q ] = min([ p ],[ q j). х0 q)
х0 q)  x0 q ]=max([ p ],[ q ]).
x0 q ]=max([ p ],[ q ]). x0 q ] = [(p → x0 q)& x0 (q → x0p)].
x0 q ] = [(p → x0 q)& x0 (q → x0p)].


