Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условно-разделительные (лемматические) умозаключения
Условно-разделительное умозаключение - это такое дедуктивное умозаключение, в котором одна посылка состоит из двух или большего числа условных суждении, а другая является разделительным суждением. В зависимости от числа членов в разделительной посылке это умозаключение может быть дилеммой (если разделительная посылка содержит два члена), трилеммой (если разделительная посылка содержит три члена) или вообще полилеммой (число разделительных членов больше двух). Дилемма Дилемма - условно-разделительное умозаключение, в котором одна посылка состоит из двух условных суждений, а другая является разделительным суждением, содержащим две альтернативы. Дилемма означает сложный, трудный для человека (или группы людей) выбор из двух нежелательных альтернатив - “из двух зол надо выбирать наименьшее”. Иногда говорят: “Альтернативы этому нет”, т. е. данному действию не может быть противоположного действия, иначе это приведет к краху. Дилеммы делятся на конструктивные и деструктивные. В свою очередь, те и другие подразделяются на простые и сложные. В простой конструктивной дилемме в первой (условной) посылке утверждается, что из двух различных оснований вытекает одно и то же следствие. Во второй посылке (дизъюнктивном суждении) утверждается, что одно или другое из этих оснований истинно. В заключении утверждается следствие. Пример: Если я пойду через речку по мосту, меня могут заметить; если я пойду через речку вброд, меня тоже могут заметить. Я могу идти через речку по мосту или вброд. ______________________________________ Меня могут заметить.
Соединив посылки знаком конъюнкции (“ л ”) и присоединив к ним посредством знака “->” заключение, мы получим формулу - этого вида дилеммы: ((а → b) ^ (с → b) ^ (а v с)) → b. Она выражает закон логики, т. е. является тождественно-истинной формулой. Сложная конструктивная дилемма отличается от простой только тем, что оба следствия ее первой (условной) посылки различны. Cхема Формула:
Этот вид дилеммы значительно чаще используют писатели, когда им необходимо подчеркнуть сложность коллизий реальной жизни, неоднозначность морального выбора. В рассказе Джека Лондона “Великая загадка” события происходят на севере Аляски. Вдова миллионера Карен Сейзер приехала, чтобы разыскать свою первую любовь Дэвида Пэйна. После долгих поисков она, наконец, разыскивает Дэвида Пэйна и умоляет его быть с ней. Перед героем стоит дилемма:
Если он согласится быть с ней (а), то он изменит своей жене - индианке, спасшей ему жизнь (b), если он не ответит на любовь белой женщины (с), то навсегда потеряет свою родину - юг Америки (d). Но он может согласиться быть с ней (a), или не ответить на любовь белой женщины (с). __ Он изменит своей жене - индианке, спасшей ему жизнь (b), или навсегда потеряет свою родину - юг Америки (d). Дэвид Пэйн остается с индианкой. Приведем еще пример дилеммы. Базарбай похитил из логова четырех волчат, продал их, а деньги пропил. Во время погони за волчицей Акбарой, утащившей его двухлетнего сына, Бостон рассуждает так: Если я выстрелю, то могу попасть в сына, а если я сейчас не выстрелю, то волчица утащит ребенка в свое логово. Я могу сейчас выстрелить или не стрелять. Я могу попасть в сына, или волчица утащит ребенка в свое логово. “И вот, наконец, похолодев, точно на дворе стояла стужа, он подбежал к волчице. И согнулся в три погибели, закачался, корчась в немом крике. Акбара была еще жива, а рядом с ней лежал бездыханный, с простреленной грудью малыш” (Ч. Айтматов. Плаха). В простой деструктивной дилемме первая (условная) посылка указывает на то, что из одного и того же основания вытекаютb два различных следствия. Во второй посылке содержится дизъюнкция отрицаний обоих этих следствий. В заключении отрицается основание. Схема этого вида умозаключения:
Формула может быть записана двумя способами: ((а→b)^ (а → с) ^ ( или ((а→ (b^ с)) ^ ( Главный герой романа Т. Драйзера “Американская трагедия” Клайд рассуждал так: Если я женюсь на Роберте (b), то меня ждет скучное существование (b) и для меня наступит полный крах (с). Я не хочу влачить скучное существование (b) или потерпеть полный крах (с).
Я не женюсь на Роберте (а). Сложная деструктивная дилемма отличается от простой только тем, что оба основания ее различны, заключение является дизъюнкцией отрицаний обоих оснований.
((а→ b) ^ (с→ d) ^ (
Студентам предлагается сформулировать дилемму на основе сюжета рассказа А. Конан Дойла “Женитьба бригадира”. “В конце концов объяснение стало неизбежным, и случилось это именно в тот вечер. Мари, несмотря на ее милое негодование, удалили в спальню, а я остался лицом к лицу со стариками, которые засыпали меня вопросами относительно моих намерений и видов на будущее. “Одно из двух, - сказали они с крестьянской прямотой, -или вы даете слово, что обручитесь с Мари, или вы ее никогда больше не увидите”. Я говорил о солдатском долге, о своих надеждах, о будущем, но они стояли на своем. Я ссылался на свою карьеру, а они эгоистично не хотели думать ни о чем, кроме своей дочери. Я оказался поистине в трудном положении. С одной стороны, я не мог отказаться от моей Мари, а с другой - к чему жениться молодому гусару? Наконец, когда меня уже совсем загнали в угол, я умолил их оставить все, как было, хотя бы до завтра”. Студенты должны выполнить творческое задание; найти в художественной литературе дилеммы или трилеммы; описать ситуацию, в которой происходит действие, затем четко сформулировать дилемму, проанализировать, какую из альтернатив принял человек и каким оказался результат его решения. Много различных дилемм стоит перед героями в детской литературе, перед персонажами сказок и басен. Приведем лишь некоторые примеры из книг для чтения в 1,2 и 3 классах. На многих из приводимых ниже дилемм акцентировали внимание учителя начальных классов средней школы № 356, слушавшие мой курс “Логика” и использовавшие эти дилеммы в своей работе с учащимися 1, 2, 3 классов. В рассказе Л. Н. Толстого “Фипипок. Быль” перед Филипком встала дилемма: “На Филипка нашел страх: “Что, как учитель меня прогонит?” И стал думать, что ему делать. Назад идти -опять собака заест, в школу идти - учителя боится... В школе Филипок так напугался, что говорить не мог... Филипок и рад бы что сказать, да в горле у него от страха пересохло”. Но все завершилось благополучно (Книга для чтения. Учебник для 1 класса. М, 1986. С. 279). В другом рассказе Л. Н. Толстого “Акула” (там же. С. 275) речь идет о том, что два мальчика с корабля, стоявшего у берегов Африки, купались в открытом море. “Вдруг с палубы кто-то крикнул “Акула!” - и все мы увидели в воде спину морского чудовища. Акула плыла прямо на мальчиков”. Артиллерист, отец одного из мальчиков, услышав их визг, “сорвался с места и побежал к пушкам. Он повернул хобот, прилег к пушке, прицелился и взял фитиль. Мы все, сколько нас было на корабле, замерли от страха и ждали, что будет. Раздался выстрел, и мы увидели, что артиллерист упал подле пушки и закрыл лицо руками... По волнам колыхалось желтое брюхо мертвой акулы”. Столь же напряженна и драматична ситуация, описанная Л. Н. Толстым в рассказе “Прыжок”. Мальчик вслед за обезьянкой забрался на мачту, затем “он пустил веревку и ступил на перекладину, покачивая руками, все замерли от страха. Стоило ему только оступиться - и он бы вдребезги разбился о палубу... В это время капитан корабля, отец мальчика, вышел из каюты. Он нес ружье, чтобы стрелять чаек. Он увидел сына на мачте и тотчас же прицелился в сына и закричал:
- В воду! Прыгай сейчас в воду! Застрелю! Мальчик шатался, но не понимал. - Прыгай или застрелю! Раз, два... - и как только отец крикнул: “три” - мальчик размахнулся головой вниз и прыгнул... Секунд через сорок - они долго показались всем - вынырнуло тело мальчика. Его схватили и вытащили на корабль. Через несколько минут у него изо рта и из носа полилась вода, и он стал дышать”. (Книга для чтения. Учебник для 2 класса. М., 1987. С. 212-213). Дилеммы сформулированы и в следующих рассказах (из книг для чтения). В рассказе “Честное слово” Л. Пантелеева мальчик в игре дал честное слово стоять, быть часовым, а ребята ушли, забыв о нем, и мальчик оказался поздно вечером один в саду, и только военный смог заставить мальчика “оставить пост”. Н. Артюхова в рассказе “Большая береза” описала переживания и поведение матери, увидевшей, какая опасность грозит сыну, взобравшемуся на большую березу: “Она смерила глазами расстояние от его ветки до земли, и лицо у нее стало почти такое же белое, как этот ровный березовый ствол”. Рассказ А. Гайдара “Совесть” начинается так: “Нина Карнаухова не приготовила уроков... и решила не идти в школу”. Решение дилемм, выбор одной из двух стоящих перед человеком альтернатив проходит иногда в острой борьбе, требующей мгновенного решения, и часто связан с нравственной позицией личности. Детские рассказы, описывающие дилеммы, помогают воспитывать лучшие моральные качества (совесть, ответственность, порядочность, обязательность и др.). Такова же роль и сказок, и басен. Из двух зол выбирай наименьшее, решай дилемму честным способом. Студентам первого курса МПГУ им. В. И. Ленина было предложено найти дилеммы в детской литературе, и одна студентка, Антонова Анна, которая только что окончила Московское педучилище № 15, где в течение двух лет изучала курс детской литературы, смогла привести 15 примеров дилемм из детской литературы. Не имея здесь возможности раскрыть ситуацию и четко сформулировать дилеммы, дадим ссылки на литературу (с указанием страниц), в которой их можно обнаружить: 1. Носов Н. Мишкина каша. М, 1977. С. 3. 2. Андерсен Г. X. Дикие лебеди. Сборник сказок. Минск, 1986. С. 283. 3. Андерсен Г. X. Свинопас. Там же. С. 274. 4. Перо Шарль. Рикки с хохолком. Там же. С. 9.
5. Толстой А. Приключения Буратино // Лукоморье. Сказки русских писателей. М., 1969. С. 476,487. 6. Киплинг Р. Маугли // Сборник сказочных повестей. М., 1985. С.22,48. 7. Гайдар А. Чук и Гек // Сочинения. М.-Л., 1948. С. 359. 8. Лагин Л. Старик Хоттабыч. Магадан, 1973. С. 110. 9. Волков А. Семь подземных королей // Сказочные повести. М.,1992. С. 249. 10. Волков А. Желтый туман. Там же. С. 460. Студентка первого курса Мельникова Лена, также только что закончившая музыкально-педагогическое училище, тоже привела много примеров дилемм из детской литературы. Перечислим некоторые из них: 1. Андерсен Г. X. Дюймовочка // Сказки, истории. М., 1973. С. 49. 2. Шварц Е. Сказка о потерянном времени. Цветик-семицветик // Сказки советских писателей. М., 1991. С. 184, 3. Милн Алан. Винни-Пух и все-все-все. М., 1985. С. 490. 4. Стивенсон Р. Л. Остров сокровищ. Л., 1977. С. 16. 5. Золушка // Сказки народов Югославии. М., 1991. С. 185. 6. Лагин Л. Старик Хоттабыч. М., 1973. С. 146. Мы надеемся, что вышеприведенные и многие другие дилеммы из детской литературы помогут студентам и учащимся средних педагогических учебных заведений интересно, эмоционально и с большим воспитательным эффектом изучить материал о дилеммах и о трилеммах (когда перед человеком возникает выбор не из двух, а из трех альтернатив, как, например, в народной сказке о путнике, стоящем на перекрестке трех дорог). Трилемма Трилеммы так же, как и дилеммы, могут быть конструктивными и деструктивными; каждая из этих форм в свою очередь может быть простой или сложной. Простоя конструктивная трилемма состоит из двух посылок и заключения; в первой посылке констатируется то, что из трех различных оснований вытекает одно и то же следствие; вторая посылка представляет собой дизъюнкцию этих трех оснований; в заключении утверждается следствие. Например: Если у больного грипп, то рекомендуется обратиться к врачу; если у больного острое респираторное заболевание, то рекомендуется обратиться к врачу; если у больного ангина, то рекомендуется обратиться к врачу. У данного больного или грипп, или острое респираторное заболевание, или ангина. Данному больному рекомендуется обратиться к врачу. В сложной конструктивной трилемме первая посылка состоит из трех различных оснований и трех различных вытекающих из них следствий, т. е. содержит три условных суждения. Вторая посылка является дизъюнктивным суждением, в котором утверждается (по крайней мере) одно из трех оснований. В заключении утверждается (по крайней мере) одно из трех следствий. Пример сложной конструктивной трилеммы. В некоторых сказках говорится о надписях на перекрестках трех дорог, которые содержат в себе, например, такого рода трилемму: Кто поедет прямо, будет в холоде и голоде; кто поедет направо, тот сам останется цел, а конь будет убит; кто поедет налево, тот сам будет убит, а конь останется цел. Человек может поехать либо прямо, либо направо, либо налево. Он или будет в холоде и голоде, или сам останется цел, а конь
будет убит, или сам будет убит, а конь останется цел.
Деструктивные трилеммы, так же как и деструктивные дилеммы, бывают простые и сложные. Структура их аналогична структуре дилеммы, только предусматривается не две, а три возможные альтернативы. Приведем пример простой деструктивной трилеммы: Если в ближайшее время погода ухудшится, то у него будут болеть суставы, повысится артериальное давление и будет ломить поясница. Известно, что у него или не болят суставы, или не повысилось артериальное давление, или не ломит поясница. В ближайшее время погода не ухудшится. В математике структура трилеммы используется тогда, когда возникают три возможных варианта решения задачи, доказательства теоремы и предстоит выбор одного из них.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.168.172 (0.045 с.) |

 ((а→b) ^ (с→ d) ^ (a v с)) → (b v d).
((а→b) ^ (с→ d) ^ (a v с)) → (b v d).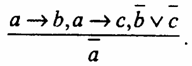
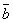
 )) → а
)) → а Схема: Формула:
Схема: Формула: )) → (
)) → (