
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Развитие логики в связи с проблемой обоснования математикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Немецкий математик и логик Готтлоб Фреге (1848-1925) предпринял попытку свести математику к логике. С этой целью в первой своей работе по математической логике “Исчисление понятий” (“Begriffsschrift”) он определил множество как объем понятия и таким образом получил возможность определить и число через объем понятия. Такое определение числа он сформулировал в “Основаниях арифметики” (“Grundlagen der Arithmetik”), книге, которая в то время осталась незамеченной, но впоследствии получила широкую известность. Здесь Фреге определяет число, принадлежащее понятию, как объем этого понятия. Два понятия считаются равночисленными, если множества, выражающие их объемы, можно поставить во взаимооднозначное соответствие друг с другом. Так, например, понятие “вершина треугольника” равночисленно понятию “сторона треугольника”, и каждому из них принадлежит одно и то же число 3, являющееся объемом понятия “вершина треугольника”. Если Лейбниц только наметил программу сведения математики к логике, то Г. Фреге предпринял попытку сведения довольно значительной части арифметики к логике, т. е. произвел некоторую математизацию логики'. Символические обозначения, принятые им, очень громоздки, и поэтому мало кто полностью прочитал его “Основные законы арифметики”. Впрочем, и сам Фреге особенно не рассчитывал на это. Тем не менее труд Фреге сыграл значительную роль в истории обоснования математики в первой половине XX в. Об этом своем произведении Фреге писал: “В моих “Основаниях арифметики” (1884) я пытался привести аргументы в пользу того, что арифметика есть часть логики и не должна заимствовать ни у опыта, ни у созерцания никаких основ доказательства. В этой книге (речь идет об “Основных законах арифметики - А. Г.) это должно быть подтверждено тем, что простейшие законы арифметики здесь выводятся только с помощью логических средств”2. Итак, Фреге полагал, что он логически определил число и точно перечислил логические правила, с помощью которых можно определять новые понятия и доказывать теоремы, и что таким образом он и сделал арифметику частью логики. Фреге не подозревал, однако, что построенная им система не только не представляла собой логического обоснования содержательной арифметики, но была даже противоречивой. Это противоречие в системе Фреге обнаружил Бертран Рассел. В послесловии к “Основным законам арифметики” Фреге писал по этому поводу: “Вряд ли есть что-нибудь более нежелательное для автора научного произведения, чем обнаружение по завершении его работы, что одна из основ его здания оказывается пошатнувшейся. В такое положение я попал, получив письмо от господина Бертрана Рассела, когда печатание этой книги близилось к концу”'. Противоречием, который обнаружил Рассел в системе Фреге, был знаменитый парадокс Рассела о множестве всех нормальных множеств (см. с. 226-227 учебника). Причину своей неудачи Фреге видел в использованном им предположении, что у всякого понятия есть объем в смысле постоянного, строго фиксированного множества, не содержащего в себе никакой неопределенности или расплывчатости. Ведь именно через этот объем он и определил основное понятие математики - понятие числа. Вслед за Г. Фреге очередную попытку сведения математики к логике предпринял видный английский философ и логик Бертран Рассел (1872-1970). Он также автор ряда работ из областей истории, литературы, педагогики, эстетики, естествознания, социологии и др. Труды Рассела по математической логике оказали большое влияние на ее развитие. Вместе с английским логиком и математиком А. Уайтхедом2 Рассел разработал оригинальную систему символической логики в фундаментальном трехтомном труде “Principia Mathematica”3. Выдвигая идею сведения математики к логике, Рассел считает, что если гипотеза относится не к одной или нескольким частным вещам, но к любому предмету, то такие выводы составляют математику. Таким образом, он определяет математику как доктрину, в которой мы никогда не знаем ни того, о чем мы говорим, ни того, верно ли то, что мы говорим. Рассел делит математику на чистую и прикладную. Чистая математика, по его мнению, есть совокупность формальных выводов, независимых от какого бы то ни было содержания, т. е. это класс высказываний, которые выражены исключительно в терминах переменных и только логических констант. Рассел не только вполне уверен в том, что ему удалось свести математику к такого рода предложениям, но делает из этого утверждения вывод о существовании априорного знания, считает, что “математическое познание нуждается в посылках, которые не базировались бы на данных чувства”'. От чистой математики Рассел отличает прикладную математику, которая состоит в применении формальных выводов к материальным данным. Для того чтобы показать, что чистая математика сводится к логике, Рассел берет систему аксиом арифметики, сформулированную Пеано, и пытается их логически доказать, а три неопределяемые у Пеано понятия: “нуль”, “число”, “следующее за” - определить в терминах своей логической системы. Все натуральные числа Рассел также считает возможным выразить в терминах логики, а следовательно, свести арифметику к логике. А так как, по его мнению, вся чистая математика может быть сведена к арифметике, то математика может быть сведена к логике. Рассел пишет: “Логика стала математической, математика логической. Вследствие этого сегодня совершенно невозможно провести границу между ними. В сущности это одно и то же. Они различаются, как мальчик и мужчина; логика - это юность математики, а математика - это зрелость логики”2. Рассел считает, что не существует пункта, где можно было бы провести резкую границу, по одну сторону которой находилась бы логика, а по другую - математика. Но в действительности математика несводима к логике. Предметы изучения этих наук различны. Нами ранее были указаны характерные черты, присущие логике как науке (см. с.141-142). У математики другие задачи и функции. В большом труде “Principia Mathematica” есть две стороны. Первая - заставляющая видеть в нем один из основных истоков современной математической логики. Все, что связано с этой стороной Principia Mathematica, получило в дальнейшем такое развитие в математической логике, которое сделало эту новую область науки особенно важной для решения не только труднейших задач теоретической математики и ее обоснования, но и целого ряда весьма важных для практики задач вычислительной математики и техники. Другая сторона этого произведения - точнее, даже не самого этого произведения, а философских “обобщений”, делаемых логицистами со ссылкой на него, - принадлежит уже к области попыток использовать его для “доказательства” положения, что математика-де сводится к логике. Именно эта сторона сомнительна, и ее опровергает дальнейшее развитие науки, которое обнаружило, что попытка Рассела безуспешна. И это не случайно. Дело не в том, что Рассел в каком-то смысле не совсем удачно построил свою систему. Дело в том, что вообще нельзя построить формальную “логическую систему” с точно перечисленными и эффективно выполнимыми правилами вывода, в которой можно было бы формализовать всю содержательную арифметику. Это обстоятельство представляет собой содержание известной теоремы австрийского математика и логика К. Гёделя о неполноте формализованной арифметики', из которой следует непосредственно, что определение математических понятий в терминах логики хотя и обнаруживает некоторые их связи с логикой, тем не менее не лишает их специфически математического содержания. Формализованная система имеет смысл лишь при наличии содержательной научной теории, систематизацией которой данная формализованная система должна служить. Однако Г. Фреге и Б. Рассел в своем логическом анализе пришли к ряду интересных результатов, относящихся к понятиям “предмет”, “имя”, “значение”, “смысл”, “функция”, “отношение” и др. Особо следует подчеркнуть значение разработанной Расселом теории типов (простой и разветвленной), цель которой состоит в том, чтобы помочь разрешить парадоксы в теории множеств. Рациональное зерно разветвленной теории Рассела состоит в том, что она является конструктивной теорией. Одним из оснований деления логики служит различие применяемых в ней принципов, на которых базируются исследования. В результате такого деления имеем классическую логику и неклассические логики. В. С. Меськов выделяет такие основополагающие принципы классической логики: “1) область исследования составляют обыденные рассуждения, рассуждения в классических науках; 2) допущение о разрешимости любой проблемы; 3) отвлечение от содержания высказываний и от связей по смыслу между ними; 4) абстракция двузначности высказываний”'., Неклассические логики отступают от этих принципов. К ним относятся интуиционистская логика, конструктивные логики, многозначные, модальные, положительные, паранепротиворечи-вые и другие логики, к изложению которых мы переходим.
Интуиционистская логика Интуиционистская логика построена в связи с развитием интуиционистской математики. Интуиционистская школа основана в 1907 г. голландским математиком и логиком Л. Брауэром (1881-1966)2, но некоторые ее идеи выдвигались и ранее. Интуиционизм - философское направление в математике и логике, отказывающееся от использования абстракции актуальной бесконечности, отвергающее логику как науку, предшествующую математике, и рассматривающее интуитивную ясность и убедительность (“интуицию”) как последнюю основу математики и логики. Интуиционисты свою интуиционистскую математику строят с помощью финитных (конечных) средств на основе системы натуральных чисел, которая считается известной из интуиции. Интуиционизм включает в себя две стороны - философскую и математическую. Математическое содержание интуиционизма изложено в ряде работ математиков. Ведущие представители отечественной школы конструктивной математики отмечают положительное значение некоторых математических идей интуиционистов. В целом конструктивная математика существенно отличается от интуиционистской, но, как указывал советский математик-конструктивист А. А. Марков, конструктивное направление имеет точки соприкосновения с интуиционистской математикой. Конструктивисты сходятся с интуиционистами в понимании дизъюнкции и в силу этого признают правильной данную Брауэром критику закона исключенного третьего. Вместе с тем конструктивисты считают неприемлемыми методологические основы интуиционизма. Если математический аспект интуиционизма имеет рациональный смысл (в этой связи предпочтительнее говорить об интуиционистской математике или интуиционистской логике, а не об интуиционизме), то второй его аспект - философско-методологический - совершенно неприемлем. Брауэр считал, что чистая математика представляет собой свободное творение разума и не имеет никакого отношения к опытным фактам. У интуиционистов единственным источником математики оказывается интуиция, а критерием приемлемости математических понятий и выводов является “интуитивная ясность”. Но интуиционист Гейтинг вынужден был признаться в том, что понятие интуитивной ясности в математике само не является интуитивно ясным; можно даже построить нисходящую шкалу степеней очевидности. Основой происхождения математики в конечном итоге является не какая-то “интуитивная ясность”, а отражение в сознании пространственных форм и количественных отношений действительного мира. Гейтинг, как и Брауэр, в гносеологии субъективный идеалист. Он считает, что математическая мысль не выражает истину о внешнем мире, а связана исключительно с умственными построениями'. Еще в 1936 г. советский математик А.Н. Коломогоров подверг критике субъективно-идеалистические основы интуиционизма, заявив, что невозможно согласиться с интуиционистами, когда они говорят, что математические объекты являются продуктом конструктивной деятельности нашего духа, ибо математические объекты являются абстракциями реально существующих форм независимой от нашего духа действительности. Интуиционисты не признают практику и опыт источником формирования математических понятий, методов математических построений и методов доказательств. Особенности интуиционистской логики вытекают из характерных признаков интуиционистской математики. В современной классической математике часто прибегают к косвенным доказательствам. Но их почти невозможно ввести в интуиционистскую математику и логику, так как там не признаются закон исключенного третьего и закон Закон исключенного третьего для бесконечных множеств в интуиционистской логике не проходит потому, что р Эта знаменитая проблема X. Гольдбаха была поставлена им в 1742 г. и не поддавалась решению около 200 лет. Гольдбах высказал предположение, что всякое целое число, большее или равное шести, может быть представлено в виде суммы трех простых чисел. Для нечетных чисел это предположение было доказано только в 1937 г. советским математиком академиком И. М.Виноградовым; все достаточно большие нечетные числа представимы в виде суммы трех простых чисел. Это - одно из крупнейших достижений современной математики. Брауэр первый наметил контуры новой логики. Идеи Брауэра формализовал Гейтинг, в 1930 г. построивший интуиционистское исчисление предложений с использованием импликации, конъюнкции, дизъюнкции и отрицания на основе 11 аксиом и двух правил вывода - modus ponens и правила подстановки. Гейтинг утверждает, что хотя основные различия между классической и интуиционистской логиками касаются свойств отрицания, эти логики не совсем совпадают и в формулах без отрицания. Он отличает математическое отрицание от фактического: первое выражается в форме конструктивного построения (выполнения) определенного действия, а второе говорит о невыполнении действия (“невыполнение” чего-либо не является конструктивным действием). Интуиционистская логика имеет дело только с математическими суждениями и лишь с математическим отрицанием, которое определяется через понятие противоречия, а понятие противоречия интуиционисты считают первоначальным, выражающимся или приходящимся в форме 1 = 2. Фактическое отрицание не связано с понятием противоречия. Проблемами интуиционистской логики занимаются также философы К. Н. Суханов, М. И. Панов, А. Л. Никифоров и др. Конструктивные логики Конструктивная логика, отличная от логики классической, своим рождением обязана конструктивной математике. Конструктивная математика может быть кратко охарактеризована как абстрактная умозрительная наука о конструктивных процессах и нашей способности их осуществлять. В результате конструктивного процесса возникает конструктивный объект, т. е. такой объект, который задается эффективным (точным и вполне понятным) способом построения (алгоритмом). Конструктивное направление (в математике и логике) ограничивает исследование конструктивными объектами и проводит его в рамках абстракции потенциальной осуществимости (реализуемости), т. е. игнорирует практическое ограничение наших возможностей построений в пространстве, времени, материале. Между идеями конструктивной логики советских исследователей и некоторыми идеями интуиционистской логики (например, в понимании дизъюнкции, в отказе от закона исключенного третьего) имеются точки соприкосновения. Однако между конструктивной и интуиционистской логиками имеются и существенные отличия. 1. Различные объекты исследования. В основу конструктивной логики, которая является логикой конструктивной математики, положена абстракция потенциальной осуществимости, а в качестве объектов исследования допускаются лишь конструктивные объекты (слова в определенном алфавите). В основу интуиционистской логики, которая является логикой интуиционистской математики, положена идея “свободно становящейся последовательности”, т. е. строящейся не по алгоритму, которую интуиционисты считают интуитивно ясной. 2. Обоснование интуиционистской математики и логики дается с помощью идеалистически истолкованной интуиции, а обоснование конструктивной математики и логики дается на базе математического понятия алгоритма (например, нормального алгоритма А. А. Маркова) или эквивалентного ему понятия рекурсивной функции. 3. Различные методологические основы. Методологической основой конструктивного направления в математике является признание практики источником познания и критерием его истинности (в том числе и научного). Это положение сохраняет свою силу и для таких наук, как логика и математика, хотя здесь практика входит в процесс познания лишь опосредованно, в конечном счете. Интуиционисты же считают источником формирования математических понятий и методов первоначальную “интуицию”, а критерием истинности в математике - “интуитивную ясность”. 4. Различные интерпретации 1. А. Н. Колмогоров интерпретировал интуиционистскую логику как исчисление задач. А. А. Марков интерпретировал логические связки конструктивной логики как прилагаемые к потенциально осуществимым конструктивным процессам (действиям). Интуиционистская логика Л. Брауэра и А. Рейтинга интерпретируется ими как исчисление предложений (высказываний), причем область высказываний у них ограничивается математическими предложениями. 5. Отличие ряда логических средств. Представители узко-конструктивной логики признают в качестве принципа: если имеется алгоритмический процесс и удалось опровергнуть, что он продолжается бесконечно, то, следовательно, процесс закончится. Некоторые из представителей конструктивной логики доказывают этот принцип в уточненной форме. Представители интуиционистской логики не признают данного принципа. Конструктивные исчисления высказываний В. И. Гливенко и А. Н. Колмогорова Первыми представителями конструктивной логики были математики А. Н. Колмогоров (1903-1987) и В. И. Гливенко (1897-1940). Первое исчисление, не содержащее закон исключенного третьего, было предложено в 1925 г. А. Н. Колмогоровым в связи с его критикой концепции Л. Брауэра, а в дальнейшем развито В. И. Гливенко. Позже было опубликовано исчисление Гейтинга, которое Колмогоров интерпретировал как исчисление задач, что породило содержательное истолкование исчислений, не пользующихся законом исключенного третьего, а это, в свою очередь, легло в основу всех дальнейших, подлинно научных исследований таких исчислений. Введя понятия “псевдоистинность” (двойное отрицание суждения) и “псевдоматематика” (“математика псевдоистинности”), Колмогоров доказал, что всякий вывод, полученный с помощью закона исключенного третьего, верен, если вместо каждого суждения, входящего в его формулировку, поставить суждение, утверждающее его двойное отрицание. Тем самым он показал, что в “математике псевдоистинности” законно применение принципа исключенного третьего. Колмогоров различает две логики суждений – общую и частную. Различие между ними заключается в одной аксиоме Какова же область применения частной логики суждений? Все ее формулы верны для суждения типа А., в том числе для всех финитных и для всех отрицательных суждений, т. е. область применимости ее совпадает с областью применимости формулы двойного отрицания
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 689; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.228.195 (0.016 с.) |

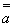 >а и которые участвуют в косвенных доказательствах. Но закон непротиворечия представители как интуиционистской, так и конструктивной логики считают неограниченно применимым.
>а и которые участвуют в косвенных доказательствах. Но закон непротиворечия представители как интуиционистской, так и конструктивной логики считают неограниченно применимым.
 требует общего метода, который по произвольному высказыванию р позволил бы получать доказательство, либо доказательство отрицания. Гейтинг считает, что так как интуиционисты не располагают таким методом, то они не вправе утверждать и принцип исключенного третьего. Покажем это на таком примере. Возьмем утверждение: “Всякое целое число, большее единицы, либо простое, либо сумма двух простых, либо сумма трех простых”. Неизвестно, так это или не так в общем случае, хотя в рассмотренных случаях, которых конечное число, это так. Существует ли число, которое не удовлетворяет этому требованию? Мы не можем указать такое число и не можем вывести противоречие из допущения его существования.
требует общего метода, который по произвольному высказыванию р позволил бы получать доказательство, либо доказательство отрицания. Гейтинг считает, что так как интуиционисты не располагают таким методом, то они не вправе утверждать и принцип исключенного третьего. Покажем это на таком примере. Возьмем утверждение: “Всякое целое число, большее единицы, либо простое, либо сумма двух простых, либо сумма трех простых”. Неизвестно, так это или не так в общем случае, хотя в рассмотренных случаях, которых конечное число, это так. Существует ли число, которое не удовлетворяет этому требованию? Мы не можем указать такое число и не можем вывести противоречие из допущения его существования.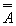 → А, которая имеется лишь среди аксиом частной логики. Интересна диалектика соотношения содержания и областей применения этих логик: содержание частной логики суждений богаче, чем общей, так как частная логика дополнительно включает аксиому
→ А, которая имеется лишь среди аксиом частной логики. Интересна диалектика соотношения содержания и областей применения этих логик: содержание частной логики суждений богаче, чем общей, так как частная логика дополнительно включает аксиому 


