Законы логики и их роль в познании

Этот закон формулируется так: “В процессе определенного рассуждения всякое понятие и суждение должны быть тождественны самим себе”.

В математической логике закон тождества выражается следующими формулами:

а = а (в логике высказываний) и

А = А (в логике классов, в которой классы отождествляются с объемами понятий).

Тождество есть равенство, сходство предметов в каком-либо отношении. Например, все жидкости тождественны в том, что они теплопроводны, упруги. Каждый предмет тождествен са­мому себе. Но реально тождество существует в связи с разли­чием. Нет и не может быть двух абсолютно тождественных вещей (например, двух листочков дерева, близнецов и т. д.). Вещь вчера и сегодня и тождественна, и различна. Например, внеш­ность человека изменяется с течением времени, но мы его уз­наем и считаем одним и тем же человеком. Абстрактного, аб­солютного тождества в действительности не существует, но в определенных границах мы можем отвлечься от существую­щих различий и фиксировать свое внимание на одном только тождестве предметов или их свойств.

В мышлении закон тождества выступает в качестве норматив­ного правила (принципа). Он означает, что нельзя в процессе рас­суждения подменять одну мысль другой, одно понятие - другим. Нельзя тождественные мысли выдавать за различные, а различ­ные - за тождественные.

Например, тождественными по объему будут три такие поня­тия: “ученый, по инициативе которого был основан Московский университет”; “ученый, сформулировавший принцип сохранения материи и движения”; “ученый, ставший с 1745 г. первым русским академиком Петербургской академии” - все они обозна­чают одного и того же человека (М. В. Ломоносова), но дают различную информацию о нем.

Нарушение закона тождества приводит к двусмысленностям, что можно видеть, например, в следующих рассуждениях: “Ноздрев был в некотором отношении исторический человек. Ни на одном собрании, где он был, не обходилось без иcmopuu” (H. В. Гоголь). “Стремись уплатить свой долг, и ты достигнешь двоякой цели, ибо тем самым его исполнишь” (Козьма Прутков). Игра слов в этих примерах построена на употреблении омонимов.

В мышлении нарушение закона тождества проявляется тогдa, когда человек выступает не по обсуждаемой теме, произвольно подменяет один предмет обсуждения другим, употребляет термины и понятия в другом смысле, чем принято, не предупреждая об этом. Например, идеалистом иногда считают (человека, верящего в идеалы, живущего ради высокой цели, а материалистом - человека меркантильного, стремящегося к наживе, к личному обогащению и т. д.

На дискуссиях иногда спор по существу подменяют спором о:ловах. Иногда люди говорят о разных вещах, думая, что они имеют в виду одно и то же. Часто логическая ошибка наблюда­ется, когда люди употребляют слова-омонимы, т. е. слова, имею­щие несколько значений, например, “следствие”, “материя”, “содержание” и др. Возьмем, к примеру, высказывание: “Учени­ки прослушали разъяснения учителя”. Здесь неясно, слушали ли они внимательно учителя или, наоборот, пропустили его разъяс­нения. Или: “Из-за рассеянности шахматист не раз на турнирах терял очки”. Здесь неизвестно, о каких очках идет речь. Иногда ошибка возникает при использовании личных местоимений: она, оно, мы и др., когда приходится уточнять: “Кто - он?” или “Кто -она?”. В результате отождествления различных понятий возника­ет логическая ошибка, называемая подменой понятия.

Из-за нарушения закона тождества возникает и другая ошиб­ка, называемая подменой тезиса. В ходе доказательства или опровержения выдвинутый тезис часто умышленно или неосоз­нанно подменяется другим. В научных и иных дискуссиях это проявляется в приписывании оппоненту того, чего он не говорил. Такие приемы ведения дискуссий недопустимы.

Прием подмены тезиса: вместо одного вопроса стремятся искусно подсунуть другой, чтобы отвлечь в нужный момент вни­мание читателя, наговорив кучу к делу не относящихся вещей, приписать оппоненту то, чего он не говорил, и т. д.

Отождествление (или идентификация) широко используется в следственной практике, например, при опознании предметов, людей, отождествлении почерков, документов, подписей на доку­менте, отождествлении отпечатков пальцев.

Закон тождества используется в науке, искусстве, в програм­мах для работы на ЭВМ, в школьном преподавании, в повсе­дневной жизни.

В науках существуют различные виды и модификации тож­дества. Например, в математике это равенство, эквивалент­ность (равномощность, равночисленность) множеств, конгру­энтность, тождественное преобразование, тождественная подстановка и т. д.; в теории алгоритмов - одинаковость букв, устанавливаемая путем абстракции отождествления, равенст­во алфавитов (А = В), равенство конкретных слов и т. д.

Равенства обладают свойствами рефлексивности (а = а), симметричности (если а = b,то

b = а) и транзитивности (если а = b и b = с, то а = с). К равенствам применимо правило замены равного равным.

Закон непротиворечия

Если предмет А обладает определенным свойством, то в суж­дениях об А люди должны утверждать это свойство, а не отрицать его. Если же человек, утверждая что-либо, отрицает то же самое или утверждает нечто несовместимое с первым, налицо логичес­кое противоречие. Формально-логические противоречия - это про­тиворечия путаного, неправильного рассуждения. Такие противо­речия затрудняют познание мира.

Древнегреческий философ и ученый Аристотель считал “са­мым достоверным из всех начал” следующее: “...Невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении”'. Эта формули­ровка указывает на необходимость для человека не допускать в своем мышлении и речи формально-противоречивые высказыва­ния, в противном случае его мышление будет неправильным.

Мысль противоречива, если мы об одном и том же предмете в одно и то же время и в одном и том же отношении нечто ут­верждаем и то же самое отрицаем. Например: “Кама - приток Волги” и “Кама не является притоком Волги”. Или: “Лев Тол­стой - автор романа “Воскресение” и “Лев Толстой не является автором романа “Воскресение”.

Противоречия не будет, если мы говорим о разных предметах или об одном и том же предмете, взятом в разное время или в разном отношении. Противоречия не будет, если мы скажем:

“Осенью дождь полезен для грибов” и “Осенью дождь не полезен для уборки урожая”. Суждения “Этот букет роз свежий” и “Этот букет роз не является свежим” также не противоречат друг другу, ибо предметы мысли в этих суждениях берутся в разных отношениях или в разное время. Суждения “Саша Голубев не является перворазрядником по бегу” и “Саша Голубев является перворазрядником по бегу” не будут противоречащи­ми, если они не относятся к одному и тому же времени.

Не могут быть одновременно истинными следующие четыре типа простых суждений:

1. “Данное S есть Р” и “Данное S не есть Р”.

2. “Ни одно S не есть Р” и “Все S есть Р”.

3. “Все S есть Р” и “Некоторые S не есть Р”.

4. “Ни одно S не есть Р” и “Некоторые S есть Р”.

При этом вторая пара суждений такова, что оба суждения могут быть ложными, например: “Ни один студент не является спортсменом” и “Все студенты являются спортсменами”.

Чаще всего встречается определение формально-логического противоречия как конъюнкции суждения и его отрицания (а и не а). Но логическое противоречие может быть выражено и без отрица­ния: оно имеет место между несовместимыми и утвердительными суждениями1.

Закон непротиворечия не действует в логике “размытых” (fuzzy) множеств, ибо в ней к “размытым” множествам и “размытым” алгоритмам можно одновременно применять ут­верждение и отрицание (например: “Этот мужчина пожилой” и “Этот мужчина еще не является пожилым”, ибо понятие “пожи­лой мужчина” является “нечетким” понятием, не имеющим чет­ко очерченного объема).

Приведенные примеры свидетельствуют о том, что формально­логическое противоречие возникает тогда, когда пытаются счи­тать истинными два или несколько утвердительных суждений, не совместимых между собой. Не менее распространенной в мышле­нии является форма логического противоречия, когда одновременно утверждается и отрицается одно и то же суждение, т. е. допуска­ется конъюнкция а и не-а. Таким образом, в традиционной фор­мальной логике противоречием считается утверждение двух противоположных (как контрарных, так и контрадикторных) суж­дений об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении. В исчислении высказываний клас­сической двузначной логики закон непротиворечия записывается следующей формулой:

a ^ a

 

Закон непротиворечия читается так: “Два противоположных суждения не могут быть истинными в одно и то же время и в одном и том отношении”. К противоположным суждениям относятся: 1) противные (контрарные) суждения А и Е, которые оба могут быть ложными, поэтому не являются отрицающими друг друга, и их нельзя обозначить как а и a; 2) противоречащие [контрадикторные) суждения А и О, Е и I, а также единичные суждения “Это S есть Р” и “Это S не есть Р”, которые являются отрицающими, так как если одно из них истинно, то другое обязательно ложно, поэтому их обозначают а и a.

Формула закона непротиворечия в двузначной классической логике a ^ a отражает лишь часть содержательного аристотелев­ского закона непротиворечия, так как она относится только к проти­воречащим суждениям (а и не-а) и не распространяется на противные (контрарные суждения). Поэтому формула а^a неадекватно, нe полностью представляет содержательный закон непротиворечия. Следуя традиции, мы за формулой a ^ a сохраняем название “закон непротиворечия”, хотя оно значительно шире, чем данная формула.

Если в мышлении (и речи) человека обнаружено формально-логическое противоречие, то такое мышление считается неправильным, а суждение, из которого вытекает противоречие, отрицается и считается ложным. Поэтому в полемике при опровержении мнения оппонента широко используется метод “приведения к абсурду”.

Диалектические противоречия процесса познания выражаются в форме (структуре) формально-логических противоречий, напримep: опровержение гипотезы путем опровержения (фальсифика­ции) следствий, противоречащих опытным фактам или ранее известным законам; выступления докладчика и оппонента, обвинителя и защитника; взгляды людей, придерживающихся конкурируюших гипотез; мышление врача (или врачей при консилиуме), получившего клинические анализы, несовместимые с ранee поставленным диагнозом болезни. Во всех этих и подобных (м ситуациях фиксируется несовместимость суждения а и не-а, например, несовместимость какого-либо суждения а из прежней теории и суждения не-а, выражающего мысль о новом получен­ном опытном факте, т. е. фиксируется мысль, что суждения а и не-а не могут быть оба истинными, и поэтому их конъюнкция ложна. Отсюда (по законам классической двузначной логики) де­лается вывод, что требуется дальнейшее исследование, анализ.

Итак, первичным (содержанием) выступает диалектическое противоречие, объективно возникающее в процессе познания, и именно оно служит движущей силой познания, а вторичным яв­ляется способ фиксации (способ выражения) диалектического противоречия в виде конъюнкции двух суждений а и не-а, т. е. в форме формально-логического противоречия.

Здесь налицо ситуация, по своему типу аналогичная случаю “антиномии-проблемы”, когда возникшее диалектическое противоречие в познании до момента его разрешения выража­ется в форме “а и не-а”, т. е. принимает как бы облик, оболо­чку, внешнюю форму формально-логического противоречия, а по существу остается диалектическим противоречием, требу­ющим своего разрешения в ходе исследования возникшей про­блемы. В результате диалектического синтеза тезиса и антитезиса получается новое знание, отличающееся как от тезиса, так и от антитезиса, а также не являющееся их конъ­юнкцией. Итак, в мышлении диалектическое противоречие до его разрешения принимает форму (структуру) формально-ло­гического противоречия, а обнаружение последнего свидетель­ствует или “сигнализирует” о том, что необходим дальнейший анализ и исследование возникшей в познании ситуации. Разре­шение обнаруженного диалектического противоречия способ­ствует продвижению познания. Одним из примеров антиномий1 является формулировка познавательной задачи в первом томе “Капитала” К. Маркса, где он пишет: “...Капитал не может воз­никнуть из обращения и так же не может возникнуть вне обра­щения. Он должен возникнуть в обращении и в то же время не в обращении”.

Закон исключенного третьего

Онтологическим аналогом этого закона является то, что в предмете указанный признак присутствует или его нет, поэтому и в мышлении мы отражаем это обстоятельство в виде закона исключенного третьего.

В книге “Метафизика” Аристотель сформулировал закон ис­ключенного третьего так: “Равным образом не может быть ни­чего промежуточного между двумя членами противоречия, а относительно чего-то одного необходимо что бы то ни было одно либо утверждать, либо отрицать”1.

В двузначной традиционной логике закон исключенного треть­его формулируется так: ”Из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано”. Проти­воречащими (контрадикторными) называются такие два суж­дения, в одном из которых что-либо утверждается о предмете, а в другом то же самое об этом же предмете отрицается, поэто­му они не могут быть оба одновременно истинными и оба лож­ными; одно из них истинно, а другое обязательно ложно. Такие суждения называются отрицающими друг друга. Если одно из противоречащих суждений обозначить переменной а, то другое следует обозначить a. Так, из двух суждений: “Джеймс Фенимор Купер является автором серии романов о Кожаном Чулке, сдававшихся на протяжении почти 20 лет” и “Джеймс Фенимор Купер не является автором серии романов о Кожаном Чулке, создававшихся на протяжении почти 20 лет” первое истинно, второе ложно, и третьего - промежуточного - суждения не может быть.

Отрицающими являются следующие пары суждений:

1) “Это S есть Р” и “Это S не есть Р” (единичные суждения).

2) “Все S есть Р” и “Некоторые S не есть Р” (суждения А и О).

3) “Ни одно S не есть Р” и “Некоторые S есть Р” (суждения Е и І).

В отношении противоречащих (контрадикторных) суждений (А и О, Е и I) действует как закон исключенного третьего, так и закон непротиворечия - в этом одно из сходств данных законов.

Различие в областях определения (т. е. применения) этих зако­нов в том, что по отношению противных (контрарных) суждений А и Е (например: “Все грибы - съедобны” и “Ни один гриб не является съедобным”), которые оба не могут быть истинными, но оба могут быть ложными, распространяется действие лишь закона непротиворечия и не распространяется действие закона исключенного третьего. Итак, сфера действия содержательно­го закона непротиворечия шире (это контрарные и контрадик­торные суждения), чем сфера действия содержательного зако­на исключенного третьего (лишь контрадикторные, т. е. суждения типа а и не-а). Действительно, истинно одно из двух суждений:

“Все дома в данной деревне электрифицированы” или “Некото­рые дома в данной деревне не являются электрифицированными” и третьего не дано.

Закон исключенного третьего и в содержательном, и в форма­лизованном виде охватывает один и тот же круг суждений -противоречащие, т. е. отрицающие друг друга.

Содержательные аристотелевские законы непротиворечия и исключенного третьего невыводимы один из другого, так как области определения суждений, для которых они применимы, различные.

В силу того, что в формализованных законах непротиворечия и исключенного третьего, т. е. в формулах и а v a, области определения пропозициональных переменных (т. е. переменных, обозначающих суждение и его отрицание: а и a) оказываются одними и теми же (берутся лишь противоречащие суждения), то на основании закона де Моргана, т. е. формулы в = 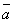v 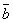, за­кона снятия двойного отрицания, т. е. a s а и закона коммута­тивности дизъюнкции, т. е. формулы (а v b) = (b v а), в двузнач­ной классической логике, путем элементарных эквивалентных преобразований из закона непротиворечия можно вывести закон исключенного третьего (и наоборот):

 

В мышлении закон исключенного третьего предполагает чет­кий выбор одной из двух взаимоисключающих альтернатив. Для корректного ведения дискуссии выполнение этого требования обязательно.