
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямое и непрямое (косвенное) доказательстваСодержание книги
Поиск на нашем сайте
Доказательства по форме делятся на прямые и непрямые (косвенные). Прямое доказательство идет от рассмотрения аргументов к доказательству тезиса, т. е. истинность тезиса непосредственно обосновывается аргументами. Схема этого доказательства такая: из данных аргументов (а, b, с,...) необходимо следует доказываемый тезис q. По этому типу проводятся доказательства в судебной практике, в науке, в полемике, в сочи нениях школьников, при изложении материала учителем и т. д. Широко используется прямое доказательство в статистических отчетах, в различного рода документах, в постановлениях, в художественной и другой литературе. Приведем пример прямого доказательства, использованного И. А. Буниным в стихе творении “В степи”: А к нам идет угрюмая зима: Засохла степь, лес глохнет и желтеет, Осенний ветер, тучи нагоняя, Открыл в кустах звериные лазы, Листвой засыпал долы и овраги, И по ночам в их черной темноте, Под шум деревьев, свечками мерцают, Таинственно блуждая, волчьи очи... Да, край родной не радует теперь! Чтобы обосновать тезис: “Труд доктора - действительно самый производительный труд”, Н. Г. Чернышевский использует прямое доказательство с помощью таких аргументов: предохраняя или восстанавливая здоровье, доктор приобретает обществу все те силы, которые погибли бы без его забот. Учитель на уроке при прямом доказательстве тезиса “Народ -творец истории”, показывает; во-первых, что народ является создателем материальных благ, во-вторых, обосновывает огромную роль народных масс в политике, разъясняет, как в современную эпоху народ ведет активную борьбу за мир и демократию, в-третьих, раскрывает его большую роль в создании духовной культуры. На уроках химии прямое доказательство о горючести сахара может быть представлено в форме категорического силлогизма: Все углеводы - горючи. Сахар - углевод. Сахар горюч. В современном журнале мод “Бурда” тезис “Зависть - корень всех зол” обосновывается с помощью прямого доказательства следующими аргументами: “Зависть не только отравляет людям повседневную жизнь, но может привести и к более серьезным последствиям, поэтому наряду с ревностью, злобой и ненавистью, несомненно, относится к самым плохим чертам характера. Подкравшись незаметно, зависть ранит больно и глубоко. Человек завидует благополучию других, мучается от сознания того, что кому-то более повезло”'. Непрямое (косвенное) доказательство - это доказательство, в котором истинность выдвинутого тезиса обосновывается путем доказательства ложности антитезиса. Если тезис об значить буквой а, то его отрицание ( Апагогическое косвенное доказательство (или доказательство “от противного”) осуществляется путем ycтановления ложности противоречащего тезису суждения. Этот метод часто используется в математике. Пусть а -тезис или теорема, которую надо доказать. Предполагаем от противного, что а ложно, т. е. истинно не-а (или Следует заметить, что в конструктивной логике формула Разделительное доказательство (методом исключения). Антитезис является одним из членов разделительного суждения, в котором должны быть обязательно перечислены все возможные альтернативы, например: Преступление мог совершить либо А, либо В, либо С. Доказано, что не совершали преступление ни А, ни В. Преступление совершил С. Истинность тезиса устанавливается путем последовательного доказательства ложности всех членов разделительного суждения, кроме одного. Здесь применяется структура отрицающе-утверждающего модуса разделительно-категорического силлогизма. Заключение будет истинным, если в разделительном суждении предусмотрены все возможные случаи (альтернативы), т. е. если оно является закрытым (полным) дизъюнктивным суждением: a d Как отмечалось ранее, в этом модусе союз “или” может употребляться и как строгая дизъюнкция (\/), и как нестрогая дизъюнкция (?), поэтому ему отвечает также схема: a ú b ú c ú d; Понятие опровержения Опровержение - логическая операция установления ложности или необоснованности ранее выдвинутого тезиса. Опровержение должно показать, что: 1) неправильно построено само доказательство (аргументы или демонстрация); 2) выдвинутый тезис ложен или не доказан. Суждение, которое надо опровергнуть, называется тезисом опровержения. Суждения, с помощью которых опровергается тезис, называются аргументами опровержения, Существуют три способа опровержения: I) опровержение тезиса (прямое и косвенное); II) критика аргументов; III) выявление несостоятельности демонстрации.
|
||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.13.192 (0.006 с.) |

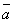 ) будет антитезисом, т.е. противоречащим тезису суждением.
) будет антитезисом, т.е. противоречащим тезису суждением. , при этом
, при этом 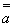 , которое по закону двузначной классической логики (
, которое по закону двузначной классической логики ( b
b 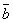 ^
^  ^
^ 



