
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Специфика закона непротиворечия в неклассических логикахСодержание книги
Поиск на нашем сайте В результате исследования 9 формализованных логических систем выявлено, что из 12 приведенных видов отрицания для 7 видов закон непротиворечия является тавтологией (или доказуемой формулой), для остальных же 5 закон непротиворечия тавтологией (доказуемой формулой) не является. По сравнению с законом исключенного третьего закон непротиворечия более устойчив. Закон непротиворечия не является тавтологией во многих многозначных логиках. В классической, интуиционистской и конструктивных логиках закон непротиворечия, наоборот, признается неограниченно действующим. Причина в том, что в многозначных логиках число значений истинности может быть как конечным (большим 2), так и бесконечным. В логических системах, в которых отражена жесткая ситуация, “или - или” (истина - ложь), закон непротиворечия и закон исключенного третьего -тавтологии. Но это предельные случаи в познании (истина или ложь). Если же в процессе познания мы еще не достигли истины или еще не опровергли какое-либо утверждение (доказав его ложность), то нам приходится оперировать не истинными или ложными, а неопределенными суждениями. Классическая двузначная логика должна быть дополнена многозначными логиками, в частности бесконечнозначной логикой, которая применима в процессе рассуждения об объектах, отражаемых в понятиях с нефиксированным объемом, и бесконечное число значений истинности которой лежит в интервале от 1 до 0. Совсем другие ситуации в познании отражены в конструктивных и интуиционистской логиках: конструктивный процесс или имеется (осуществляется), или его нет, но то и другое не может иметь места одновременно по отношению к одному и тому же конструктивному объекту или процессу, поэтому закон непротиворечия в этих логиках действует неограниченно. В конструктивных логиках приняты абстракции, отличные от тех, которые приняты в многозначных логиках. В конструктивных и интуиционистской логиках принимаются лишь два знамения истинности - истина и ложь, доказуемо (выводимо) или недоказуемо (невыводимо), поэтому закон непротиворечия - выводимая формула. Однако независимо от того, является ли закон непротиворечия в той или иной логической системе тавтологией или не является, сами логические системы строятся непротиворечиво: иными словами, метатеория (металогика) построения формализованных систем подчиняется закону непротиворечия, иначе такие системы были бы бесполезными, так как в них было бы выводимо все что угодно - как истина, так и ложь. Очень важным в гносеологическом и логическом плане результатом является то, что закон непротиворечия и закон исключенного третьего нельзя опровергнуть, так как отрицание этих законов ни в одной из известных форм, ни в одной из исследованных автором 18 логических системах не является тавтологией (или выводимой, доказуемой формулой), что свидетельствует об их фундаментальной роли в познании. Закон непротиворечия - один из основных законов правильного человеческого мышления - устойчив, его нельзя опровергнуть и заменить другим, в противном случае стерлось бы различие в познании между истиной как его целью и ложью. Многообразие логических систем свидетельствует о развитии науки логики в целом и ее составных частей, в том числе теории основных фундаментальных формально-логических законов - закона непротиворечия и закона исключенного третьего. Модальные логики В классической двузначной логике рассматривались простые и сложные ассерторические суждения, т. е. такие, в которых не установлен характер связи между субъектом и предикатом, например: “Морская вода соленая” или “Дождь то начинал хлестать теплыми крупными каплями, то переставал”. В модальных суждениях раскрывается характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном модальном суждении. Например: “Необходимо, что металлы - проводники электрического тока” или “Если будет дуть попутный ветер, то, возможно, мы приплывем в гавань до наступления темноты”. Модальными являются суждения, которые включают модальные операторы (модальные понятия), т. е. слова “необходимо”, “возможно”, “невозможно”, “случайно”, “запрещено”, “хорошо” и многие другие (см. главу III, § 6 “Деление суждений по модальности”). Модальные суждения рассматриваются в специальном направлении современной формальной логики - в модальной логике. Изучение модальных суждений имеет длительную и многогранную историю. Мы отметим лишь некоторые из ее аспектов. Модальности в логику были введены Аристотелем. Термин “возможность”, по Аристотелю, имеет различный смысл. Возможным он называет и то, что необходимо, и то, что не необходимо, и то, что возможно. Исходя из понимания модальности “возможность”, Аристотель писал о неприменимости закона исключенного третьего к будущим единичным событиям. Наряду с категорическим силлогизмом Аристотель исследует и модальный силлогизм, у которого одна или обе посылки и заключение являются модальными суждениями. Я. Лукасевич в книге “Аристотелевская силлогистика с точки зрения современной формальной логики” две главы посвящает аристотелевской модальной логике предложений (гл. VI) и модальной силлогистике Аристотеля (гл. VIII)'. Аристотель рассматривает модальную силлогистику по образцу своей ассерторической силлогистики: силлогизмы подразделяются на фигуры и модусы, неправильные модусы отбрасываются с помощью их интерпретации на конкретных терминах. Согласно Аристотелю, случайность есть то, что не необходимо и не невозможно, т. е. р - случайно означает то же самое, что и р - не необходимо и р - не невозможно, но Лукасевич отмечает, что аристотелевская теория случайных силлогизмов полна серьезных ошибок2. Итог исследований Лукасевича такой: пропозициональная модальная логика Аристотеля имеет огромное значение для философии; в работах Аристотеля можно найти все элементы, необходимые для построения полной системы модальной логики; однако Аристотель исходил из двузначной логики', в то время как модальная логика не может быть двузначной. К идее многозначной логики Аристотель подошел вплотную, рассуждая о “будущем мореном сражении”. Следуя Аристотелю, Лукасевич в 1920 г. построил первую многозначную (трехзначную) логику. Так осуществляется связь модальных и многозначных логик. Значительное внимание разработке модальных категорий уделяли философы в Древней Греции и особенно Диодор Крон, рассматривавший модальности в связи с введенной им временнбй переменной. В средние века модальным категориям также уделялось большое внимание. В XIX в. категорию вероятности разрабатывали Дж. Буль и П. С. Порецкий. Возникновение модальной логики как системы датируется 1918г., когда американский логик и философ Кларенс Ирвинг Льюис (1883-1964) в работе “A Survey of Symbolic Logic” сформулировал модальное исчисление, названное им впоследствии S3. В книге “Simbolic Logik”, написанной им совместно с К. Лэнгфордом в 1932 г., он сформулировал еще пять модальных логических систем, связанных с S3 и между собой. Это - системы S1, S2, S4, S5,S6. Приведем описание модальной системы S12. I. Исходные символы: 1. р, q, r и т. д. - пропозициональные переменные; 2. ~ р - отрицание р 3. р* q – конъюнкция p и q; 4. р 5. () р- модальный оператор возможности (возможно p); 6. р = q - строгая эквивалентность, р = q равносильно (р II. Аксиомы системы S1: 1) p*q 2) p*q 3) p 4) (p*q)*r 5) р 6)(p 7) p*(p Аксиома 5 может быть выведена из остальных, как было показано позднее. Так как конъюнкция связывает “сильнее”, чем импликация, то скобки можно опустить или заменить их точками; как это сделано у Льюиса. III. Правила вывода S1: 1) Правило подстановки. Любые два эквивалентных друг другу выражения взаимозаменимы. 2) Любая правильно построенная формула может быть подставлена вместо р, или q. или r и т. д. в любом выражении. 3) Если выводим о р и выводим о q, то выводимо р • q. 4) Если выводим о р и выводим о р
Льюис построил модальную пропозициональную логику S1 в виде расширения немодального (ассерторического) пропозиционального исчисления. При этом основные черты S1и других его исчислений были скопированы с формализованной логической системы Principia Mathematica Рассела и Уайтхеда, сформулированы с помощью понятий, только терминологически отличающихся от понятий, использованных в Principia Mathematica. Кроме Рассела и Уайтхеда, идеи классической логики развивали многие современные математические логики, например, американский логик и математик С. Клини'. Исчисления Льюиса построены аксиоматически по образцу Principia, и по аналогии с Principia Льюис доказывает ряд специфических теорем. В классической двузначной логике логическое следование отождествляется с материальной импликацией и допускаются такие формы вывода: p→ (q→p). (1) т. е. истинное суждение следует из любого суждения (“истина следует откуда угодно”), p→(
т. е. из ложного суждения следует любое суждение (“из лжи следует все, что угодно”). Это противоречит нашему содержательному, практическому пониманию логического следования, поэтому данные формулы, как и некоторые другие, и соответствующие им принципы логического следования называются парадоксами материальной импликации. Льюис создал свои новые системы с целью избежать этих парадоксов и ввести новую импликацию, названную им “строгой импликацией”, такую, чтобы логическое следование представлялось не чисто формально, а по смыслу (содержательно) и новая импликация была ближе к связке естественного языка “если, то”. В строгой импликации Льюиса р В системах Льюиса были устранены парадоксы материальной импликации, т.е. формулы (1) и (2) стали невыводимыми, но появились парадоксы строгой импликации. К ним относятся, например, такие формулы: (~ () ~ p) (~ () p) Итак, отождествлять строгую импликацию Льюиса со следованием нельзя. С целью исключить парадоксы строгой импликации Льюиса немецкий математик и логик Ф. В. Аккерман (1896 -1962) построил свою систему модальной логики. Он ввел так называемую сильную импликацию, которая не тождественна строгой импликации Льюиса, и модальные операторы Аккермана и Льюиса также не являются тождественными. Аккерман все логические термины и модальные операторы определяет через сильную импликацию так: NA равносильно Системы Льюиса и Аккермана являются бесконечнозначными. В отличие от этих систем первоначально построенные системы Лукасевича являются конечнозначными: одна - трехзначная (1920), другая - четырехзначная (1953). В четырехзначной системе Лукасевича1 также обнаружены парадоксы. Главный из них состоит в том, что ни одно аподиктическое предложение не истинно, т. е. ни одно суждение вида L Интерпретации модальных логик различны. Известный австрийский философ и логик Р. Карнап (1891-1970) пытался интерпретировать модальные понятия (операторы) с помощью так называемой теории “возможных миров”, в которой допускается наличие множества “миров”, один из которых -действительный, реальный мир, а остальные - возможные миры. Необходимым объявляется то, что существует во всех мирах, возможным - то, что существует хотя бы в одном. Р. Карнап в 1946 г., используя понятие “описание состояния”, предложил интерпретацию модальных операторов, в основе которой лежала идея различия возможного и действительного мира. В ином направлении шел финский логик Я. Хинтикка. Критически переосмыслив введенное Карнапом понятие “описание состояния”, он разработал технику “модальных множеств”, т. е. миров (1957), - оригинальную семантическую концепцию возможных миров. Разработка семантики возможных миров для модальных логик продолжается. Разнообразными проблемами модальной логики занимается американский логик Р. Фейс'. В настоящее время разработаны многие виды модальностей, которые отражены в таблице, помещенной на с. 97 данного учебника. Теорией модальных логик и построением новых модальных логических систем активно занимаются логики А. А. Ивин, Я. А. Слинин, Б. С. Чендов,0. Ф. Серебряников, В. Т. Павлов и др.
Положительные логики Положительные логики (сокращенно - ПЛ) - это логики, построенные без операции отрицания. Их можно разделить на два вида: 1) ПЛ в широком смысле слова, или квазипозитивные логики. Они построены без операции отрицания, но отрицание может быть выражено средствами их логических систем; 2) ПЛ в узком смысле слова. Они построены без операции отрицания, и отрицание не может быть выражено в их системах. Можно предложить классификацию ПЛ и по другому основанию: числу логических операций, на котором построена ПЛ. Квазипозитивными логиками, построенными на одной операции, являются логика, построенная на операции “штрих Шеффера” (антиконъюнкция), и логика, основанная на операции антидизъюнкции. Квазипозитивная логика, построенная на операции антидизъюнкции, которая соответствует сложному союзу “ни..., ни...” и обозначается а
Ряд квазипозитивных логик основан на двух операциях. ПЛ в узком смысле, основанными на одной операции, являются импликативная логика, основанная на операции импликации, и логика, построенная на операции эквиваленции. Ряд ПЛ основан на двух операциях: а) на импликации и конъюнкции; б) на дизъюнкции и конъюнкции; в) на импликации и дизъюнкции. ПЛ (в узком смысле) является подсистемой (частичной системой) более сильных логик - интуиционистской и классической. Все утверждения ПЛ имеют силу как в интуиционистской логике, так и в классической логике. Внутри самих ПЛ также имеются различные по силе системы. Так, импликативная логика, включающая две аксиомы, слабее, чем ПЛ, включающая, кроме этих двух, аксиомы, характеризующие конъюнкцию и дизъюнкцию. Аксиоматическое построение подтверждает это соотношение: самой сильной является классическая логика, слабее интуиционистская, еще слабее ПЛ. Общим для ПЛ в широком и узком смыслах является то, что среди логических констант этих систем нет операции отрицания. Отличия этих систем следующие: 1) в квазипозитивных логиках операция отрицания выразима средствами этой логики, а в ПЛ в узком смысле операция отрицания не выразима; 2) квазипозитивные логики являются моделями классической логики, т.е. они эквивалентны классической логике высказываний, а ПЛ в узком смысле не эквиваленты классической логике, являясь ее подсистемами (частичными системами), следовательно, они слабее классической логики высказываний. Роль ПЛ в искусственных языках весьма значительна. Особенно это касается конструктивной логики А. А. Маркова, которая строится на иерархии языков. В алфавите языка Я1, нет отрицания, и в нем нельзя выразить отрицание, ибо нет импликации. Марковым был построен язык Я1, который хотя и узок, но приспособлен для описания работы нормальных алгоритмов. Этот язык пригоден для выражения некоторых отношений между словами, встречающимися в чистой семиотике и в теории алгоритмов. С помощью языка Я1, (языка без отрицания) можно дать описание работы различных алгоритмов - и в этом состоит важное значение языка без операции отрицания. Логическая система без операции логического отрицания находит свое применение при построении машинных программ. Но если взять искусственные языки - такие, как ФОРТРАН или КОБОЛ, которые позволяют воспользоваться высокоэффективным способом программирования, то в их состав, кроме логического сложения и логического умножения, входит и логическое отрицание, соответствующее частице “не” и обозначаемое знаком “ u ”. Все инструкции о том, как произвести сборку замков, мебели, по использованию машин, инструментов, технических приборов и т. п. основаны на содержательном (не формализованном) использовании ПЛ.
Паранепротиворечивая логика Эта логика представляет одно из направлений современной неклассической математической логики. Объективной основой появления паранепротиворечивых логик является стремление отразить средствами логики специфику мышления человека о переходных состояниях, которые наряду с устойчивостью и относительным покоем наблюдаются в природе, обществе и познании. В природе и обществе происходят изменения, предметы и их свойства переходят в свою противоположность, поэтому нередки переходные состояния, промежуточные ситуации, неопределенность в познании, переход от незнания или неполного знания к более полному и точному. Действие законов двузначной логики - закона исключенного третьего и закона непротиворечия - в этих ситуациях ограничено или вообще исключено. На необщезначимость этих законов указывал еще Аристотель. Говоря о будущих единичных случайных событиях, по Аристотелю, нельзя считать суждение истинным или ложным, оно неопределенно. Закон непротиворечия утверждает, что два противоположных суждения не могут быть истинными в одно и то же время и в одном и том же отношении. Но в разное время они могут быть оба истинными. Аристотель писал: “Все изменяющееся необходимо должно быть делимым... необходимо, чтобы часть изменяющегося предмета находилась в одном (состоянии), часть - в другом, так как невозможно сразу быть в обоих или ни в одном”'. Вследствие неопределенности интервалов и неопределенности состояний изменяющегося предмета предполагается временная интервальная Паранепротиворечивая семантика, допускающая истинность как высказывания А, так и не-А. Кроме временных интервалов с переходными состояниями, наше мышление имеет дело с так называемыми нечеткими понятиями (нежесткими, расплывчатыми, размытыми –fuzzy), отражающими нежесткие множества, концепция которых предложена в 1965 г. американским математиком Л. Заде2. Все это обусловило необходимость и возможность появления паранепротиворечивых логик (paraconsistent logics) -логических исчислений, которые могут лежать в основе противоречивых формальных теорий. Противоречивые данные возникают на судебных заседаниях, в дискуссиях, полемике, при постановке диагноза болезни, в научных теориях (прежних и новых), в ситуациях, связанных с решением нравственных проблем, в других сферах интеллектуальной деятельности. В связи с этим встала проблема создания информационной системы, работающей с противоречивыми данными. Предшественниками паранепротиворечивой логики как нового вида неклассичесиой формальной логики явились логики Н. А. Васильева и Я. Лукасевича. Как новый вид математической логики паранепротиворечивая логика разрабатывалась в работах польского логика Ст. Яськовского (1948) и бразильского математика Ньютона да Коста (начиная с 1958 г.) История паранепротиворечивой логики изложена бразильским логиком А. И. Аррудой в работе “Обзор паранепротиворечивой логики. Математическая логика в Латинской Америке”'. В паранепротиворечивых системах принцип (закон) непротиворечия лишен всеобщей значимости. Логике не присущи ни единство, ни абсолютность - эту мысль мы встречаем у многих современных логиков, в том числе у Н. да Косты. В статье, написанной специально для журнала “Философские науки”, “Философское значение паранепротиворечивой логики” Н. да Коста пишет: “Допустим, что имеющийся у нас язык дедуктивной теории Т содержит в себе символ отрицания. Т называют противоречивой (inconsistent) теорией, если и только если в Т имеются две теоремы, одна из которых есть отрицание другой; в противоположном случае Т считается непротиворечивой (consistent). Т считают тривиальной, если и только если все формулы (или все высказывания [sentences]) языка Т являются также теоремами Т; в противном случае мы называем Т нетривиальной... Система логики паранепротиворечива, если она может быть использована как логика, лежащая в основе противоречивых, но нетривиальных теорий”2. Н. да Коста полагает, что вместо стандартных теорий множеств могут быть использованы паранепротиворечивые теории множеств. Система паранепротиворечивой логики в общем случае должна удовлетворять следующим условиям: 1) из двух противоречащих формул А и u А в общем случае нельзя вывести произвольную формулу В; 2) дедуктивные средства классической логики должны быть максимально сохранены, поскольку они - основа всех обычных рассуждений. В первую очередь должен быть сохранен modus poaens, т. е. рассуждение по формуле ((а > b)^ а) > b. Паранепротиворечивая логика связана со многими видами неклассических логик: с модальной логикой (системой S5 К. И. Льюиса), с многозначными логиками, с релевантной логикой, где тоже не принимается принцип: из противоречия следует все, что угодно'. Исследование многозначных логик показало, что закон непротиворечия, т. е. формула Интересны и оригинальны статьи американского математика Н. Белнапа “Как нужно рассуждать компьютеру” (1976) и “Об одной полезной четырехзначной логике” (1976), посвященные формализации общения с информационными системами, в которых содержится противоречивая информация. Белнап построил четырехзначную логику, значениями истинности которой являются следующие: Т - “говорит только Истину”; F - “говорит только Ложь”; None - “Не говорит ни Истины, ни Лжи”; Both -“говорит и Истину, и Ложь”'. Н. Белнап отмечает, что входные данные поступают в компьютер из нескольких независимых источников, и в таких условиях проявляется типичная особенность информационной ситуации - угроза противоречивости информации. Что в таком случае должен делать компьютер, особенно если в системе содержится необнаруженное противоречие? Свою четырехзначную логику Белнап и предлагает в качестве практического руководства в рассуждениях2. Итак, паранепротиворечивые логики демонстрируют возможность наличия очень сильных противоречивых, но нетривиальных (т. е. паранепротиворечивых) теорий.
Заключение Цель познания в науке и повседневной жизни - получение истинных знаний и полноценное использование их на практике. Знание формальной логики и диалектики помогает предвидеть события и лучшим способом планировать деятельность, максимально предусматривать возможные последствия, выдвигать различные гипотезы, эффективнее обучать и самим обучаться, видеть “логику вещей”, т. е. объективную диалектику, умело вести дискуссии и полемику. Изучение логики желательно продолжить, прослушав ряд спецкурсов, самостоятельно изучив дополнительную литературу. Эти формы работы помогут студентам, изучившим основной курс формальной логики (как классической, так и многочисленных направлений неклассических логик, изложенных в последней главе), стать преподавателем логики в средней школе, лицее, гимназии и ином учебном заведении. Можно предвидеть, что потребность в таких преподавателях будет возрастать в связи с введением курса логики в средних учебных заведениях. В статье доктора философских наук В. А. Светлова “Нужна ли логика будущему учителю?” (вопрос, вынесенный в заголовок, носит в общем риторический характер) сформулированы некоторые перспективы дальнейшего изучения логики студентами педвузов. В. А. Светлов пишет: “Что же может дать логика для подготовки учителя? При самом умеренном ее изучении студент педагогического вуза за один-два семестра мог бы дополнительно к стандартному курсу освоить теоретически и научиться применять практически (по выбору): логику научного исследования, логические основы семантики и семиотики, логику научно-педагогической работы, логику принятия решения (в условиях определенности, неопределенности и риска), логику спора, логику общения (межличностных отношений), логику структурного анализа сказок, мифов, художественных текстов, логику конфликтов (межличностных, политических, военных)”'. Помимо этих направлений будущим преподавателям логики можно посоветовать изучить материалы по методике преподавания логики и по истории логики. Интересным, перспективным направлением является анализ уже созданных и разработка новых программ для ЭВМ по курсу формальной логики - как традиционной (с элементами символической логики), так и символической логики2. Широкое применение логических знаний необходимо и при разработке обучающих программ для ЭВМ по различным школьным учебным дисциплинам (опыт составления разнообразных программ по математике, русскому языку, истории, иностранным языкам, географии и другим предметам имеется, и его предстоит изучить). Конкретное применение знаний формальной логики учителю потребуется и в вузе, и в школе при работе с понятиями и осуществлении логических операций с ними (определение, деление понятий, классификация, обобщение и ограничение). Знание темы “Суждение” поможет учителю и учащимся четко выявлять логическую структуру простых и сложных суждений, правильно производить отрицания суждений, работать с модальными суждениями. Мы надеемся, что запись сложных суждений с помощью логических союзов, которая очень нравится учащимся 3-7 и старших классов (о чем свидетельствуют многочисленные эксперименты со школьниками, изучавшими элементы логики под моим и под руководством студентов МПГУ им В. И. Ленина) оживит урок по любому школьному предмету. Тема “Умозаключение” и ее использование отражены в данной книге подробно; в ней выделены два отдельных параграфа: “Дедукция и индукция в учебном процессе” и “Умозаключение по аналогии и его виды”. Желательно в процессе преподавания любого предмета показать структуру многих форм умозаключений, при этом предложить учащимся поискать в художественной литературе примеры на эти виды умозаключений. Например, в рассказе Агаты Кристи “Двойная улика” месье Пуаро расследует похищение ряда драгоценностей из коллекции Хардмана (жемчужины, рубины, изумрудное ожерелье). Подозрение могло касаться четверых. Вот их диалог, в котором сформулировано умозаключение: “- Мистер Хардман, кого Вы сами подозреваете из этой четверки? - О, месье Пуаро, что за вопрос! Ведь я Вам уже сказал, что это мои друзья. Я ни одного из них не подозреваю или, если Вам угодно, - всех в одинаковой мере. - Не могу с Вами согласиться. Я уверен, что Вы кого-то из них подозреваете. Это не графиня Росакова. Это не мистер Паркер. Кто же тогда: леди Ранкорн или мистер Джонстон?”'. Структура этого умозаключения такая: (a Это относительно новая разновидность структуры разделительно-категорического умозаключения. Вообще в художественной литературе можно найти богатейшее собрание самых интересных иллюстраций по курсу логики; следует к такой работе подключить и студентов, и учащихся школы. Это одна из заманчивых перспектив в методике изучения логики, свидетельствующая о тесном взаимодействии языка и мышления. Значительный интерес представляет раздел логики, посвященный спору, дискуссиям, разоблачению различных недопустимых уловок, используемых в полемике. В исследование этой темы оригинальный вклад внес русский логик С. И. Поварнин (1870-1952)2. После изучения курса логики рекомендуем проверить свои знания. Для этого можно ответить на предлагаемые ниже задания тестов.
Рекомендуемая литература I. Учебная литература Гетманова А. Д. Логика. М., 1986. Гетманова А. Д. Учебник по логике. Серия: Российский лицей. М.., 1994. Гетманова Л. Д., Панов М. И., Уемов А. И., Никифоров А. Л., Яшин Б. Л. Логика: Учебное пособие для учащихся 10-11 классов. М., 1995. Горский Д. П. Логика. М., 1963. Горский Д. П., Ивин А. А., Никифоров А. Л., Краткий словарь по логике. М., 1991. Ивлев Ю. В. Логика. М., 1997. Кириллов В. И., Старченко А. А. Логика. М., 1995. Мельников А.Н. Сборник задач по логике. Киев, 1990. Пойа Д. Математика и правдоподобные рассуждения. М., 1975. Сборник упражнений по логике. Минск, 1995. Светлое В. А. Практическая логика. С.-Петербург. 1995. Свинцов В. И. Логика. М., 1987. Теория и практика полемики: Методическое пособие. Томск, 1989. Уемов А. И. Основы практической логики. Одесса. 1997. Упражнения по логике. М., 1990. Яшин Б. Л. Сборник задач и упражнений по логике. М., 1996. II. Популярная литература Айзенк Г. Ю. Проверьте свои интеллектуальные способности //Пер. с англ. Рига, 1992. Гарднер М. А. А ну-ка, догадайся! // Пер. с англ. М., 1984. Жоль К. К. Логика в лицах и символах: Научно- популярная книга. М., 1993. Ивин А. А. Искусство правильно мыслить: Книга для учащихся. М., 1990. Ивин А. А. Строгий мир логики. Серия: Библиотека детской энциклопедии “Ученые - школьнику”. М., 1988. Игры для интенсивного обучения. М., 1991. КасабуцкийН. И., Скобелев Г. Н. и др. Давайте поиграем. М., 1991. Кэрролл Л. История с узелками. М., 1973. Кэрролл Л. Приключения Алисы в Стране Чудес. Сквозь Зеркало и что там увидела Алиса, или Алиса в Зазеркалье. М., 1979, Кэрролл Л. Логическая игра. М., 1991. Месъков В. С., Карпинская О. Ю. и др. Логика: Наука и искусство. М.,1993. Нагибин Ф. Ф., Канин Ё. С. Математическая шкатулка: Пособие для учащихся. М., 1984. Никольская И. Л., Семенов Е. Е. Учимся рассуждать и доказывать: Книга для учащихся 6-10 классов средней школы. М., 1989. Петров Ю. А. Азбука логичного мышления. М., 1991. Смаллиан Р. Как же называется эта книга? М., 1981. Смаллиан Р. Принцесса или тигр? М., 1985. Смаллиан Р. Алиса в Стране Смекалки. М., 1987. Сопер П. Основы искусства речи // Пер. с англ. М., 1992. Развивающие игры для детей: Справочник. М., 1990. III. Литература по педагогическим приложениям логики Богданова О. Ю. Развитие мышления старшеклассников на Уроках литературы. М., 1979. Бирюков Б. В. Жар холодных чисел и пафос бесстрастной логики. Формализация мышления от античных времен до эпохи кибернетики. М., 1985. Дзыбенко О. Г. Вопросы формирования дискуссионной речи. Тернополь, 1992. Гнеденко Б. В. Формирование мировоззрения учащихся в процессе обучения математике. М., 1982. Кирюшкин В. А. Логические упражнения в первом классе в системе занятий по русскому языку//Ученые записки Красноярского пединститута. Красноярск, 1961. Т. 19. Конобеевский Н. П., Кирюшкин В. А. Методическое руководство к альбому рисунков для логических упражнений на уроках русского языка во II классе. М., 1970. Лернер И. Я. Развитие мышления учащихся в процессе обучения истории. М., 1982. Соболевский Р. Ф. Логические и математические игры. Минск, 1977. Сухомлинский В. А. О воспитании. М., 1975. Тигранова Л. И. Развитие логического мышления детей с недостатками слуха. М., 1991. Усова А. Ф. Формирование у школьников научных понятий в процессе обучения. М., 1986. Ушинский К. Д. Первые уроки логики // Собр. соч. М.- Л., 1948. Т. 4. С. 554-578.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.013 с.) |

 q - строгая импликация льюисовской системы;
q - строгая импликация льюисовской системы; →q) (2)
→q) (2) →?, МА равносильно
→?, МА равносильно  . Здесь А - любая правильно построенная формула системы Аккермана; N- оператор необходимости; М- оператор возможности;
. Здесь А - любая правильно построенная формула системы Аккермана; N- оператор необходимости; М- оператор возможности;  - логическая постоянная, обозначающая “абсурдно”. Эта постоянная в свою очередь определяется так: А&
- логическая постоянная, обозначающая “абсурдно”. Эта постоянная в свою очередь определяется так: А&  , где & обозначает конъюнкцию. И последняя формула читается так: из противоречия, т. е. А и не-А, следует абсурд. В системе Аккермана не выводятся формулы, структурно подобные парадоксам материальной или строгой импликации.
, где & обозначает конъюнкцию. И последняя формула читается так: из противоречия, т. е. А и не-А, следует абсурд. В системе Аккермана не выводятся формулы, структурно подобные парадоксам материальной или строгой импликации.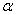 (где L обозначает необходимость, а
(где L обозначает необходимость, а  b (“ни а, ни b), таблично определена так:
b (“ни а, ни b), таблично определена так: , не является тавтологией в следующих системах: трехзначных логиках - Я. Лукасевича, Г. Рейхенбаха (для циклического и диаметрального отрицаний), Р. П. Гудстейна, Д. Бочвара (для внутреннего отрицания); т -значной логике Э. Л. Поста. Автор этого учебника исследовала 13 формализованных логических систем с 17 имеющимися в них видами отрицания и установила, что для 10 видов закон непротиворечия является тавтологией (доказуемой формулой), а для остальных 7 нет. Это обусловлено тем, что, кроме значений истинности - “истина” и “ложь”, в многозначных логиках имеется значение “неопределенно”. Но в классической, конструктивных и интуиционистской логиках от закона непротиворечия нельзя отказаться, ибо в этих логиках отражены жесткие ситуации “или - или” (“истина - ложь”), конструктивный процесс присутствует или его нет, одновременно того и другого не бывает. Поэтому классическая, интуиционистская, конструктивная и ряд других логик не годятся в качестве логик, которые могут быть основанием противоречивых, но нетривиальных теорий. Положительные логики также для этого не годятся, ибо в них нет операции отрицания. Некоторое современные логики (например, немецкий логик К. Вессель) не признают паранепротиворечивых логик. Построением паранепротиворечивых логических систем занимаются, однако, отечественные логики А. С. Карпенко, А. Т. Ишмурагов и др.
, не является тавтологией в следующих системах: трехзначных логиках - Я. Лукасевича, Г. Рейхенбаха (для циклического и диаметрального отрицаний), Р. П. Гудстейна, Д. Бочвара (для внутреннего отрицания); т -значной логике Э. Л. Поста. Автор этого учебника исследовала 13 формализованных логических систем с 17 имеющимися в них видами отрицания и установила, что для 10 видов закон непротиворечия является тавтологией (доказуемой формулой), а для остальных 7 нет. Это обусловлено тем, что, кроме значений истинности - “истина” и “ложь”, в многозначных логиках имеется значение “неопределенно”. Но в классической, конструктивных и интуиционистской логиках от закона непротиворечия нельзя отказаться, ибо в этих логиках отражены жесткие ситуации “или - или” (“истина - ложь”), конструктивный процесс присутствует или его нет, одновременно того и другого не бывает. Поэтому классическая, интуиционистская, конструктивная и ряд других логик не годятся в качестве логик, которые могут быть основанием противоречивых, но нетривиальных теорий. Положительные логики также для этого не годятся, ибо в них нет операции отрицания. Некоторое современные логики (например, немецкий логик К. Вессель) не признают паранепротиворечивых логик. Построением паранепротиворечивых логических систем занимаются, однако, отечественные логики А. С. Карпенко, А. Т. Ишмурагов и др. b
b 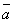
 ):(с
):(с 


