Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложное суждение и его виды.Содержание книги
Поиск на нашем сайте
Исчисление высказываний Сложные суждения образуются из простых суждений с помощью логических связок: конъюнкции, дизъюнкции, импликации, эквиваленции и отрицания. Таблицы истинности этих логических связок следующие:
Буквы а, b - переменные, обозначающие суждения; буква “И” обозначает истину, а “Л” - ложь. Таблицу истинности для конъюнкции (а U b) можно разъяснить на следующем примере. Учителю дали короткую характеристику, состоящую из двух простых суждений: “Он является хорошим педагогом (а) и учится заочно (b)”. Она будет истинна в том и только в том случае, если суждения а и b оба истинны. Это и отражено в первой строке. Если же о ложно, или b ложно, или и а, и b ложны, то вся конъюнкция обращается в ложь, т. е. учителю была дана ложная характеристика. Суждение “Увеличение рентабельности достигается или путем повышения производительности труда (а), или путем снижени себестоимости продукции (b)” - пример нестрогой дизъюнкции. Дизъюнкция называется нестрогой, если члены дизъюнкции не исключают друг друга. Высказывание или формула с такой дизъюнкцией истинна в том случае, когда истинно хотя бы одно из двух суждений (первые три строки таблицы), и ложна, когда оба суждения ложны. Строгая дизъюнкция (а u b) - та, в которой члены дизъюнкции исключают друг друга. Ее можно разъяснить на примере: “Я поеду на Юг на поезде (а) или полечу туда на самолете (b)”. Я не могу одновременно ехать на поезде и лететь на самолете. Строгая дизъюнкция истинна тогда, когда лишь одно из двух простых суждений истинно, и только одно. Таблицу для импликации (а > b) можно разъяснить на таком примере: “Если по проводнику пропустить электрический ток (а), то проводник нагреется (b)1. Импликация истинна всегда, кроме одного случая, когда первое суждение истинно, а второе - ложно. Действительно, не может быть, чтобы по проводнику пропустили электрический ток, т. е. суждение (а) было истинным, а проводник не нагрелся, т. е. чтобы суждение (b) было ложным. В таблице эквиваленция (a? b) характеризуется так: а? b истинно в тех и только в тех случаях, когда и а, и b либо оба истинны, либо оба ложны. Отрицание суждения а (т. е. a) характеризуется так: если а истинно, то его отрицание ложно, и если а - ложно, то. a - истинно. Если в формулу входят три переменные, то таблица истинности для этой формулы, включающая все возможные комбинации истинности или ложности ее переменных, будет состоять из 23 = 8 строк; при четырех переменных в таблице будет 24 = 16 строк; при пяти переменных в таблице имеем 25 = 32 строки; при n переменных 2n строк. Алгоритм распределения значений И и Л для переменных (например, для четырех переменных а, b, с, d) таков: (см. таблицу на стр. 81); Имеем 24 = 16 строк. В столбце для а сначала пишем 8 раз “И” и 8 раз “Л”. В столбце для b сначала пишем 4 раза “И” и 4 раза “Л”, затем повторяем и т. д. Тождественно-истинной формулой называется формула, которая при любых комбинациях значений для входящих в нее переменных принимает значение “истина”. Тождественно-ложная формула -та, которая (соответственно) принимает только значение “ложь”. Выполнимая формула может принимать значения как “истина”, так и “ложь”.
Так как в последней колонке имеем одни истины, то формула является тождественно-истинной, или законом логики (или, как иногда ее называют, тавтологией).
Итак, конъюнкция (а ^ b) истинна тогда, когда оба простых суждения истинны. Строгая дизъюнкция (а u b ) истинна тогда, когда только одно простое суждение истинно. Нестрогая дизъюнкция (а v b ) истинна тогда, когда хотя бы одно простое суждение истинно. Импликация (а > b ) истинна во всех случаях, кроме одного: когда а - истнно, b - ложно. Эквиваленция (а Способы отрицания суждений Два суждения называются отрицающими или противоречащими друг другу, если одно из них истинно, а другое ложно (т. е. не могут быть одновременно истинными и одновременно ложными).
1. А - О. “Все S суть Р” и “Некоторые Sне суть Р”. 2. Е -1. “Ни одно S не суть Р” и “Некоторое S суть Р”. 3. “Это S суть Р” и “Это S не суть Р”. Oперацию отрицания в виде образования нового суждения из данного следует отличать от отрицания, входящего в состав отрицательных суждений. Существует два вида отрицания: внутреннее и внешнее. Внутреннее - указывает на несоответствие предиката субъекту (связка выражена словами: “не суть”, “не есть”, “не является”). Например: “Некоторые Отрицание сложных суждении Чтобы получить отрицание сложных суждений, имеющих в своем составе лишь операции конъюнкции и дизъюнкции, необходимо поменять знаки операций друг на друга (т. е. конъюнкцию на дизъюнкцию и наоборот) и над буквами, выражающими элементарные высказывания, написать знак отрицания, а если он уже есть, то отбросить его.
Противоречащее суждение будет:
Оно читается так: “У меня будет свободное время, но я не буду вязать и не буду смотреть телевизор”. Исчисление высказываний I. Символы исчисления высказываний состоят из знаков трех категорий: 1. а, b, с,d, е,f... и те же буквы с индексами а1,а2,... Эти символы называются переменными высказываниями, или пропозициональными переменными. С помощью этих символов записываются повествовательные предложения, выражающие суждения (высказывания). 2. Символы, обозначающие логические термины:—, ^, 3. Скобки: (). Иных символов, кроме указанных, исчисление высказываний не имеет. II. Определение формулы (или правильно построенной формулы - ППФ). 1. Переменное высказывание есть формула (а, b, с...). 2. Если А и В есть ППФ, то Ничто иное не является формулой (ППФ). Так, не являются формулами: (а ^ b; а-b; ^ а; а →b; а ^ b; а Существуют правила опускания скобок. При этом исходят из того, что связка связывает сильнее, чем все остальные; связка ^ сильнее, чем →. В силу этих правил формулу (а ^ b) Однако не всякая формула может быть записана без употребления скобок. Например, в формулах а → (b → с), а ^ (b→с) исключение скобок невозможно. Для моделирования с помощью ЭВМ текстов естественного языка, включающих отрицание, возможно записать некоторые выражения на языке алгебры логики (А, В, С, D - высказывания, “+” - знак нестрогой дизъюнкции, “•” - знак конъюнкции, “-” -знак отрицания.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.254.229 (0.007 с.) |

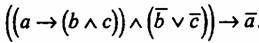
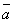
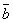


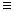 b) истинна тогда, когда оба суждения истинны или оба ложны. Отрицание (
b) истинна тогда, когда оба суждения истинны или оба ложны. Отрицание ( Отрицающим являются следующие пары суждений:
Отрицающим являются следующие пары суждений: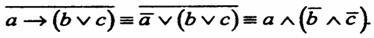 люди не имеют высшего образования”. Внешнее отрицание означает отрицание всего суждения. Например: “Неверно, что в Москве протекает река Нева”.
люди не имеют высшего образования”. Внешнее отрицание означает отрицание всего суждения. Например: “Неверно, что в Москве протекает река Нева”.
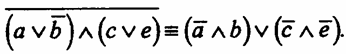

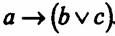
 , u, →?. Эти символы выражают следующие логические операции (логические связки): отрицание (“не”), конъюнкция (“и”), нестрогая дизъюнкция (нестрогое “или”), строгая дизъюнкция (строгое “или”), импликация (“если..., то”) эквиваленция (“если и только если, то...”). Подробнее об этих логических терминах см. на с. 26-27 этого учебника.
, u, →?. Эти символы выражают следующие логические операции (логические связки): отрицание (“не”), конъюнкция (“и”), нестрогая дизъюнкция (нестрогое “или”), строгая дизъюнкция (строгое “или”), импликация (“если..., то”) эквиваленция (“если и только если, то...”). Подробнее об этих логических терминах см. на с. 26-27 этого учебника. , (А ^ В), (А
, (А ^ В), (А