Элементы математической логики

Принципы поиска и обработки информации в ЭВМ основываются на законах математической логики, поскольку компьютеры — это автоматические устройства, принципы работы которых базируются на элементарных законах двоичной логики.

Вычислительные машины всех поколений состояли и состоят из логических элементов и элементов памяти, принимающих два значения (бита) 0 и 1. Вся обработка информации в ЭВМ всех ее логических блоков, логических схем и устройств опиралась и будет опираться на законы и принципы математической логики.

Логика — это древнейшая наука, изучающая правильность суждений, рассуждений и доказательств. Примеры суждений: «снег белый», «2 х 2 = 5», «Земля круглая», «информатика — лженаука», «Интернет — международная сеть».

Математическая логика — это математическая дисциплина, изучающая технику доказательств. Компьютеры, как и математики, требуют точности и строгости в определениях, описаниях, доказательствах и обоснованиях, чем они отличаются от обычных нормальных людей. И на них нельзя обижаться.

Отличие вычислительных операций и математических суждений от обычных человеческих действий и высказываний состоит в следующем. Вычислительные операции и математические суждения всегда предполагают однозначную интерпретацию, в то время как действия и высказывания людей зачастую допускают многозначную художественную трактовку.

Суждения и в математике, и на практике могут быть истинными или ложными. На практике истинность или ложность суждений проверяется их соответствием действительности, а в математике — опровержениями либо доказательством.

Пример истинного суждения — «снег белый». Пример ложного суждения — «генетика — лженаука». Пример суждений, истинность которых до сих пор до конца еще не установлена: «машина может думать», «на Марсе есть жизнь», «информатика — наука».

Работа ЭВМ как автоматических устройств основана исключительно на однозначных правилах выполнения команд, программ и алгоритмах обработки данных. Тем самым работа компьютеров, а также всех вычислительных устройств, систем и сетей допускает верификацию — строгую однозначную проверку правильности их работы.

Все сложные логические элементы и блоки вычислительных машин и устройств конструируются из простейших логических элементов с помощью логических операций «И» (AND), «ИЛИ» (OR) и «НЕ» (NOT). В математической логике для этих операций обычно используются обозначения — & («И»), V («ИЛИ») и — («НЕ»).

Наглядной иллюстрацией этих логических связок служат следующие диаграммы:

 

 

Отрицание не А истинно или ложно в зависимости от истинности исходного суждения А. Свойства отрицания не как логической связки можно описать таблицей истинности:

Таблица истинности:

 

 

Свойства отрицаний:

НЕ1: Отрицание ложно, если суждение истинно.

НЕ2: Отрицание истинно, если суждение ложно.

Для понимания роли отрицаний в языках запросов важно уметь выражать их в позитивной форме. Приведем примеры отрицания математических неравенств и их эквивалентные позитивные переформулировки:

не (х = 0) ≡ (х ≠ 0);

не (х ≠ 0) ≡ (х = 0);

не (х > 0) ≡ (х ≤ 0);

не (х < 0) ≡ (х ≥ 0);

не (х ≥ 0) ≡ (х < 0);

не (х ≤ 0) ≡ (х > 0).

 

Для общего понимания математических суждений, утверждений и отрицаний необходимо иметь представления обобщих законах математики и математической логики в частности. Первым среди общих законов математической логики явлется

Закон двойного отрицания:

не (не А) = А.

 

Отрицание отрицания равносильно исходному утверждению.

Логическая связка и в математической логике называется конъюнкцией. Таблица истинности конъюнкции:

 

 

Свойства конъюнкции:

И1: Конъюнкция А и В истинна, когда истинны оба суждения.

И2: Конъюнкция А и В ложна, когда ложно хотя бы одно из суждений А или В.

 

Логическая связка или в математической логике называется дизъюнкцией. Таблица истинности дизъюнкции:

 

 

Свойства дизъюнкции:

ИЛИ1: Дизъюнкция А или В истинна, когда истинно любое из суждений А или В.

ИЛИ2: Дизъюнкция А или В ложна, когда ложны оба суждения А и В.

 

Для понимания принципов поиска информации по запросам в базах данных и сети Интернет необходимо понимать математический смысл сложносоставных запросов с использованием логических операций «И» (AND), «ИЛИ» (OR) и «НЕ» (NOT).

Примеры сложносоставных запросов к базам данных и их эквивалентные позитивные переформулировки:

(признак ≠ 0) & не (х > 0) ≡ (признак (0)) & (х ≤0);

(число > 0) v не (у > 0) ≡ (число > 0) v (у ≤ 0).

Общие принципы отрицания дизъюнкций и конъюнкций в математической логике выражаются двумя закона де Моргана:

Закон отрицания конъюнкции:

не (А и В) = (не А) или (не В)

— отрицание конъюнкции суждений равносильно дизъюнкции отрицаний.

Закон отрицания дизъюнкции:

Не (А или В) ((не А) и (не В))

— отрицание дизъюнкции суждений равносильно конъюнкции отрицаний.

 

Знание и использование данных трех общих законов логики позволяют полностью избавляться от негативных формулировок в запросах к базам данных и в общении друг с другом. Но еще важнее знание этих законов для понимания принципов и результатов поиска информации компьютерами.

Попробуйте проверить законы отрицания в запросах к Интернет и объясните результаты, полученные от различных поисковых систем:

запрос: «учебник -физика» — «учебник, но не по физике?»

запрос: «учебник -книга» — «учебник, но не книга?»

запрос: «-учебник информатика» — «не учебник, но по информатике?»

запрос: «-(-учебник)» — «неверно, что это не учебник»???.

Задача 1. Проверьте закон двойного отрицания не (не А) ≡ А с помощью таблиц истинности.

 

 

Сравнение крайних столбцов показывает, что всюду, где высказывание А истинно, там же истинно и двойное отрицание не (не А). И наоборот, всюду, где ложно А, там ложно и двойное отрицание не (не А). Следовательно, двойное отрицание тождественно исходному высказыванию: не (не А) ≡ А.

Задача 2. Сравните с помощью таблиц истинности отрицание дизъюнкции и отрицание конъюнкции не (А и В) и не (А или В).

 

Решение.

 

Вопросы

 

1. Что такое дизъюнкция?

2. Что такое конъюнкция?

3. Когда истинно отрицание?

4. Когда ложно отрицание?

5. Когда истинна конъюнкция?

6. Когда истинна дизъюнкция?

7. Чему соответствует отрицание отрицания?

8. Чему соответствует отрицание конъюнкции?

9. Чему соответствует отрицание дизъюнкции?

 

Задания

 

1. Проверьте запросы с отрицаниями в Интернет и объясните полученные результаты:

запрос: «-(-интернет)»

запрос: «поиск -интернет»

запрос: «поиск информации -интернет»

запрос: «информатика -Ершов»

2. Составьте таблицы истинности для утверждений:

а)(не А) и (не В);

б)(не А) или (не В);

в) А и (не В);

г) А или (не В).

3. Сравните с помощью таблиц истинности логические выражения:

а) не (А и В) и(не А) или (не В);

б) не (А и В) и(не А) или (не В);

в) не (А) и В и А и (не В);

г) не (А) или В и А или (не В).

 

4. Проверьте по таблицам истинности логические законы:

а) отрицание конъюнкции:

не (А и В) ≡(не А) или (не В);

б) отрицание дизъюнкции:

не (А или В)≡(не А) и (не В);

в) отрицание отрицания:

не (не А) ≡ А;

г) отрицание двойного отрицания:

не (не (не А)) ≡(не А).

 

 

Принципы логического вывода

Могут ли компьютеры думать? — одна из самых интригующих проблем информатики как науки была сформулирована английским математиком А. Тьюрингом при появлении самых первых компьютеров.

Ответ А. Тьюринга — да, если удастся создать такие диалоговые программы, которые смогут отвечать на вопросы так же, как и люди. В настоящее время такого типа диалоговые программы получили название — экспертные системы.

Создание «искусственного интеллекта» стало целью огромного потока научных работ и исследований, вылившихся в создание программ для ЭВМ, имитирующих интеллектуальную деятельность людей — игру в шахматы, шашки, решение задач и доказательство теорем.

Первые шахматные программы и первые универсальные решатели задач были созданы еще для самых первых громоздких ЭВМ. В это же время были заложены основные принципы создания систем искусственного интеллекта, основанные на логическом выводе решения самых разнообразных интеллектуальных задач.

К концу XX в. программы, которые могут играть в шахматы наравне с людьми, появились и тиражируются для персональных компьютеров, а программистам фирмы IBM удалось для своего очередного суперкомпьютера создать шахматную программу, которая смогла обыграть Г. Каспарова — чемпиона мира по шахматам.

Все программы для ЭВМ, демонстрирующие интеллектуальное поведение, созданы и работают строго в соответствии с законами и принципами математической логики. Без понимания этих законов невозможно понимание принципов работы и развития вычислительных машин вообще и исследований в области искусственного интеллекта в частности.

Фундаментом вычислительных наук является конструктивная математика, в основе которой лежит математическая логика и теория алгоритмов. Математическая логика с самого начала использовалась для описания элементов и узлов ЭВМ, а теория алгоритмов — для изучения свойств компьютерных программ.

Основными объектами в математической логике являются высказывания и предикаты. Первые изучаются в исчислении высказываний, а вторые — в исчислении предикатов.

Высказывания — это суждения, которые могут быть истиными или ложными. Исчисление высказываний изучает свойства сложно-составных суждений и не интересуется, что утверждается в этих суждениях.

Высказывания обычно обозначаются отдельными буквами или буквами с возможными индексами. Примеры простых высказываний и их обозначений:

А = «снег белый»;

В₁= «вода теплая»;

В₂ = «земля твердая».

 

С математической точки зрения высказывания — это переменные, принимающие значения «истина» («true») или «ложь» («false»). Эти два истинностных значения иногда заменяются словами «да» («yes»), «нет» («not») либо цифрами 1 и 0.

Предикаты — это суждения о некоторых переменных объектах или их свойствах. Примеры предикатов:

 

А(х) = «цвет = х»;

В(х, у) = «х < у»,

где х, у — это некоторые переменные (объекты).

Значениями переменных в предикатах могут быть числа, слова, векторы, списки, функции, процедуры, алгоритмы, программы, более точно — конструктивные объекты. Для математической логики существенно, чтобы эти объекты имели конструктивную форму и были бы строго определены.

Примеры обозначения предикатов с конкретными значениями:

 

А (красный) = «цвет = красный»;

В (рост, 180) = «рост < 180»;

В (рост, у) = «рост < у».

 

Из приведенных примеров предикатов и высказываний понятно, что семантика языков запросов в Интернет описывается законами исчисления высказываний, а семантика языков запросов к базам данных на ЭВМ — законами исчисления предикатов (с равенствами).

Истинность сложных высказываний и предикатов может исследоваться через анализ их всевозможных интерпретаций либо путем их доказательства или опровержения. Так для опровержения любого общего утверждения достаточно указать хотя бы один контрпример.

Исчерпывающий анализ сложных высказываний проводится с помощью таблиц истинности, рассмотренных в предыдущем разделе. Высказывание — общезначимо (тождественно истинно), если оно истинно при любых значениях входящих в него суждений.

Доказательство — это последовательность суждений, обосновывающих некоторое утверждение. Собственно доказательства строятся на основе некоторых правил вывода, в которых одни утверждения являются (пред)посылками, а другие — их следствиями.

На практике исходным для доказательства утверждений являются некоторые факты и аргументы. В математике доказательства опираются на аксиомы, принятые в рассматриваемой теории, истинность которых не обсуждается.

Важнейшей операцией математической логики, на которой построены основные математические исследования теорий и доказательства теорем, является импликация, имеющая обозначение А → В.

Импликация А → В — это логическое следование. Импликация А → В читается: «если А, то В», «из А следует В», «А влечет В» и т. п. Первое суждение в импликации называется посылкой, а второе — следствием.

Примеры правил логического вывода:

а) над высказываниями:

если «на улице дождь», то «на улице мокро»;

б) над предикатами:

любит (х, конфеты) → сластена (х).

Таблица истинности импликации:

 

 

Свойства импликации:

П1: «Импликация А → В ложна,

когда посылка А истинна, а следствиеВ — ложно».

П2: «Импликация А → В истинна,

когда истинно следствие либо ложны и посылка и следствие».

 

Общий закон логического вывода был указан Аристотелем — основателем логики как научной дисциплины — и назван modus ponens:

 

 

Примеры логического вывода:

 

 

Аристотелем данная формулировка закона логического вывода была дана на языке исчисления высказываний. В таком виде она содержится во всех учебниках по логике и учебниках по математической логике.

В исчислении предикатов этот закон сохраняет свою силу. Однако в предикатной форме закон логического вывода превращается в конструктивную процедуру вывода новых сведений из имеющихся конкретных фактов и правил вывода.

Первый принцип логического вывода:

 

 

Данная процедура вывода позволяет вывести суждение В(с) из конкретного факта А(с) и правила А(х) → В(х). Пример логического вывода:

 

 

Таким образом, данное конструктивное правило позволяет выводить новые сведения из общих правил и уже известных фактов. Следовательно, знание фактических сведений и применение законов логического вывода позволяет порождать новые сведения, являющиеся их следствиями.

Этим свойством и этими законами логического вывода могут пользоваться не только люди — они применяются в механизмах автоматического доказательства теорем, заложенных в современных системах искусственного интеллекта.

Принцип вывода отрицаний — второй общий принцип логического вывода:

 

 

Данная процедура из отрицания следствия не В(с) на основании правила вывода А(х) → В(х) позволяет сделать заключение о невыполнении предпосылки не А(с). Примеры логического вывода из отрицаний:

 

 

Данный принцип также представляет конструктивную процедуру вывода новых сведений — отрицаний предросылок не А(с) при нарушении следствий не В(с) для заданного правила А(х) → В(х).

Приведенные принципы и законы логического вывода и заложены в современные модели систем искусственного интеллекта. В частности, они заложены в механизмы системы логического программирования Пролог, который в 90-х годах был принят японским правительством в основу проекта нового поколения ЭВМ.

Вопросы

 

1. Могут ли машины думать?

2. Что такое «искусственный интеллект»?

3. Что такое экспертные системы?

4. Что такое предикат?

5. Что такое импликация?

6. Когда истинна импликация?

7. В чем состоит закон логического вывода?

8. В чем заключен принцип логического вывода?

9. Как выводятся отрицания предпосылок?

Задания

 

1. Найдите в Интернет шахматную программу и попробуйте сыгрыть с ней в шахматы.

2. Найдите в шахматном программе:

а) уровень, когда Вы стабильно обыгрываете ЭВМ;

б) уровень, когда Вы играет с ЭВМ на равных.

3. Составьте таблицы истинности для утверждений:

а) А → (не В);

б) не (А → В);

в)(не А) → В;

г)(не А) → (не В).

4. Сравните с помощью таблиц истинности логические выражения:

а) А → (не В) и(не А) → В;

б) не (А → В) и(не А) → (не В).

5. Проверьте по таблицам истинности логические законы:

а) отрицание импликации:

не (А (В) ≡(не В) → (не А);

б) двойная импликация:

(А → А) ≡ А.

 

Базы знаний на ЭВМ

Основная перспектива развития механизмов поиска информации в Интернет и баз данных на ЭВМ — создание более универсальных языков запросов, все более приближающихся к обычным естественным языкам по выразительным возможностям. Эта идея лежала в основе японского проекта ЭВМ пятого поколения.

Одним из основных в японском проекте ЭВМ являлось понятие баз знаний, принятых в языке Пролог, а также экспертных систем, моделирующих поведение экспертов в некоторой предметной области знаний или профессиональной деятельности.

База знаний в ЭВМ — это совокупность фактов и правил вывода, хранящихся в памяти ЭВМ. С математической точки зрения базы знаний могут описываться в форме наборов предикатов и правил логического вывода.

Содержание баз знаний составляют конкретные и обобщенные факты и сведения об определенной предметной области или сфере деятельности. Примеры предметных областей — семья, школа, вуз, магазин, рынок, ферма, фирма, завод, офис, банк и т. п.

Любая база данных в ЭВМ может быть описана набором предикатов, описывающих имеющиеся в ней сведения. Примеры записи конкретных фактов в форме предикатов:

мама (Люба, Оля) — Люба — мама Оли

папа (Вова, Лена) — Вова — папа Лены

оценка (Вова, физика, 5) — Вова имеет 5 по физике

оценка (Лена, русский, 5) — У Лены 5 по русскому языку

любит (Лена, музыка) — Лена любит музыку

 

 

Перечисленные предикаты в языке Пролог называются фактами. Факты в Прологе — это конкретные предикаты с конкретными значениями. В качестве значений предикатов могут выступать слова, числа и словосочетания, в которых слова соединяются знаком подчеркивания.

Вопросы в языке Пролог — это запросы к базам данных и базам знаний в ЭВМ. С точки зрения математики любой вопрос на Прологе — это некоторое суждение об объектах, хранящихся в базе знаний.

Эти суждения могут быть истинными или ложными. Задача системы Пролог состоит в том, чтобы найти такие конкретные значения, которые дают положительные ответы на указанные вопросы.

 

Примеры простых вопросов на языке Пролог и ответов на них ЭВМ, в памяти которой содержится указанная выше группа фактов (предикатов):

? папа (х, Лена) — Кто папа Лены?

х = Вова

? мама (х, Лена) — Кто мама Лены?

Нет

? мама (х, у) — Кто у кого — мама?

х = Люба

у = Оля

? оценка (х, _, 5) — Кто имеет оценки 5?

х = Лена

х = Вова

 

 

Здесь буквы х, у — обозначения переменных, а числа и слова — конкретные значения аргументов в соответствующих предикатах. Знак подчеркивания «_» представляет неопределенное значение, которое несущественно для ответа на вопросы.

Запись вопросов в языке Пролог начинается со знака?, за которым записывается предикат либо группа предикатов, разделяемых запятыми. Запятая в сложносоставных вопросах на языке Пролог играет роль логической связки «И» («AND»).

 

Примеры сложносоставных вопросов на языке Пролог:

? мама (х,у), мама (у, Оля) — Кто мама у мамы Оли?

х = Зина

у = Люба

? мама (х,у), папа (у, Оля) — Кто мама у папы Оли?

НЕТ

Правила в Прологе — это правила логического вывода. Слева в правилах записывается следствие, а справа — предусловие. Предусловие может состоять из одного или нескольких предикатов, разделяемых запятыми. Примеры записи правил вывода на Прологе:

студент(х) <— занятие(х,учеба) — студент — тот, кто занят учебой;

нумизмат(х) <— собирает(х,монеты) — нумизмат — тот, кто собирает монеты.

 

Примеры вопросов на использование этих правил:

? студент(х) — Кто — студент?

х = Алеша

х = Лена

? нумизмат(у) — Кто — нумизмат?

у = Алеша

 

В правилах со сложносоставными определениями запятая также играет роль логической связки и объединяет условия, образующие определение. Такого рода правила позволяют создавать сложные базы знаний по различным предметным областям и применениям.

Базы знаний на ЭВМ могут содержать правила вывода следующих видов:

— правила определения понятий;

— правила принятия решений;

— способы решения задач;

— правила поведения и т. п.

Обобщенные сведения в базах знаний записываются в форме правил вывода, выражающих определения понятий. Примеры обобщенных сведений:

бабушка (x,z) <— мама(х,у), мама(у,z) — бабушка — это мама мамы;

двоечник(х) <— оценка(х,_,2) — двоечник — тот, у кого есть двойки.

 

Используя совокупность конкретных и обобщенных фактов и правил, компьютеры могут давать ответы на широкий круг осмысленных вопросов. Для этого соответствующая база знаний с соответствующей системой понятий и правил вывода должна храниться в памяти ЭВМ.

При определении новых понятий необходимо различать их объем и содержание. Объем понятия — это совокупность вещей или явлений, отвечающих данному понятию. Объем понятий соотносит словам и терминам соответствующие объекты предметной области.

Содержание понятия — это совокупность логических признаков, выделяющих объекты, отвечающие данному понятию, среди других объектов. С логической точки зрения определение понятия представляет описание совокупности признаков, характеризующих его содержание.

 

Приведем примеры определения понятий.

 

1. Понятие «мама». Объем понятия — совокупность всех мам. Содержание понятия — женщина, имеющая детей. Формализация понятия на Прологе может выражаться конкретными фактами. Примеры:

мама (Люба, Оля) — Люба — мама Оли;

мама (Зина, Люба) — Зина — мама Любы.

 

2. Понятие — «бабушка». Объем понятия — совокупность всех бабушек. Содержание понятия — «бабушка — это мама мамы или папы». Формализация этого понятия на Прологе:

бабушка(х,z) <- мама(х,у), мама(у,z) — бабушка — это мама мамы;

бабушка(х,z) <- мама(х,у), nana(y,z) — бабушка — это мама папы.

 

3. Понятие «музыкант». Объем понятия — совокупность людей, занимающихся музыкой. Содержание понятия — «музыкант — человек, который любит музыку и занимается музыкой». Это понятие на языке Пролог можно записать в виде правила:

музыкант (х) <- любит (х, музыка), занятие (х, музыка)

 

4. Понятие «студент». Объем и содержание понятия — учащиеся в вузах, университетах и колледжах. Определение этого понятия на Прологе можно записать в виде набора правил:

студент (х) <— занятие (х, учеба), место (х, университет);

студент (х) <— занятие (х, учеба), место (х, институт);

студент (х) <— занятие (х, учеба), место (х, колледж);

 

Для создания сложных баз знаний может понадобиться целая система понятий, характеризующих объекты в заданной предметной области. Эта система определений базируется на наборе признаков, где каждый признак является характеристикой некоторого объекта.

Вопросы

 

1. Что такое базы знаний?

2. Что такое факты на языке Пролог?

3. Что такое вопросы на языке Пролог?

4. Что такое правила на языке Пролог?

5. Что такое содержание понятия?

6. Что такое объем понятия?

Задания

 

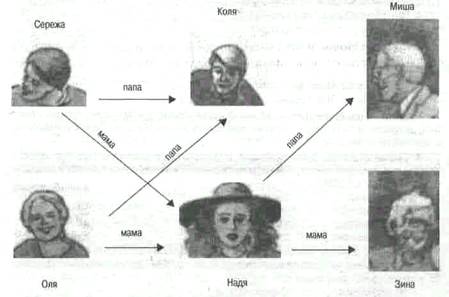
1. Найдите в Интернет интерпретатор Пролога.

2. Проверьте на ЭВМ примеры на языке Пролог.

3. Опишите на языке Пролог данные о своей семье: о маме, папе, сестрах, братьях, дедушках и бабушках - кто кому приходится мамой и папой. Подберитевопросы и проверьте их на ЭВМ.

4. Опишите данные о своих друзьях с указанием их увлечений (кто что любит), занятий (кто чем занимается). Подберите правила для определения понятий и вопросы на их проверку на ЭВМ:

а) сластена; д) спортсмен;

б) филателист; е) бизнесмен;

в) математик; ж) музыкант;

г) программист; з) мусорщик.

5. Опишите в форме фактов для себя и своих ближайших друзей-одноклассников данные об оценках по предметам и проверьте их на ЭВМ над конкретными сведения об успехах своих товарищей:

а) литература; г) физкультура;

б) математика; д) информатика;

в) физика; е) история.

6. Подберите правила определения понятий и проверьте их на ЭВМ на некоторой группе фактов:

а) математик; д) физик;

б) историк; е) лирик;

в) двоечник; ж) троечник.

г) отличник;

Законы логического вывода

Умение делать выводы — основная способность любого интеллекта. Основным признаком интеллекта являются знания и умения решать определенные задачи. Основой этих интеллектуальных умений являются законы и принципы логического вывода.

Знание законов логического вывода позволяет выверять правильность рассуждений, доказательств, а также находить ошибочные утверждения. Незнание или нарушение этих законов и принципов приводит к логическим ошибкам и принятию неправильных решений.

В качестве иллюстрации рассмотрим базу знаний о семье. Пусть в семье есть дочь Оля, сын Сережа, мама Надя, папа Коля, бабушка Зина и дедушка Миша:

 

 

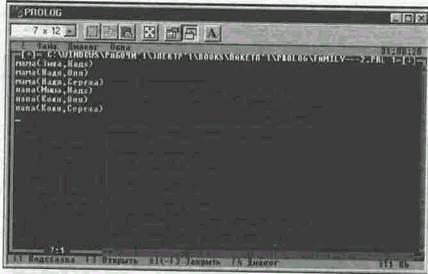
Соответствующая база данных на языке Пролог:

мама (Зина, Надя); папа (Миша, Надя);

мама (Надя, Оля); папа (Коля, Оля);

мама (Надя, Сережа); папа (Коля, Сережа);

 

 

Система Пролог при наличии этих фактов в памяти ЭВМ даст следующие ответы на вопросы о «папах» и «мамах»:

 

? мама(Надя, Оля) — Надя — мама Оли?

да

? папа(Сережа,Надя) — Сережа — папа Нади?

Нет

 

 

Машина, использующая систему Пролог, дает ответы строго в соответствии с определенными логическими законами и принципами логического вывода. Разберем эти законы и принципы.

Закон противоречия — первый общий закон логики. Этот закон впервые высказал Аристотель - основатель логики как научной дисциплины:

 

 

Примеры противоречивых утверждений:

1) «яблоко — спелое»,

«яблоко — неспелое»;

2) «треугольник ABC — прямоугольный»,

«стороны треугольника равны друг другу».

Высказывание противоречивых суждений и утверждений является примером логических ошибок. Наличие противоречий говорит о некотором умысле либо о нарушениях в сознании (базе знаний).

В системе Пролог закон противоречия используется для вывода ответов на вопросы. А именно, каждый вопрос типа? А(х) заменяется на отрицание не А(х) и присоединяется к базе знаний, хранящейся в ЭВМ.

Если получившаяся расширенная база знаний становится противоречивой, то это означает, что утверждение А(х) согласуется с исходной базой знаний и значение переменной х является ответом на заданный вопрос.

Так, вопрос? мама (Надя, Оля) ЭВМ преобразует в отрицание не мама (Надя, Оля) и временно присоединяет его к базе знаний. При этом получившаяся база становится противоречивой и система Пролог объявляет отрицание ложным и выводит ответ ДА.

Закон исключения третьего — второй общий закон логики, указанный Аристотелем:

 

 

Примеры взаимоисключающих утверждений:

1) «Сегодня будет дождь» и «Сегодня дождя не будет»;

2) «Любой треугольник правильный» и

«В каждом треугольнике есть разные стороны».

Принципы логического вывода в Прологе в отличие от традиционной формальной логики основаны на использовании предикатов. Выражение этого закона Аристотеля на языке предикатов дает конструктивную процедуру вывода конкрентых следствий из общих правил и конкретных фактов.

Закон противоречия в записи на языке исчисления предикатов преобразуется в процедуру вывода ответов на простейшие вопросы вида? А(с):

 

 

Содержательный смысл: при противоречии А(х) и не А(с) контрпримером служит х = с. Здесь х — переменная, а с — конкретное значение, при котором отрицание ответа оказывается ложным. Это значение х = с выводится системой Пролог в качестве ответа. Примеры:

? папа(х,Коля) нет — Кто папа у Коли?

? папа(х,Оля) — Кто папа у Оли?

х = Коля

? мама(х,у) — Что известно о мамах?

х = Зина у = Надя

х = Надя у = Оля

 

Закон двойного отрицания — третий общий закон формальной логики, указанный Аристотелем:

 

 

Примеры рассуждений:

 

1. Неверно, что «вчера не было дождя».

Следовательно, «вчера был дождь».

2. Неправда, что «это сделал не Саша».

Следовательно, «это сделал Саша». (?)

 

Из второго примера видно, что закон двойного отрицания является косвенным доказательством, поскольку оно не опирается на факты или аргументы. По этим причинам закон двойного отрицания может оказаться ошибочным и этот закон не является общезначимым (верным для всех случаев и ситуаций).

Правильность утверждений и рассуждений даже при безупречной логике доказательств зависит от достоверности исходных фактов и положений. Эту идею выражает четвертый общий логический закон — закон достаточных оснований, указанный Лейбницем, создателем одного из самых первых механических компьютеров и основателем исчисления предикатов.

Закон достаточных оснований:

Всякое утверждение должно предполагать существование аргументов и фактов, достаточных для его обоснования.

 

Иными словами, любое утверждение должно предполагать наличие набора фактов и правил, из которых должно вытекать утверждаемое. Нарушениями это закона являются рассуждения, опирающиеся на недостоверные факты или положения, истинность которых не проверяется, а принимается на веру.

 

Пример рассуждений, не имеющих достаточных оснований:

1.«Если дорогу перебежала черная кошка, то быть неприятностям».

2. «Это верно», потому что«это — справедливо».

Экспертные системы на ЭВМ с этой точки зрения должны создаваться на основе достоверных данных и общих правил вывода, проверенных практикой. Включение недостоверных данных или неподтвержденных обобщений и правил может привести к появлению ошибок и получению неправильных выводов.

Причина такой работы экспертных систем состоит в том, что компьютеры могут делать выводы и умозаключения только исходя из тех фактов и правил, которые введены и хранятся в ЭВМ, и только из этих данных — и ничего другого.

Интеллектуальная мощь экспертных систем на ЭВМ, также как интеллектуальный потенциал людей, связаны с возможностями накопления не только новых конретных фактических сведений, новых обобщенных сведений и знаний.

В базах знаний, экспертных системах и других системах искусственного интеллекта такие знания выражаются в форме новых понятий, записываемых в форме новых правил логического вывода.

В качестве иллюстрации дополним рассмотренную базу знаний о семье набором правил на языке Пролог, выражающих понятие «родитель»:

родитель(х,у) <- мама(х,у); — Мама — родитель.

родитель(х,у) <- папа(х,у); — Папа — родитель.

 

 

После ввода этих правил в ЭВМ система Пролог на вопросы о родителях выдаст такие ответы при указанной выше базе данных:

? родитель(Надя, х) — Кому родитель Надя?

х = Оля

х = Сережа

 

Вывод ответов на эти вопросы система Пролог проводит следующим образом. Во-первых, вопрос? родитель(Надя, х) будет заменен на отрицание не родитель(Надя, х). Далее это отрицание будет сопоставлено с правилом вывода родитель(х, у) <— мама(х, у), а затем с правилом родитель(х, у) <- папа(х, у).

Применение этой же процедуры вывода ко второму определению родитель(х,у) <- папа(х,у) даст отрицание не папа(Надя, х), означающее утверждение «Надя не является папо