
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Урок 1. Введение в алгебру логикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Элективный курс Алгебра логики
Джордж Буль
Глава 1. Алгебра логики Урок 1. Введение в алгебру логики С самого начала возникновения науки, ученые и философы задумывались над тем, как правильно мыслить. Как мыслить так, чтобы получаемые выводы были правильными, чтобы им можно было верить. Оказывается, это очень серьёзная проблема и очень часто вполне очевидные рассуждения приводят к нелепым результатам. Рассмотрим Парадокс Парикмахера: Предположим, что в некоторой деревне живут мужчины, про которых известно, что они либо бреются сами, либо их бреет парикмахер. Парикмахер живёт в этой же деревне. Вопрос: Кто бреет парикмахера? Рассуждения: Возможны два варианта ответа на поставленный вопрос: парикмахер бреется сам и его бреет кто-то другой. Рассмотрим эти два варианта: 1. Парикмахер бреется сам. Тогда он мужчина, который бреется сам, но таких мужчин парикмахер не бреет. Отсюда следует, что парикмахер себя не бреет. Получили противоречие. 2. Парикмахера бреет кто-то другой. Тогда парикмахер – мужчина, который сам не бреется, но всех таких мужчин в деревне бреет парикмахер. Отсюда следует, что парикмахер бреется сам. И мы опять получили противоречие. Оба возможных варианта привели к противоречию. Таким образом, ответа на такой, казалось простой вопрос, не существует. Заключение: самый важный вывод из всего вышесказанного – необходимо изучать мышление, так же как мы изучаем природу. Нужно открыть законы мышления, которые объясняли бы почему иногда не получается хороших выводов несмотря на то, что мы вроде мыслим правильно и как надо рассуждать, чтобы приходить к верным результатам. Нужна наука о мышлении. N Логика – это наука о формах и законах человеческого мышления. В зависимости от набора правил вывода умозаключений различают несколько вариантов логики: формальная, математическая, вероятностная, диалектическая. Формальная логика связана с анализом наших обычных содержательных рассуждений, выражаемых разговорным языком. Основоположником формальной логики является Аристотель, который впервые отделил логические формы мышления от его содержания. Математическая логика, являясь частью формальной логики, изучает только суждения и рассуждения, для которых можно однозначно решить: истинны они или ложны. Суждения и утверждения математической логики называются высказываниями и предикатами. Высказывания – это конкретные частные утверждения (2 + 3 = 5). Предикаты – это утверждения о переменных (x + y > 5). Алгебра – это наука об общих операциях, аналогичных сложению и умножению, которые выполняются не только над числами, но и над другими математическими объектами, в том числе и над высказываниями. Такая алгебра называется алгеброй логики, которая используется для математического описания работы вычислительных устройств и их программного проектирования. Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний. Алгебра логики – определенная часть математической логики, называемая исчислением высказываний. Она отвлекается от смысловой содержательности высказываний и принимает во внимание только истинность или ложность высказывания. Задачи на логические выводы. Задача 1. Ответь, правильны ли данные рассуждения? Если нет, то почему? а) Пианино – это музыкальный инструмент. У Вовы дома музыкальный инструмент. Значит, у него дома пианино. б) Классные комнаты надо проветривать. Квартира – это не классная комната. Значит, квартиру не надо проветривать. в) Если одно число при счете называют раньше, чем другое, то это число меньше. Задача 2. В ящике имеется 3 черных и 5 белых шаров. Какое наименьшее число шаров нужно взять из ящика (не заглядывая в него), чтобы среди вынутых шаров: a) оказался хотя бы один черный; b) оказался хотя бы один белый; c) оказались хотя бы два черных; d) оказались хотя бы два белых? Ответы: а) 6 шаров; б) 4 шара; в) 7 шаров; г) 5 шаров. Задача 3. Ученик собирался на вечер, когда погас свет в комнате, где в ящике шкафа лежали его коричневые и синие носки. Какое наименьшее число носков он должен взять из ящика, чтобы обеспечить себя парой одного цвета? Ответ: 3 носка. Задача 4. Сколько потребуется времени, чтобы поезд, длина которого 1 км, идущий со скоростью 60 км в час, прошел тоннель длиной в 1 км? Ответ: 2 мин. Урок 2. Основные формы мышления Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные древнегречесикими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы мышления (речи) от его содержания. N Логика - это наука о формах и способах мышления. Основными формами мышления являются: понятие, высказывание и умозаключение. Понятие выделяет существенные признаки объекта, которые отличают его от других объектов. Объекты, объединенные понятием, образуют некоторое множество. Например, понятие "компьютер" объединяет множество электронных устройств. "Автомобиль" объединяет множество механизмов, служащих для перемещения по дорогам. Вариант I. 1. Отобразить с помощью диаграммы Эйлера-Венна соотношения между следующими объемами понятий: · целые и натуральные числа. 2. Определить, что является субъектом, предикатом и связкой в следующих суждениях: · сканер- это устройство ввода информации; · атом состоит из ядра и электронов. 3. Какие предикаты первого порядка описывают условие: «Точка Х не принадлежит отрезку [A;B]»? · не(Х≥А) и Х<В; · не(Х≤B или Х≥А). 4. (Повышенный уровень сложности) Изобразите в декартовой прямоугольной системе координат область, в которой и только в которой истинен следующий предикат второго уровня: (Y ≥ X) и (Y + X ≥ 0) и (Y ≤ 1). Вариант II. 1. Отобразить с помощью диаграммы Эйлера-Венна соотношения между следующими объемами понятий: · четные и нечетные числа. 2. Определить, что является субъектом, предикатом и связкой в следующих суждениях: · клавиатура - это устройство вывода информации; · Луна является спутником Земли. 3. Какие предикаты первого порядка описывают условие: «Точка Х не принадлежит отрезку [A;B]»? · Х<А или Х>В; · Х≤А и Х≥В. 4. (Повышенный уровень сложности) Изобразите в декартовой прямоугольной системе координат область, в которой и только в которой истинен следующий предикат второго уровня: (|X| ≤ 1) и (|Y| ≤ 1). Установите, какие из следующих предложений являются логическими высказываниями, а какие — нет (объясните почему): 1. "Солнце есть спутник Земли"; 2. "2+3=4"; 3. "сегодня отличная погода"; 4. "в романе Л.Н. Толстого "Война и мир" 3 432 536 слов"; 5. "Санкт-Петербург расположен на Неве"; 6. "музыка Баха слишком сложна"; 7. "первая космическая скорость равна 7.8 км/сек"; 8. "железо — металл"; 9. "если один угол в треугольнике прямой, то треугольник будет тупоугольным"; 10. "если сумма квадратов двух сторон равен третьей, то он прямоугольный». N Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Образуем составное высказывание F, которое получится в результате конъюнкции двух простых высказываний: F=A & B. Сама функция логического умножения F может принимать лишь два значения "истина" и "ложь". Значение логической функции можно определить с помощью таблицы истинности, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов. Таблица истинности функции логического умножения
Логическая операция ДИЗЪЮНКЦИЯ: · в естественном языке соответствует союзу или; · обозначение: V; · в языках программирования обозначение: or; · иное название: логическое сложение. N Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно. Таблица истинности функции логического сложения
Логическая операция ИНВЕРСИЯ: · в естественном языке соответствует словам " Неверно, что... " и частице не; · обозначение: · в языках программирования обозначение: not; · иное название: отрицание. Таблица истинности функции логического отрицания
Логическая операция ИМПЛИКАЦИЯ: · в естественном языке соответствует обороту «Если..., то...»; · обозначение: =>; · иное название: логическое следование. N Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно. Таблица истинности функции логической импликации
Логическая операция ЭКВИВАЛЕНЦИЯ: · в естественном языке соответствует оборотам речи «Тогда и только тогда и в том и только в том случае»; · обозначение: <=>, ~; · иное название: равнозначность. N Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Таблица истинности функции логической эквиваленции
N Логические операции имеют следующий приоритет: действия в скобках, инверсия, &, V, =>, <=>. IV. Закрепление изученного Упражнение 1. Определите истинность составного высказывания:
А= {Принтер – устройство вывода информации}, B= {Процессор – устройство хранения информации}, C= {Монитор – устройство вывода информации}, D= {Клавиатура – устройство обработки информации}. Решение: сначала на основании знания устройств компьютера устанавливаем истинность простых высказываний: А=1, В=0, С=1, D=0. Определим теперь истинность составного высказывания, используя таблицы истинноcти логических операций: ( Составное высказывание ложно. Упражнение 2. Есть два простых высказывания: А – «Число 12 – четное»; В – «Антилопа – хищное животное». Составьте из них все возможные составные высказывания и определите их истинность. Ответ:
Упражнение 3. Найдите значения логических выражений: 1) F = (0 V 0) V (1 V 1) (ответ: 1) 2) F = (1 V 1) V (1 V 0) (ответ: 1) 3) F = (0 & 0) & (1 & 1) (ответ: 0) 4) F = 5) F = ( Задача 1. Из двух простых высказываний постройте сложное высказывание, используя логические связки «И» и «ИЛИ». Запишите логические высказывания с помощью логических операций и определите их истинность. 1. Антон младше Саши. Наташа старше Антона. 2. Один десятый класс идет на экскурсию в музей. Второй десятый класс идет в театр. 3. На полке стоят учебники. На полке стоят справочники. 4. Часть детей – девочки. Остальные – мальчики. Задача 2. Какое логическое выражение соответствует высказыванию: «Точка Х принадлежит интервалу (А, В)». 1. (Х < A) или (X > B) 2. (X > A) и (X < B) 3. не(X < A) или (X < B) 4. (X > A) или (X > B)
Возможна и другая логика. «Человек не знал двух слов – да и нет. Он отвечал гуманно: Может быть, возможно, мы подумаем…». Эту запись находим на страницах знаменитых «Записных книжек» замечательного писателя Ильи Ильфа (одного из соавторов романа «Двенадцать стульев» и «Золотой теленок»). И в самом деле, часто нам явно не хватает двух известных слов, точнее, двух логических значений. Ведь то и дело мы слышим высказывания, про которые нельзя сказать, истинны они или ложны. «Возможно, я получу на экзамене отличную оценку». Или, например, обычной является ситуация, когда мы должны принять решение – делать что-либо или нет, не имея при этом всей необходимой информации либо не зная степени ее достоверности. Ученые давно пытались преодолеть ограничения классической Аристотелевой логики. Например, русский логик Н.А.Васильев в 1910 г. разработал оригинальную систему, назвав её «воображаемой логикой». Согласно Васильеву, каждое суждение может быть утвердительным, отрицательным или акцидентальным. Если акцидентальное суждение истинно, то и утвердительное, и отрицательное суждения являются ложными. Тем не менее одно и то же суждение не может быть одновременно и истинным, и ложным. Логика Васильева не имела большой известности и только в последние годы учёные вновь стали обращаться к его идеям. Зато самое широкое распространение получили так называемые многозначные логики. В них значение истинности переменных и функций располагаются в диапазоне от 0 до k-1 (тогда 0 можно понимать как абсолютную ложь, а k-1 как абсолютную истину).Основоположником новой науки стал польский математик Ян Лусакевич (1878-1956), предложивший в 1920г. трехзначную логику. В логике Лукасевича значения могли быть истинными и нейтральными. Спустя год американский ученый Эмиль Пост (1897-1954) создал ее обобщенную модель – k- значную логику. Еще позднее, в 1930 г., Ян Лукасевич и Альфред Тарский (1920 – 1983) разработали бесконечную логику. Для многозначных логик также можно определять алгебры, подобные булевой. Для k-значной логики операции отрицания, конъюнкции и дизъюнкции можно задать следующим образом:
Х1 V X2 = min(X1, X2), X1 & X2 = max(X1, X2). Для двузначной логики, то есть для случая k=2, это определение приводит к уже известным булевым операциям. Задачи для самостоятельного решения
Модельные ответы:
Урок 5. Таблицы истинности Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных. N Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания. Алгоритм построения таблицы истинности: 1. подсчитать количество переменных n в логическом выражении; 2. определить число строк в таблице m = 2n; 3. подсчитать количество логических операций в формуле; 4. установить последовательность выполнения логических операций с учетом скобок и приоритетов; 5. определить количество столбцов в таблице: число переменных плюс число операций; 6. выписать наборы входных переменных с учетом того, что они представляют собой натуральный ряд n-разрядных двоичных чисел от 0 до 2 n —1; 7. провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной в п.4 последовательностью. Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом: а) определить количество наборов входных переменных; б) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю —1; в) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами 0 или 1, начиная с группы 0; г) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа. Упражнение 1. Построим таблицу истинности для выражения F=(A V B) & ( Решение. 1. Количество строк = 22 (2 переменных) + 1 (заголовки столбцов) = 5 2. Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (V, &,, V,) = 7. 3. Расставим порядок выполнения операций: 1 5 2 4 3. (A V B) & ( 4. Построим таблицу:
Упражнение 2. Построим таблицу истинности для логического выражения F=X V Y & Решение. 1. Количество строк = 23 + 1 = 9. 2. Количество столбцов = 3 логические переменные + 3 логических операций = 6. 3. Укажем порядок действий: 3 2 1 X V Y & 4. Нарисуем и заполним таблицу:
Упражнение 3. Для формулы F= A & (B V Решение. 1. Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8. 2. Количество логических операций в формуле 5, следовательно, количество столбцов в таблице истинности должно быть 3 + 5 = 8. 3. Укажем порядок действий: 5 4 1 3 2 A & (B V
Урок 6. Логические законы В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы. 1. Закон двойного отрицания: А = Двойное отрицание исключает отрицание. 2. Переместительный (коммутативный) закон: — для логического сложения: А V B = B V A; — для логического умножения: A&B = B&A. Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания. В обычной алгебре a + b = b + a, a * b = b * a. 3. Сочетательный (ассоциативный) закон: — для логического сложения: (A V B) V C = A V (B V C); — для логического умножения: (A & B) & C = A & (B & C). При одинаковых знаках скобки можно ставить произвольно или вообще опускать. В обычной алгебре: (a + b) + c = a + (b + c) = a + b + c, (а * b) * c = a * (b * c) = a * b * c. 4. Распределительный (дистрибутивный) закон: — для логического сложения: (A V B)&C = (A&C) V (B&C); — для логического умножения: (A & B) V C = (A V C) & (B V C). Определяет правило выноса общего высказывания за скобку. В обычной алгебре: (a + b) * c = a * c + b * c. 5. Закон общей инверсии (законы де Моргана): — для логического сложения
— для логического умножения:
_______ __ (A => B) = A & B А => B = 6. Закон идемпотентности (от латинских слов idem — тот же самый и potens —сильный; дословно — равносильный): — для логического сложения: A V A = A; — для логического умножения: A & A = A. Закон означает отсутствие показателей степени. 7. Законы исключения констант: — для логического сложения: A V 1 = 1, A V 0 = A; — для логического умножения: A & 1 = A, A & 0 = 0. 8. Закон противоречия: A & Невозможно, чтобы противоречащие высказывания были одновременно истинными. 9. Закон исключения третьего: A V Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано. 10. Закон поглощения: — для логического сложения: A V (A & B) = A; — для логического умножения: A & (A V B) = A. 11. Закон исключения (склеивания): — для логического сложения: (A & B) V ( — для логического умножения: (A V B)&( 12. Закон контрапозиции (правило перевертывания): (A <=> B) = (B <=> A). Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут. Законы логики
Упражнение 1. Упростите логическое выражение F=(A V B V C) & Правильность упрощения проверьте с помощью таблиц истинности для исходного и полученного логического выражения. Решение. (A V B V C) & Согласно распределительному закону для логического сложения: (A V B V C) & ( Согласно закону противоречия: (A & Согласно закону идемпотентности: (B & B) = B. Подставляем значения и, используя переместительный (коммутативный) закон и группируя слагаемые, получаем: 0 V (A & B) V ( Согласно закону исключения (склеивания): (A & B) V ( Подставляем значения и получаем: 0 V B V B V B V (C & Согласно закону исключения констант для логического сложения и закону идемпотентности: 0 V B V B V B V 0 = B. Согласно распределительному (дистрибутивному) закону для логического умножения:  ) V (A & ) V (A &  ) = (С V A) & (C V ) = (С V A) & (C V  ) & ( ) & ( V A) & ( V A) & ( V V  ). ).
Согласно закону исключения третьего: (C V Подставляем значения и окончательно получаем: F = B & Проверим правильность преобразования логического выражения с использованием электронной таблицы EXCEL. Для этого необходимо запустить Microsoft Excel и построить таблицу истинности для исходного и конечного логических выражений. После ввода аргументов и формул на листе появится таблица истинности логического выражения. Сравнить последние столбцы в таблицах между собой.
Найдите Х, если Решение.  V V  = ( = ( & &  ) V ( ) V ( & &  ) = ( ) = ( & &  ) V ( ) V ( & A) = & A) =  &( &( V A) = V A) =  &1 = &1 =  . .
Полученную левую часть приравняем правой:
Окончательно получим: Х = IV. Закрепление материала (самостоятельная работа) Упражнение 3. Упростите логические выражения: 1. F= A & B V 2. F = ( (ответ: Урок 7. Правила преобразования логических выражений 1. Правила преобразования логических выражений. Если логическое выражение содержит большое число о
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.220.239 (0.013 с.) |


 ;
;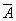
 &
&  ) & (C V D), состоящего из простых высказываний:
) & (C V D), состоящего из простых высказываний: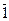 &
&  ) & (1 V 0) = (0 & 1) & (1 V 0) = 0
) & (1 V 0) = (0 & 1) & (1 V 0) = 0 =(k-1)-Х,
=(k-1)-Х, . ______________________________________________________
______________________________________________________
______________________________________________________
. ______________________________________________________
______________________________________________________
______________________________________________________
 1.Логика
1.Логика
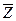 .
. &
& 
 .
.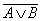 =
=  =
=  =
=  .
. Упражнение 2.
Упражнение 2. V B &
V B & 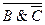 ).
).


