Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Урок 14. Переключательные схемыСодержание книги
Поиск на нашем сайте
Что такое переключательная схема? В компьютерах и других автоматических устройствах широко применяются электрические схемы, содержащие сотни и тысячи переключательных элементов: реле, выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что здесь с успехом может быть использован аппарат алгебры логики. I Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал. Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю. Будем считать, что два переключателя Х и Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нулю — если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости. Найдем функции проводимости F некоторых переключательных схем: a) Схема не содержит переключателей и проводит ток всегда, следовательно F=1; б) Схема содержит один постоянно разомкнутый контакт, следовательно F=0; в) Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x; г) Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(x) = д)
е)
Схема проводит ток, когда хотя бы один из переключателей замкнут, следовательно, F(x)=x v y; ж)
N Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале). N Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей. Задача нахождения среди равносильных схем наиболее простых является очень важной. Большой вклад в ее решение внесли российские учёные Ю.И. Журавлев, С.В. Яблонский и др. При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы. СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём этапам: 1. составлению функции проводимости по таблице истинности, отражающей эти условия; 2. упрощению этой функции; 3. построению соответствующей схемы. АНАЛИЗ СХЕМЫ сводится к: 1. определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных. 2. получению упрощённой формулы. Упражнение 1. Построим схему, содержащую 4 переключателя x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных трёх контактов. Решение. В этом случае можно обойтись без построения таблицы истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) = t. (x v y v z), а схема выглядит так:
Упражнение 2. Построим схему с пятью переключателями, которая проводит ток в том и только в том случае, когда замкнуты ровно четыре из этих переключателей.
Схема имеет вид:
Упражнение 3. Найдем функцию проводимости схемы:
Решение. Имеется четыре возможных пути прохождения тока при замкнутых переключателях a, b, c, d, e: через переключатели a, b; через переключатели a, e, d; через переключатели c, d и через переключатели c, e, b. Функция проводимости F(a, b, c, d, e) = a. b v a. e. d v c. d v c. e. b. Урок 15. Сумматор и триггер Полусумматор. Сумматор. Логические схемы используются в вычислительной технике: 1. Для реализации выполнения математических операций; 2. Для хранения информации. Как это он делает? Рассмотрим на уроке. Итак, как процессор выполняет математические операции? Прежде всего, обратите внимание на следующие моменты: · Каким образом должна быть представлена информация, чтобы с ней мог работать компьютер? (В двоичном коде, т.е. в виде 0 и 1) · Чтобы компьютер мог выполнять математические операции с числами, в какой системе счисления они должны быть представлены? (В двоичной) · Почему? (Потому что двоичную систему счисления наиболее просто реализовать в технических устройствах) · Какие сигналы подаются на входы логических вентилей? (0 и 1) Вывод: таким образом и в двоичной системе счисления и в алгебре логики информация представлена в виде двоичных кодов. И второй момент. Для того чтобы максимально упростить работу компьютера, все математические операции (вычитание, деление, умножение и т.д.) сводятся к сложению. Вспомним таблицу сложения двоичных чисел. Запишем ее в несколько иной форме:
Обратите внимание на дополнительный столбец. Его мы ввели потому, что при сложении происходит перенос в старший разряд. Обозначим его P и закончим заполнение таблицы:
Проанализируем полученный результат. · Таблице истинности какой логической функции аналогичен столбец P? (Логическое умножение) · Таблице истинности какой логической функции аналогичен столбец S? (Логическое сложение, кроме случая, когда на входы подаются две единицы) Логическое выражение, по которому можно определить сумму S, записывается следующим образом: S = (A V B) & Построим к этому логическому выражению логическую схему:
Проследим за изменением сигнала при прохождении через схему:
С какого элемента можно снимать сигнал Р, если мы выяснили, что результат Р соответствует логическому умножению? (С первого вентиля, реализующего операцию конъюнкции)
Полученная нами схема выполняет сложение двоичных одноразрядных чисел и называется полусумматором, так как не учитывает перенос из младшего разряда в старший (выход Р). Для учета переноса из младшего разряда необходимы два полусумматора. Более «умным» является устройство, которое при сложении учитывает перенос из младшего разряда. Называется оно полный одноразрядный сумматор. N Сумматор – это логическая электронная схема, выполняющая сложение двоичных чисел. Сумматор является главной частью процессора. Рассмотрим принцип работы одноразрядного двоичного сумматора. Одноразрядный сумматор должен иметь три входа: A, B –слагаемые и Р0 – перенос из предыдущего разряда и выходы: S – сумма и Р – перенос. Нарисуем одноразрядный сумматор в виде единого функционального узла:
Построим таблицу сложения:
Логические выражения для Р и S будут иметь следующий вид: S = (A V B V P0) & P = (A & B) V (A & P0) V (B & P0). Но процессор, как правило, складывает многоразрядные двоичные числа. Например, 1012+1102=10112. Для того чтобы вычислить сумму n-разрядных двоичных чисел, необходимо использовать многоразрядный сумматор, в котором на каждый разряд ставится одноразрядный сумматор и выход-перенос сумматора младшего разряда подключается к входу сумматора старшего разряда.
Упражнение 1. Проследите на схеме за изменением сигнала на примере сложения 1012+1102=10112. Триггер Триггер ( trigger – защелка, спусковой крючок) – это устройство, позволяющее запоминать, хранить и считывать информацию. Каждый триггер хранит 1 бит информации, т.е. он может находиться в одном из двух устойчивых состояний – логический «0» или логическая «1». Триггер способен почти мгновенно переходить из одного электрического состояния в другое и наоборот.
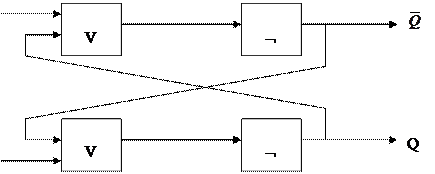
Логическая схема триггера выглядит следующим образом:
Входы триггера расшифровываются следующим образом – S (от английского Set –установка) и R (Reset – сброс). Они используются для установки триггера в единичное состояние и сброса в нулевое. В связи с этим такой триггер называется RS-триггер. Выход Q называется прямым, а противоположный – инверсный. Сигналы на прямом и инверсном выходах, конечно же, должны быть противоположны. Рассмотрим, как работает эта схема. Пусть для определенности на вход S подан единичный сигнал, а R=0. Тогда независимо от состояния другого входа, который подсоединен к выходу Q (иначе говоря, вне зависимости от предыдущего состояния триггера), верхний по схеме элемент ИЛИ-НЕ получит на выходе 0 (результат ИЛИ, естественно, равен 1, но его инверсия – 0). Этот нулевой сигнал передается на вход другого логического элемента, где на втором входе R тоже установлен 0. В итоге после выполнения логических операций ИЛИ-НЕ над двумя входными нулями этот элемент получает на выходе 1, которую возвращает первому элементу на соответствующий вход. Последнее обстоятельство очень важно: теперь, когда на этом входе установилась 1, состояние другого входа (S) больше не играет роли. Иными словами, если даже теперь убрать входной сигнал S, внутреннее распределение уровней сохранится без изменения. Поскольку согласно нашим рассуждениям Q=1, триггер перешел в единичное состояние, и пока не придут новые сигналы, сохраняет его. Итак, при подаче сигнала на вход S триггер переходит в устойчивое единичное состояние. При противоположной комбинации сигналов R=1 и S=0 вследствие полной симметрии схемы все происходит совершенно аналогично, но теперь на выходе Q уже получается 0. Иными словами, при подаче сигнала на вход R-триггер сбрасывается в устойчивое нулевое состояние. Особо отметим, что окончание действия сигнала в обоих случаях приводит к тому, что R=0 и S=0. Мы видели, что при этом триггер сохраняет на выходе Q тот сигнал, который был установлен входным импульсом (S или R). Отсюда такой режим часто называют режимом хранения информации. Итак, при отсутствии входных сигналов триггер сохраняет последнее занесенное в него значение сколь угодно долго. Оставшийся режим S=1 и R=1, когда сигнал подается на оба входа одновременно, считается запрещенным, поскольку в этом случае после снятия входных сигналов (особенно одновременного!) результат непредсказуем. В ходе объяснения заполняется таблица:
Итак, мы выяснили, как работает триггер. Без преувеличения триггер является одним из существенных узлов при проектировании ЭВМ. Так как триггер может хранить только 1 бит информации, то несколько триггеров объединяют вместе. Полученное устройство называется регистром. Регистры содержатся во всех вычислительных узлах компьютера – начиная с центрального процессора, памяти и заканчивая периферийными устройствами, и позволяют также обрабатывать информацию. В регистре может быть 8, 16, 32 или 64 триггера.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 4166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.103.203 (0.008 с.) |

 связаны таким образом, что когда Х замкнут, то
связаны таким образом, что когда Х замкнут, то  .
.




 Схема проводит ток, когда оба переключателя замкнуты, следовательно, F(x) = x. y;
Схема проводит ток, когда оба переключателя замкнуты, следовательно, F(x) = x. y;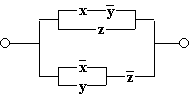
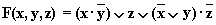 Схема состоит из двух параллельных ветвей и описывается функцией:
Схема состоит из двух параллельных ветвей и описывается функцией:



 .
.



 V(A & B & P0).
V(A & B & P0).