
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Урок 3. Алгебра высказыванийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание. N Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием. N Высказывание, состоящее из простых высказываний, называются составным (сложным). Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами: А = {Аристотель - основоположник логики} В = {На яблонях растут бананы}. Обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания: "Сумма углов треугольника равна 180 градусам" устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным. Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0. Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами. Теперь можно определить понятия логической переменной, логической функции и логической операции. N Логическая переменная – это простое высказывание, содержащее только одну мысль. Ее символическое обозначение – латинская буква (например, А, В, Х, Y и т.д.). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0). N Л огическая функция – это составное высказывание, которая содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Ее символическое обозначение F(A, B, …). На основании простых высказываний могут быть построены составные высказывания. Над высказываниями можно производить логические операции, в результате которых получаются новые, составные высказывания. Для образования новых высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок "и", "или", "не". Упражнение 1. Выделите в составных высказываниях простые. Обозначьте каждое из них буквой. · если компьютер включен, то на нем можно работать; · если завтра будет хорошая погода, то мы пойдем купаться; · он хорошо ухаживал за цветами, поэтому они выросли большими и красивыми; · ты можешь купить в магазине продукты, если у тебя есть деньги. Ответы: · А="компьютер включен", В="на нем можно работать"; · А="завтра будет хорошая погода", В="мы пойдем купаться"; · А="он хорошо ухаживал за цветами", В="они выросли большими и красивыми"; · А="ты можешь купить в магазине продукты", В="у тебя есть деньги". Упражнение 2. Даны простые высказывания. Составьте из них всевозможные составные высказывания. А= «Идет дождь»; В= «Взять зонтик»; С= «В лесу появятся грибы»; D= «Уровень воды в реке повысится». Модельные ответы: «Идет дождь, поэтому я возьму зонтик». «Если идет дождь, значит в лесу появятся грибы и уровень воды в реке повысится». «Уровень воды в реке повысится, потому что идет дождь». Упражнение 3. (самостоятельная работа) Ниже приведена таблица, левая колонка которой содержит основные логические союзы (связки), с помощью которых в естественном языке строятся сложные высказывания. Заполните правую колонку сложными высказываниями с соответствующими союзами.
Урок 4. Логические операции алгебры высказываний Логическая операция КОНЪЮНКЦИЯ: · в естественном языке соответствует союзу и; · обозначение: &; · в языках программирования обозначение: and; · иное название: логическое умножение. N Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Образуем составное высказывание F, которое получится в результате конъюнкции двух простых высказываний: F=A & B. Сама функция логического умножения F может принимать лишь два значения "истина" и "ложь". Значение логической функции можно определить с помощью таблицы истинности, которая показывает, какие значения принимает логическая функция при всех возможных наборах ее аргументов. Таблица истинности функции логического умножения
Логическая операция ДИЗЪЮНКЦИЯ: · в естественном языке соответствует союзу или; · обозначение: V; · в языках программирования обозначение: or; · иное название: логическое сложение. N Дизъюнкция - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно. Таблица истинности функции логического сложения
Логическая операция ИНВЕРСИЯ: · в естественном языке соответствует словам " Неверно, что... " и частице не; · обозначение: · в языках программирования обозначение: not; · иное название: отрицание. N Отрицание - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается. Таблица истинности функции логического отрицания
Логическая операция ИМПЛИКАЦИЯ: · в естественном языке соответствует обороту «Если..., то...»; · обозначение: =>; · иное название: логическое следование. N Импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно. Таблица истинности функции логической импликации
Логическая операция ЭКВИВАЛЕНЦИЯ: · в естественном языке соответствует оборотам речи «Тогда и только тогда и в том и только в том случае»; · обозначение: <=>, ~; · иное название: равнозначность. N Эквиваленция – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Таблица истинности функции логической эквиваленции
N Логические операции имеют следующий приоритет: действия в скобках, инверсия, &, V, =>, <=>. IV. Закрепление изученного Упражнение 1. Определите истинность составного высказывания:
А= {Принтер – устройство вывода информации}, B= {Процессор – устройство хранения информации}, C= {Монитор – устройство вывода информации}, D= {Клавиатура – устройство обработки информации}. Решение: сначала на основании знания устройств компьютера устанавливаем истинность простых высказываний: А=1, В=0, С=1, D=0. Определим теперь истинность составного высказывания, используя таблицы истинноcти логических операций: ( Составное высказывание ложно. Упражнение 2. Есть два простых высказывания: А – «Число 12 – четное»; В – «Антилопа – хищное животное». Составьте из них все возможные составные высказывания и определите их истинность. Ответ:
Упражнение 3. Найдите значения логических выражений: 1) F = (0 V 0) V (1 V 1) (ответ: 1) 2) F = (1 V 1) V (1 V 0) (ответ: 1) 3) F = (0 & 0) & (1 & 1) (ответ: 0) 4) F = 5) F = ( Задача 1. Из двух простых высказываний постройте сложное высказывание, используя логические связки «И» и «ИЛИ». Запишите логические высказывания с помощью логических операций и определите их истинность. 1. Антон младше Саши. Наташа старше Антона. 2. Один десятый класс идет на экскурсию в музей. Второй десятый класс идет в театр. 3. На полке стоят учебники. На полке стоят справочники. 4. Часть детей – девочки. Остальные – мальчики. Задача 2. Какое логическое выражение соответствует высказыванию: «Точка Х принадлежит интервалу (А, В)». 1. (Х < A) или (X > B) 2. (X > A) и (X < B) 3. не(X < A) или (X < B) 4. (X > A) или (X > B)
Возможна и другая логика. «Человек не знал двух слов – да и нет. Он отвечал гуманно: Может быть, возможно, мы подумаем…». Эту запись находим на страницах знаменитых «Записных книжек» замечательного писателя Ильи Ильфа (одного из соавторов романа «Двенадцать стульев» и «Золотой теленок»). И в самом деле, часто нам явно не хватает двух известных слов, точнее, двух логических значений. Ведь то и дело мы слышим высказывания, про которые нельзя сказать, истинны они или ложны. «Возможно, я получу на экзамене отличную оценку». Или, например, обычной является ситуация, когда мы должны принять решение – делать что-либо или нет, не имея при этом всей необходимой информации либо не зная степени ее достоверности. Ученые давно пытались преодолеть ограничения классической Аристотелевой логики. Например, русский логик Н.А.Васильев в 1910 г. разработал оригинальную систему, назвав её «воображаемой логикой». Согласно Васильеву, каждое суждение может быть утвердительным, отрицательным или акцидентальным. Если акцидентальное суждение истинно, то и утвердительное, и отрицательное суждения являются ложными. Тем не менее одно и то же суждение не может быть одновременно и истинным, и ложным. Логика Васильева не имела большой известности и только в последние годы учёные вновь стали обращаться к его идеям. Зато самое широкое распространение получили так называемые многозначные логики. В них значение истинности переменных и функций располагаются в диапазоне от 0 до k-1 (тогда 0 можно понимать как абсолютную ложь, а k-1 как абсолютную истину).Основоположником новой науки стал польский математик Ян Лусакевич (1878-1956), предложивший в 1920г. трехзначную логику. В логике Лукасевича значения могли быть истинными и нейтральными. Спустя год американский ученый Эмиль Пост (1897-1954) создал ее обобщенную модель – k- значную логику. Еще позднее, в 1930 г., Ян Лукасевич и Альфред Тарский (1920 – 1983) разработали бесконечную логику. Для многозначных логик также можно определять алгебры, подобные булевой. Для k-значной логики операции отрицания, конъюнкции и дизъюнкции можно задать следующим образом:
Х1 V X2 = min(X1, X2), X1 & X2 = max(X1, X2). Для двузначной логики, то есть для случая k=2, это определение приводит к уже известным булевым операциям. Задачи для самостоятельного решения
Модельные ответы:
Урок 5. Таблицы истинности Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных. N Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания. Алгоритм построения таблицы истинности: 1. подсчитать количество переменных n в логическом выражении; 2. определить число строк в таблице m = 2n; 3. подсчитать количество логических операций в формуле; 4. установить последовательность выполнения логических операций с учетом скобок и приоритетов; 5. определить количество столбцов в таблице: число переменных плюс число операций; 6. выписать наборы входных переменных с учетом того, что они представляют собой натуральный ряд n-разрядных двоичных чисел от 0 до 2 n —1; 7. провести заполнение таблицы истинности по столбикам, выполняя логические операции в соответствии с установленной в п.4 последовательностью. Наборы входных переменных, во избежание ошибок, рекомендуют перечислять следующим образом: а) определить количество наборов входных переменных; б) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки 0, а нижнюю —1; в) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами 0 или 1, начиная с группы 0; г) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами 0 или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа. Упражнение 1. Построим таблицу истинности для выражения F=(A V B) & ( Решение. 1. Количество строк = 22 (2 переменных) + 1 (заголовки столбцов) = 5 2. Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (V, &,, V,) = 7. 3. Расставим порядок выполнения операций: 1 5 2 4 3. (A V B) & ( 4. Построим таблицу:
Упражнение 2. Построим таблицу истинности для логического выражения F=X V Y & Решение. 1. Количество строк = 23 + 1 = 9. 2. Количество столбцов = 3 логические переменные + 3 логических операций = 6. 3. Укажем порядок действий: 3 2 1 X V Y & 4. Нарисуем и заполним таблицу:
Упражнение 3. Для формулы F= A & (B V Решение. 1. Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 23 = 8. 2. Количество логических операций в формуле 5, следовательно, количество столбцов в таблице истинности должно быть 3 + 5 = 8. 3. Укажем порядок действий: 5 4 1 3 2 A & (B V
Урок 6. Логические законы В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы. 1. Закон двойного отрицания: А = Двойное отрицание исключает отрицание. 2. Переместительный (коммутативный) закон: — для логического сложения: А V B = B V A; — для логического умножения: A&B = B&A. Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания. В обычной алгебре a + b = b + a, a * b = b * a. 3. Сочетательный (ассоциативный) закон: — для логического сложения: (A V B) V C = A V (B V C); — для логического умножения: (A & B) & C = A & (B & C). При одинаковых знаках скобки можно ставить произвольно или вообще опускать. В обычной алгебре: (a + b) + c = a + (b + c) = a + b + c, (а * b) * c = a * (b * c) = a * b * c. 4. Распределительный (дистрибутивный) закон: — для логического сложения: (A V B)&C = (A&C) V (B&C); — для логического умножения: (A & B) V C = (A V C) & (B V C). Определяет правило выноса общего высказывания за скобку. В обычной алгебре: (a + b) * c = a * c + b * c. 5. Закон общей инверсии (законы де Моргана): — для логического сложения
— для логического умножения:
_______ __ (A => B) = A & B А => B = 6. Закон идемпотентности (от латинских слов idem — тот же самый и potens —сильный; дословно — равносильный): — для логического сложения: A V A = A; — для логического умножения: A & A = A. Закон означает отсутствие показателей степени. 7. Законы исключения констант: — для логического сложения: A V 1 = 1, A V 0 = A; — для логического умножения: A & 1 = A, A & 0 = 0. 8. Закон противоречия: A & Невозможно, чтобы противоречащие высказывания были одновременно истинными. 9. Закон исключения третьего: A V Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано. 10. Закон поглощения: — для логического сложения: A V (A & B) = A; — для логического умножения: A & (A V B) = A. 11. Закон исключения (склеивания): — для логического сложения: (A & B) V ( — для логического умножения: (A V B)&( 12. Закон контрапозиции (правило перевертывания): (A <=> B) = (B <=> A). Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут. Законы логики
Упражнение 1. Упростите логическое выражение F=(A V B V C) & Правильность упрощения проверьте с помощью таблиц истинности для исходного и полученного логического выражения. Решение. (A V B V C) & Согласно распределительному закону для логического сложения: (A V B V C) & ( Согласно закону противоречия: (A & Согласно закону идемпотентности: (B & B) = B. Подставляем значения и, используя переместительный (коммутативный) закон и группируя слагаемые, получаем: 0 V (A & B) V ( Согласно закону исключения (склеивания): (A & B) V ( Подставляем значения и получаем: 0 V B V B V B V (C & Согласно закону исключения констант для логического сложения и закону идемпотентности: 0 V B V B V B V 0 = B. Согласно распределительному (дистрибутивному) закону для логического умножения:  ) V (A & ) V (A &  ) = (С V A) & (C V ) = (С V A) & (C V  ) & ( ) & ( V A) & ( V A) & ( V V  ). ).
Согласно закону исключения третьего: (C V Подставляем значения и окончательно получаем: F = B & Проверим правильность преобразования логического выражения с использованием электронной таблицы EXCEL. Для этого необходимо запустить Microsoft Excel и построить таблицу истинности для исходного и конечного логических выражений. После ввода аргументов и формул на листе появится таблица истинности логического выражения. Сравнить последние столбцы в таблицах между собой.
Найдите Х, если Решение.  V V  = ( = ( & &  ) V ( ) V ( & &  ) = ( ) = ( & &  ) V ( ) V ( & A) = & A) =  &( &( V A) = V A) =  &1 = &1 =  . .
Полученную левую часть приравняем правой:
Окончательно получим: Х = IV. Закрепление материала (самостоятельная работа) Упражнение 3. Упростите логические выражения: 1. F= A & B V 2. F = ( (ответ: Урок 7. Правила преобразования логических выражений 1. Правила преобразования логических выражений. Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести к нормальной форме. Формула имеет нормальную форму, если в ней отсутствуют: · знаки эквивалентности; · знаки импликации; · двойного отрицания; · знаки отрицания находятся только при логических переменных. Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.). Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул: 1)
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами); 2)
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией); 3)
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания); 4)
(вводится вспомогательный логический сомножитель ( 5)
(сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
6)
(выносятся за скобки общие множители; применяется правило операций с константами); 7)
(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания); 8)
(общий множитель x выносится за скобки, комбинируются слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции 9)
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции); 10) (используются правило де Моргана, закон двойно
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 2006; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 ;
;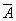
 &
&  ) & (C V D), состоящего из простых высказываний:
) & (C V D), состоящего из простых высказываний: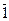 &
&  ) & (1 V 0) = (0 & 1) & (1 V 0) = 0
) & (1 V 0) = (0 & 1) & (1 V 0) = 0 =(k-1)-Х,
=(k-1)-Х, . ______________________________________________________
______________________________________________________
______________________________________________________
. ______________________________________________________
______________________________________________________
______________________________________________________
 1.Логика
1.Логика
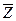 .
. &
& 
 .
.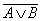 =
=  =
=  =
=  .
. Упражнение 2.
Упражнение 2. V B &
V B & 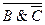 ).
).



 ); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);


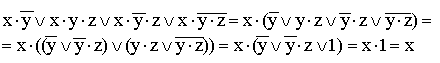
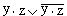 применяется правило операции переменной с её инверсией);
применяется правило операции переменной с её инверсией);




