Урок 11. Решение логических задач средствами алгебры логики

Следующие логические задачи мы решим с помощью средств алгебры логики.

Задача 1. Представим такую ситуацию: по телевизору с иноптик объявляет прогноз погоды на завтра и утверждает следующее:

1. Если не будет ветра, то будет пасмурная погода без дождя.

2. Если будет дождь, то будет пасмурно и без ветра.

3. Если будет пасмурная погода, то будет дождь и не будет ветра.

Так какая же погода будет завтра?

Решение:

а ) Выделим простые высказывания и запишем их через переменные:

A – «Ветра нет»

B – «Пасмурно»

С – «Дождь»

б) Запишем логические функции (сложные высказывания) через введенные переменные:

1. Если не будет ветра, то будет пасмурная погода без дождя:

__

A → B & C

 

2. Если будет дождь, то будет пасмурно и без ветра:

С → B & A

 

3. Если будет пасмурная погода, то будет дождь и не будет ветра

B → C & A

в) Запишем произведение указанных функций:

_

F=(A→ B & C) & (C→B & A) & (B→ C & A)

г) Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия):

_

F=(A→ B & C) & (C→B & A) & (B→ C & A) =

_ _ _ _

= (A v B & C) & (C v B&A) & (B v C&A) =

_ _ _ _

= (A v B & C) & (B v C&A) & (C v B&A) =

_ _ _ _ _ _

= (A & B v B&C&B v A&C&A v B&C&C&A) & (C v B&A)=

_ _ _ _ _ _ _

= A & B &(C v B&A) =A&B&C v A&B&B&A =

_ _ _

= A&B&C

д) Приравняем результат единице, т.е. наше выражение должно быть истинным:

_ _ _

F = A & B & C = 1

 

е) Проанализируем результат:

Логическое произведение равно 1, если каждый множитель равен 1.

Поэтому:

 

_ _ _

A = 1; B = 1; C = 1;

Значит: A = 0; B = 0; C = 0;

Ответ: погода будет ясная, без дождя, но ветреная.

Задача 2. Трое друзей, болельщиков автогонок "Формула-1", спорили о результатах предстоящего этапа гонок.

— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.

— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.

Питер, к которому обратился Ник, возмутился:

— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.

По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?

Решение.

Введем обозначения для логических высказываний:

Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.

Реплика Ника "Алези пилотирует самую мощную машину" не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.

Зафиксируем высказывания каждого из друзей:

Джон: & X;

Ник: Ш & ;

Питер: .

Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание _______

( & X) & (Ш & ) & V ( & X) & & V ( & X) & (Ш & ) & =

= (Ш V ) & Ш & & = Ш & & .

Высказывание Ш & & истинно только при Ш=1, А=0, Х=0.

Ответ: победителем этапа гонок стал Шумахер.

Задача 2. (самостоятельная работа)

Андрею, Саше и Егору предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Андрей показал, что преступники скрылись на синем Мерседесе, Саша сказал, что это был черный Джип, а Егор утверждал, что это был Форд Мустанг и ни в коем случае не синий. Стало известно, что желая запутать следствие, каждый из них указал правильно либо марку машины, либо только ее цвет. Какого цвета и какой марки была машина?

Глава III. Связь между алгеброй логики и двоичным кодированием

Логические схемы

Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880-1933), кстати, несколько лет работавший в России, писал еще в 1910 году: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить:

1. будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции;

2. не содержит ли она излишних усложнений.

Созданная позднее М.А.Гавриловым (1903-1979) теория релейно-контактных схем показала, что это вовсе не утопия.

Посмотрим на микросхему. На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.

С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет…В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка тоже работает на электричестве). Для этого рассмотрим электрические контактные схемы, реализующие логические операции.

Схема 1

Схема 2

А     Схема 3

 

На рисунках контакты обозначены латинскими буквами А и В. Введем обозначение: 1 – контакт замкнут, 0 – контакт разомкнут. Цепь на схеме 1 с последовательным соединением контактов соответствует логической операции «И». Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ». Цепь на схеме 3 соответствует логической операции «НЕ».

Докажем это, рассмотрев состояния схем при различных состояниях контактов.

Попросите детей приготовить в тетради таблицу:

Конъюнкция	Дизъюнкция	Инверсия

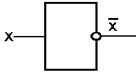
Заполняйте ее по ходу объяснения материала.

Схема 1. (составляем таблицу истинности).

1. Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.

2. Первый контакт в положении «вкл», второй – в положении «выкл». Ток не идет, лампочка не горит.

3. Обратная ситуация. Лампочка не горит.

4. Оба контакта в положении выкл». Тока нет. Лампочка не горит.

Вывод: первая схема действительно реализует логическую операцию «И».

Схема 2. (составляем таблицу истинности).

1. Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.

2. Первый контакт в положении «вкл», второй – в положении «выкл». Ток идет, лампочка горит.

3. Обратная ситуация. Лампочка горит.

4. Оба контакта в положении выкл». Тока нет. Лампочка не горит.

Вывод: вторая схема действительно реализует логическую операцию «ИЛИ».

Схема 3. (составляем таблицу истинности).

В этом устройстве в качестве переключателя используется автоматический ключ. Когда тока на нем нет, пластинка замыкает контакты и лампочка горит. Если на ключ подать напряжение, то вследствие явления электромагнитной индукции пластинка прижимается и цепь размыкается. Лампочка не горит.

Вывод: третья первая схема действительно реализует логическую операцию «НЕ».

Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ. Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента.

Их названия (конъюнктор, дизъюнктор, инвертор) и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико.

Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.

Заполненная таблица:

Конъюнкция	Дизъюнкция	Инверсия
Схема 1	Схема 2	X     Схема 3
Х Y Результат	X Y Результат	X Результат
Конъюнктор	Дизъюнктор	Инвертор

Построение логических схем

1. Правило построения логических схем:

2. Определить число логических переменных;

3. Определить количество базовых логических операций и их порядок;

4. Изобразить для каждой логической операции соответствующий ей вентиль;

5. Соединить вентили в порядке выполнения логических операций.

Упражнение 1. Пусть Х = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X V Y & X.

Решение.

1. Две переменные: Х и Y.

2. Две логические операции: V и &.

3. Строим схему:

 

Ответ: 1 V 0 & 1 = 0.

Упражнение 2. Постройте логическую схему, соответствующую логическому выражению F = X & Y V . Вычислить значения выражения для Х=1, Y=0.

Решение.

1. Переменных две: Х и Y.

2. Логических операций три: конъюнкция и две дизъюнкции.

3. Схему строим направо в соответствии с порядком логических операций:

 

 

4. Вычислим значение выражения: F = 1 & 0 V = 0.

Упражнение 3. (самостоятельная работа)

Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения:

1. F = A V B & , если А = 1, В = 1, С = 1 (ответ: 1)

2. F = , если А = 0, В = 1, С = 1 (ответ: 1)

3. F = V B & C, если А = 1, В = 0, С = 1 (ответ: 0)

4. F = (A V B) & (C V B), если А = 0, В = 1, С = 0 (ответ: 1)

Упражнение 4.

Постройте логическое выражение по логической схеме:

А)

 

Ответ: F = A & (B V C).

 

 

Б)

 

Ответ: F = & (( & B) V A).

В)

 

 

Ответ: F = D V A & B & C & ( V ).

Г)

 

 

Ответ: F = (C & ) V .