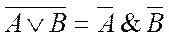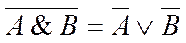Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование функций алгебры логикиСодержание книги Поиск на нашем сайте
Алгебра логики возникла в середине IXX века в трудах Дж. Буля. Первоначально создавалась для решения традиционных логических задач алгебраическими методами. Позднее основными объектами (операндами) алгебры логики стали высказывания и логические операции над ними. Под высказываниями понимаются предложения, относительно которых можно утверждать, истинны они или ложны. Для обозначения и с т и н о с т и вводится символ «И» (true, позднее цифра 1), для обозначения л о ж н о с т и «Л» (false, позднее 0). Обозначение логических операций
& («И») – конъюнкция (логическое умножение) V («ИЛИ», «+») – дизъюнкция (логическое сложение) –> («если то») – импликация, ~ («эквивалентно») – эквивалентность. В качестве операндов в логических выражениях выступают константы или переменные, которые принимают только два значения: «ИСТИНА» (1) или «ЛОЖЬ» (0). Простое логическое выражение – выражение, в котором логические переменные и константы (операнды) связаны знаками логических операций. Логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0) Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных, связанных знаками логических операций. Логические операции и таблицы истинности ОПЕРАЦИЯ ОТРИЦАНИЯ F = не A
Логическое отрицание: ИНВЕРСИЯ -если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным. Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО ОПЕРАЦИЯ ЛОГИЧЕСКОГО УМНОЖЕНИЯ
F = A & B. Логическое умножение КОНЪЮНКЦИЯ – это выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И. ОПЕРАЦИЯ ЛОГИЧЕСКОГО СЛОЖЕНИЯ
F = A + B Логическое сложение – ДИЗЪЮНКЦИЯ – это выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ. Логическое следование: ИМПЛИКАЦИЯ – связывает два простых, второе (В) – следствием из этого условия. результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом "следовательно" и выражается словами ЕСЛИ …, ТО …
ОПЕРАЦИЯ ЭКВИВАЛЕНТНОСТИ F = A~B
Логическая равнозначность: ЭКВИВАЛЕНТНОСТЬ – определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом «эквивалентности» ~. Порядок выполнения логических операций в сложном логическом выражении: 1. инверсия. 2. конъюнкция. 3. дизъюнкция. 4. импликация. 5. эквивалентность. Для изменения указанного порядка выполнения операций используются скобки. Основные законы логики: А = А – закон тождества. А & A Ú
СВОЙСТВА КОНСТАНТ
А Ú 0 = А А & 0 = 0 А Ú 1 = 1 А & 1 = A Законы идемпотентности: А Ú А = А А & А = A Законы коммутативности: А Ú В = В Ú А А & В = В & А Законы ассоциативности: А Ú (В Ú С) = (АÚ В) Ú С А & (В & С) = (А & В) & С Законы дистрибутивности: А Ú (В & С) = (АÚ В) & (А Ú С) А & (В Ú С) = (А & В) Ú (А& С) Законы поглощения: А Ú (А & В) = А А & (А Ú В) = А Законы де Моргана:
В справедливости указанных законов можно убедиться с помощью таблиц истинности Построение таблиц истинности для сложных выражений: Рассчитаем количество строк и столбцов в таблице. Количество строк = 2n + две строки для заголовка (n – количество простых высказываний). Количество столбцов = количество переменных + количество логических операций. При построении таблицы надо учитывать все возможные сочетания логических значений 0 и 1 в исходных выражениях. Затем определить порядок действий и составить таблицу с учетом таблиц истинности основных логических операций. Пример. С оставить таблицу истинности сложного логического выражения D = не A & (B+C). Решение. А, В, С - три простых высказывания, поэтому количество строк = 23 +2 = 10 (n=3, так как на входе три элемента А, В, С) количество столбцов =6: 1) А; 2) В; 3) С; 4) не A это инверсия А (обозначим Е); 5) B + C это операция дизъюнкции (обозначим F); 6) D = не A & (B+C), т.е. D = E & F это операция конъюнкции. Таблица 4.2. Таблица истинности сложного логического выражения
Условное обозначение базовых логических элементов компьютера Логический элемент И конъюнктор
Логический элемент И конъюнктор
Логический элемент ИЛИ дизъюнктор
Логический элемент НЕ Инвертор
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.255.63 (0.007 с.) |

 («не») – отрицание,
(«не») – отрицание, = 1 – закон исключенного третьего (закон означает, что либо высказывание истинно, либо его отрицание должно быть истинным).
= 1 – закон исключенного третьего (закон означает, что либо высказывание истинно, либо его отрицание должно быть истинным).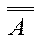 = А – закон двойного отрицания.
= А – закон двойного отрицания. = 1
= 1 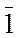 = 0
= 0