Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цифровые автоматы. Логика алгебры.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Системы счисления Дискретное (цифровое) сообщение состоит из набора чисел или символов. Каждое число состоит из цифр. Способ записи чисел цифровыми знаками называется системой счисления. Количество цифр (символов) применяемых в системе называют ее основанием. Минимальный объем информации, который можно записать на носителе информации называют бит. Восемь носителей информации объединили в одну ячейку памяти, и назвали байт. В микроконтроллере данные и промежуточные результаты представлены в двоичной системе счисления. Все регистры памяти в микроконтроллере нумеруются в шестнадцатеричной системе.
Примеры записи чисел в программе: - D’07’ – десятичное число; - B’0111’ – двоичное число; - H’07’или 0х07 или 07h – шестнадцатеричное число. Алгоритм перевода чисел из двоичной системы в шестнадцатеричную систему: сначала двоичное число разбиваем на четверки чисел справа налево, затем для каждой четверки записываем его эквивалент из приведенной таблицы Б1. П р и м е р. 0101 1011 11012 = 5ВD16. Обратный перевод чисел очевиден, необходимо только аккуратно писать именно четверки двоичных чисел, дописывая при необходимости нули слева: 116.= 00012, 216 = 00102. П р и м е р. 415С16=0100 0001 0101 11002. В двоично-десятичной системе каждый десятичный знак отображается четырьмя двоичными числами. Мера информации Первая попытка ввести меру информации была сделана в 1927 г. Р.Хартли(Англия). Естественным требованием, предъявляемым к информа-ционной мере, должно быть требование аддитивности: в двух ячейках должно быть в два раза больше информации, чем в одной. С = log m, где m –число различных состояний системы. Такая мера удовлетворяет требованию аддитивности. Емкость устройства, состоящего из n ячеек, имеющего q = mn состояний, равна емкости одной ячейки, умноженной на число ячеек: C = log mn = n log m За единицу измерения информ.емкости принята двоичная единица, сокращенно bit. C = log 216 = 4 бит, эквивалентно емкости 4 двоичных ячеек. 3 Сигналы. Преобразования сигналов Сигналы разделяются на дискретные и непрерывные как по параметру, так и по времени. Непрерывное сообщение может быть превращено в дискретное. В 1933 г. В.А.Котельниковым сформулирована следующая теорема: «Если функция l (t) не содержит частот выше Fm, Гц, то она полностью определяется своими мгновенными значениями в моменты времени, отстоящие друг от друга на Dt =1/(2 Fm). Интервалы Dt называются интервалами дискретизации. Дискре-тизацией во времени (рисунок 1) называется процесс, когда непрерывное сообщение сводится к сигналу в виде последовательности импульсов, амплитуда которых равна значению исходной функции, передаваемой в дискретные моменты времени k Dt, а интервалы между ними Dt =1/(2 Fm) В свою очередь величина данного аналогового импульса, выраженного в десятичном измерении, соответствующем принятой единице измерения, может быть преобразована в двоичное значение. Например, если величина меряется в амперах, то десятичному значению 10 вольт, будет соответствовать двоичное число 1010.
Рисунок 1- Дискретизация во времени В отличие от изложенного процесс преобразования непрерывной функции в дискретную по параметру (уровню) носит название квантования по параметру. Шагом квантования по параметру называется разность между соседними дискретными значениями функции. Для равномерного квантования шаг квантования D постоянный: Dкв = (lmax - lmin)/(q - 1), где q – число шагов квантования.
Рисунок 2 – Преобразование сигнала методом квантования по уровню с преобразованием в число-импульсный и затем в двоичный код с защитой по четности Дискретизация. Требования по дискретизации при выборках. Дискре-тизацией во времени (рисунок 1) называется процесс, когда непрерывное сообщение сводится к сигналу в виде последовательности импульсов, амплитуда которых равна значению исходной функции, передаваемой в дискретные моменты времени k Dt, а интервалы между ними Dt =1/(2 Fm) В свою очередь величина данного аналогового импульса, выраженного в десятичном измерении, соответствующем принятой единице измерения, может быть преобразована в двоичное значение. Например, если величина меряется в амперах, то десятичному значению 10 вольт, будет соответствовать двоичное число 1010.
Рисунок 1- Дискретизация во времени В отличие от изложенного процесс преобразования непрерывной функции в дискретную по параметру (уровню) носит название квантования по параметру. Шагом квантования по параметру называется разность между соседними дискретными значениями функции. При одновременном введение квантования по времени и по уровню, амплитуда каждой выборки будет принимать ближайшее разрешенное значение из выбранного конечного набора значений. Совокупность всех выборок образует дискретный или цифровой сигнал. Каждое значение дискретного сигнала можно представить числом. В цифровой технике такой процесс называется кодированием, а совокупность полученных чисел- кодом сигнала. Вместо преобразования или передачи конкретных сигналов эти операции в устройствах цифровой техники могут быть выполнены над их кодами. Основы булевой алгебры. Основными понятиями булевой алгебры являются понятия логической переменной и логической функции. Логической переменной называется величина, которая может принимать одно из двух возможных состояний (значений), одно из которых обозначается символом “0”, другое – “1” (для обозначения состояний возможно применение и других символов, например, “Да” и “Нет” и др.). Сами двоичные переменные чаще обозначают символами х 1, х 2,… В силу определения логические переменные можно называть также двоичными переменными. Логической (булевой) функцией (обычное обозначение – у) называется функция двоичных переменных (аргументов), которая также может принимать одно из двух возможных состояний (значений): “0” или “1”. Значение некоторой логической функции n переменных определяется или задается для каждого набора (сочетания) двоичных переменных. Количество возможных различных наборов, которые могут быть составлены из n аргументов, очевидно, равно Законы алгебры логики Основными понятиями булевой алгебры являются понятия логической переменной и логической функции. множество состояний (значений), которые могут принимать как аргументы, так и функции, равно двум. Для этих состояний в булевой алгебре определяются отношение эквивалентности, обозначаемое символом равенства (=) и три операции: а) логического сложения (дизъюнкции), б) логического умножения (конъюнкции), в) логического отрицания (инверсии), обозначаемые соответственно символами: + или
Постулативно полагается, что при выполнении перечисленных операций отношения эквивалентности имеют вид:
На основании постулатов (1) можно вывести следующие соотношения (законы) алгебры логики: 1 Законы одинарных элементов (универсального множества – а), нулевого множества – б), тавтологии – в)):
2 Законы отрицания (двойного отрицания – а), дополнительности – б), двойственности – в)):
Законы абсорбции или поглощения – а) и склеивания – б):
Законы двойственности (3, в), называемые также законами деМоргана, были обобщены К. Шенноном на случай произвольного (n) числа аргументов. Кроме законов, перечисленных выше и не имеющих аналогов в обычной алгебре (алгебре чисел), для алгебры логики справедливы законы обычной алгебры: коммутативные или переместительные, дистрибутивные или распределительные, ассоциативные или сочетательные. Таблицы истинности Любая логическая функция у n двоичных переменных Пример 1. Составить таблицу истинности логической функции у равнозначности (эквивалентности) трех двоичных переменных Решение. Сначала выпишем все возможные наборы (комбинации) трех переменных Для рассматриваемого примера наборы трех переменных нужно перечислить в следующем порядке: 000, 001, 010, 011, 100, 101, 110, 111 – итого восемь двоичных чисел – от 0 до 7. Табл1
Далее для каждого набора двоичных переменных определим, исходя из смысла ситуации, соответствующее значение функции. В результате получаем таблицу истинности логической функции "равнозначность трех двоичных переменных" (табл. 1). Задание логической функции таблицей истинности не всегда удобно. При большом числе двоичных переменных (n ³ 6) табличный способ задания функции становится громоздким и теряет наглядность. Возможен и аналитический способ задания логических функций, который предусматривает запись функции в форме логического выражения, устанавливающего, какие логические операции над аргументами функции должны выполняться и в какой последовательности. 9 Электронный ЛЭ, реализующий функцию “Отрицание” Функция “отрицание” – это функция одного аргумента (другие названия функции: инверсия, логическая связь НЕ). Аналитическая форма задания этой функции: где Электронный ЛЭ, реализующий функцию “Отрицание” в виде определенных уровней электрических сигналов, называют инвертором или ЛЭ “НЕ”. Инвертор на схемах изображается, как показано на рис. 1, а. Вход ЛЭ слева, выход – справа. На выходной линии, в месте соединения ее с прямоугольником, изображается кружок – символ инверсии. На языке цифровой техники инверсия означает, что выходной сигнал (у) противоположен входному (х). Сказанное иллюстрирует рис. 1, б, на котором приведены временные диаграммы инвертора.
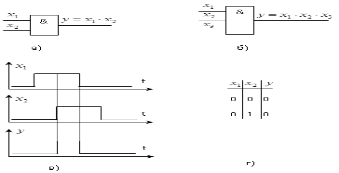
Рисунок 5- Инвертор: а) условное изображение; б) временные диаграммы; в) таблица истинности 10 ЛЭ, реализующий функцию “Конъюнкция” Функция “конъюнкция” – это функция двух или большего числа аргументов (другие названия функции: логическое умножение, логическая связь И). Аналитическая форма задания функции двух аргумент
Функция “конъюнкция” равна 1 тогда и только тогда, когда все ее аргументы равны 1. ЛЭ, реализующий функцию “Конъюнкция” называют конъюнктором или ЛЭ “И”. На рис. 6 приведены: условное графическое изображение двухвходового (а) и трехвходового (б) конъюнкторов; временные диаграммы (в) и таблица истинности (г) двухвходового конъюнктора. ЛЭ “И” часто используют для управления потоком информации. При этом на один из его входов поступают сигналы, несущие некоторую информацию, а на другой – управляющий сигнал: пропустить информацию – 1, не пропустить – 0. ЛЭ “И”, используемый таким образом, называют вентиль.
Рисунок 6 – Конюнкторы 11.Функция “дизъюнкция” – это функция двух или большего числа аргументов (другие названия функции: логическое сложение, логическая связь ИЛИ). Функция равна 1, если хотя бы один из ее аргументов равен 1 (рис. 2, в). Обозначение функции “Дизъюнкция”:
ЛЭ, реализующий функцию “дизъюнкция”, называют дизъюнктором или ЛЭ “ИЛИ”. Условное изображение и временные диаграммы ЛЭ “ИЛИ” приведены на рис. 7
Рисунок 7 – Дизъюнктер или ЛЭ «ИЛИ»
12.Функция “штрих Шеффера” (другое название функции – логическая связь “И-НЕ”) – это функция двух или большего числа аргументов. Таблица истинности функции “И-НЕ” представлена на рис. 8, б. Легко видеть, что это инверсия функции “И”, т.е. отрицание конъюнкции. Функция равна 1, если равен 0 хотя бы один из ее аргументов, функция равна 0 при равенстве всех аргументов 1. Обозначение функции “И-НЕ”: Условное изображение ЛЭ, реализующего функцию “штрих Шеффера”, приведено на рис. 8, а.
Рисунок 8 – ЛЭ «И-НЕ» или функция «штрих Шеффера»
13. Электронно-дырочным называют такой p-n- переход, который образован двумя областями полупроводника с разными типами проводимости: электронной (n) и дырочной (p). Получают p-n- переход с помощью диффузии или эпитаксии. В физике твёрдого тела, ды́рка — это отсутствие электрона в электронной оболочке. Для создания дырок в полупроводниках используется легирование кристаллов акцепторными примесями. Кроме того, дырки могут возникать и в результате внешних воздействий: теплового возбуждения электронов из валентной зоны в зону проводимости, освещения светом или облучения ионизирующим излучением. p-n -перехо́д (n — negative — отрицательный, электронный, p — positive — положительный, дырочный), или электронно-дырочный переход — область пространства на стыке двух полупроводников p- и n-типа, в которой происходит переход от одного типа проводимости к другому. p-n-переход является основой для полупроводниковых диодов, триодов и других электронных элементов с нелинейной вольт-амперной характеристикой.
14. Электронно-дырочная проводимость возникает в результате разрыва валентных связей, являясь собственной проводимостью, которая обычно невелика. Под воздействием электрического поля, температуры и других внешних факторов электрические свойства полупроводников изменяются в значительно большей степени, чем свойства проводников и диэлектриков. Для увеличения электропроводности в полупроводники вводят незначительное количество примесей, при этом оказывается, что в зависимости от рода примеси получают как полупроводники с дырочной проводимостью (при добавках трёхвалентной примеси — акцепторов типа индий (In)), называемых полупроводниками p -типа, так и полупроводники с электронной проводимостью (при добавках пятивалентной примеси — доноров типа мышьяк (As)), называемых полупроводниками n -типа. При сплавлении полупроводников различных типов создаётся область объёмного заряда по обе стороны от границы раздела, называемая электронно-дырочным или p-n -переходом.
15. Электронно-дырочный переход — область пространства на стыке двух полупроводников p- и n-типа, в которой происходит переход от одного типа проводимости к другому. p-n-переход является основой для полупроводниковых диодов, триодов и других электронных элементов с нелинейной вольт-амперной характеристикой
Рисунок 38 - Энергетическая диаграмма p-n -перехода. a) Состояние равновесия b) При приложенном прямом напряжении c) При приложенном обратном напряжении В полупроводнике p-типа концентрация дырок намного превышает концентрацию электронов. В полупроводнике n-типа концентрация электронов намного превышает концентрацию дырок. Если между двумя такими полупроводниками установить контакт, то возникнет диффузионный ток — носители заряда, хаотично двигаясь, перетекают из той области, где их больше, в ту область, где их меньше. При такой диффузии электроны и дырки переносят с собой заряд. Как следствие, область на границе станет заряженной, и область в полупроводнике p-типа, которая примыкает к границе раздела, получит дополнительный отрицательный заряд, приносимый электронами, а пограничная область в полупроводнике n-типа получит положительный заряд, приносимый дырками.
16. В полупроводнике p-типа концентрация дырок намного превышает концентрацию электронов. В полупроводнике n-типа концентрация электронов намного превышает концентрацию дырок. Если между двумя такими полупроводниками установить контакт, то возникнет диффузионный ток — носители заряда, хаотично двигаясь, перетекают из той области, где их больше, в ту область, где их меньше. При такой диффузии электроны и дырки переносят с собой заряд. Как следствие, область на границе станет заряженной, и область в полупроводнике p-типа, которая примыкает к границе раздела, получит дополнительный отрицательный заряд, приносимый электронами, а пограничная область в полупроводнике n-типа получит положительный заряд, приносимый дырками. Таким образом, граница раздела будет окружена двумя областями пространственного заряда противоположного знака. Электрическое поле, возникающее вследствие образования областей пространственного заряда, вызывает дрейфовый ток в направлении, противоположном диффузионному току. В конце концов, между диффузионным и дрейфовым токами устанавливается динамическое равновесие и перетекание зарядов прекращается.
17. Электрическое поле, возникающее вследствие образования областей пространственного заряда, вызывает дрейфовый ток в направлении, противоположном диффузионному току. В конце концов, между диффузионным и дрейфовым токами устанавливается динамическое равновесие и перетекание зарядов прекращается. При этом возникает так называемый запирающий (барьерный) слой в несколько микрометров, лишенный носителей заряда, с напряженностью Eз электрического поля, которая препятствует диффузии носителей заряда (рис. 10, а).
Рисунок 10 – Запирающий слой: а) при отсутствии напряжения; б)при подаче обратного напряжения; в)при подаче прямого напряжения
18. Полупроводниковым диодом называют прибор с одним p-n- переходом, имеющим два вывода: анод А и катод К.
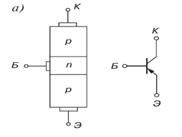
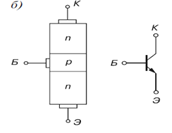
Рисунок 11- ВАХ диода 19. Транзистор — это полупроводниковый прибор, предназначенный для усиления, инвертирования, преобразования электрических сигналов, а также переключения электрических импульсов в электронных цепях различных устройств. Различают биполярные транзисторы, в которых используются кристаллы n- и p- типа, и полевые (униполярные) транзисторы, изготовленные на кристалле германия или кремния с одним типом проводимости. Биполярные транзисторы — это полупроводниковые приборы, выполненные на кристаллах со структурой p-n-p- типа (а) или n-p-n -типа (б) с тремя выводами, связанными с тремя слоями (областями): коллектор (К), база (Б) и эмиттер (Э) (рис. 20).
Рисунок 20- Биполярные транзисторы: а)структура p-n-p- типа; б)структура n-p-n -типа
20. Триггер - это устройство последовательного типа с двумя устойчивыми состояниями равновесия, предназначенное для записи и хранения информации. Под действием входных сигналов триггер может переключаться из одного устойчивого состояния в другое. При этом напряжение на его выходе скачкообразно изменяется. Как правило, триггер имеет два выхода: прямой и инверсный. Число входов зависит от структуры и функций, выполняемых триггером. По способу записи информации триггеры делят на асинхронные и синхронизируемые (тактируемые). В асинхронных триггерах информация может записываться непрерывно и определяется информационными сигналами, действующими на входах в данный момент времени. Если информация заносится в триггер только в момент действия так называемого синхронизирующего сигнала, то такой триггер называют синхронизируемым или тактируемым. Помимо информационных входов тактируемые триггеры имеют тактовый вход вход синхронизации. В цифровой технике приняты следующие обозначения входов триггеров: S - раздельный вход установки в единичное состояние (напряжение высокого уровня на прямом выходе Q);
Разновидности диодов В зависимости от назначения и свойств различают выпрямительные диоды, стабилитроны, высокочастотные диоды, импульсные диоды, варикапы, диоды Шоттки, светодиоды, фотодиоды, диодные оптроны и т. п. Выпрямительные диоды используют в схемах преобразования (выпрямления) переменного тока в постоянный ток. Как правило, это плоскостные диоды средней и большой мощности. В высокочастотных и импульсных маломощных цепях электронных устройств используют точечные диоды: кремниевые типа КД или 2Д и германиевые типа ГД или 1Д, из арсенида галлия типа 3Д. Например, диоды ГД107А, КД203Д рассеивают мощность Р от 1 до 1,5 Вт, а диод КД512А — мощность P > 1,5 Вт. К маломощным относят диоды с мощностью рассеивания до 0,3 Вт, к диодам средней мощности от 0,3 до 10 Вт, диоды большой мощности с мощностью рассеяния P>10 Вт. Основные параметры выпрямительных диодов: Iпр - прямой ток; Uпр — прямое напряжение; Iпрmax - максимальный допустимый прямой ток; Uобр.mах — максимальное допустимое обратное напряжение; Iобр - обратный ток, который нормируется при определенном обратном напряжении. В настоящее время выпускаются так называемые диодные столбы, в которых для увеличения обратного напряжения последовательно соединены от 5 до 50 диодов с допустимым обратным напряжением от 2 до 40 кВ.
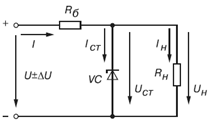
ВАХ стабилитрона Стабилитроны или опорные кремниевые диоды предназначены для использования в параметрических стабилизаторах напряжения (рис. 13). Рабочим участком ВАХ стабилитрона является участок обратной её ветви, соответствующий области обратного электрического пробоя p-n- перехода (рис. 13) и ограниченный минимальным и максимальным значениями тока.
Рисунок 13 Схема включения стабилитрона и его ВАХ
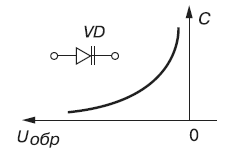
При работе в этой области обратное напряжение на стабилитроне Uобр незначительно изменяется при относительно больших изменениях тока ВАХ Варикапа Варикапы — это полупроводниковые диоды, предназначенные для использования их ёмкости, управляемой обратным напряжением Uобр (рис. 14).
Рисунок 14- ВАХ варикапа
24. ВАХ диода Шотки Диоды Шоттки — это полупроводниковые приборы, в которых используются свойства потенциального барьера (барьера Шоттки) на контакте металл — полупроводник.В рассматриваемых диодах из-за разной высоты потенциальных барьеров для электронов и дырок нет инжекции неосновных носителей заряда, нет и таких медленных процессов, как накопление и рассасывание неосновных носителей в базе. В результате инерционность диодов с выпрямлением на контакте металл —полупроводник определяется величиной барьерной ёмкости выпрямляющего контакта (Cбар = 1 пФ). Кроме того, у этих диодовнезначительные активные потери (прямое напряжение Uпр = 0,4 В,что на 0,2 В меньше, чем у обычных диодов). ВАХ диодов Шоттки — строгая экспонента (рис. 15).
Рисунок 15-ВАХ диода Шотки
ВАХ светодиода Светодиоды — это излучающие полупроводниковые приборы (индикаторы), предназначенные для непосредственного преобразования электрической энергии в энергию некогерентного светового излучения. В основе принципа функционирования светодиодов лежит преобразование электрической энергии в электромагнитное излучение, спектр которого полностью или частично лежит в видимой области, диапазон длин волн которой составляет 0,45-0,68 мкм.
Рисунок 17-ВАХ светодиода
ВАХ фотодиода Фотодиод — это полупроводниковый прибор с p-n- переходом, обратный ток которого зависит от освещенности Ф (рис. 18, а).
27. Биполярные транзисторы Биполярные транзисторы — это полупроводниковые приборы, выполненные на кристаллах со структурой p-n-p- типа (а) или n-p-n -типа (б) с тремя выводами, связанными с тремя слоями (областями): коллектор (К), база (Б) и эмиттер (Э) (рис. 20).
Рисунок 20- Биполярные транзисторы: а)структура p-n-p- типа; б)структура n-p-n -типа
База Б — это средний тонкий слой, служащий для смещения эмиттерного и коллекторного переходов. Толщина базы должна быть меньше длины свободного пробега носителей заряда. Эмиттер Э — наружный слой, источник носителей заряда с высокой концентрацией носителей, значительно большей, чем в базе. Второй наружный слой К, принимающий носителей заряда, называют коллектором. Ток в таком транзисторе определяется движением зарядов двух типов: электронов и дырок. Отсюда его название — биполярный транзистор.
28. Три режима работы транзистора Каждый из переходов транзистора — эмиттерный (Б-Э) и коллекторный (Б-К) можно включить либо в прямом, либо в обратном направлении. В зависимости от этого различают три режима работы транзистора: - режим отсечки — оба p-n- перехода закрыты, при этом через транзистор протекает сравнительно небольшой ток I 0, обусловленный неосновными носителями зарядов; - режим насыщения — оба p-n -перехода открыты; - активный режим — один из p-n -переходов открыт, а другой закрыт. В режимах отсечки и насыщения управление транзистором практически отсутствует. В активном режиме транзистор выполняет функцию активного элемента электрических схем усиления сигналов, генерирования колебаний, переключения и т. п.
29. Нормальное и инверсное включение транзистора Если на эмиттерном переходе напряжение прямое, а на коллекторном обратное, то такое включение транзистора считают нормальным, при противоположной полярности напряжений — инверсным. Полевой транзистор Транзистор — это полупроводниковый прибор, предназначенный для усиления, инвертирования, преобразования электрических сигналов, а также переключения электрических импульсов в электронных цепях различных устройств. Различают биполярные транзисторы, в которых используются кристаллы n- и p- типа, и полевые (униполярные) транзисторы, изготовленные на кристалле германия или кремния с одним типом проводимости. Полевой транзистор — это полупроводниковый прибор, в котором ток стока (С) через полупроводниковый канал п- или р -типа управляется электрическим полем, возникающим при приложении напряжения между затвором (З) и истоком (И). Полевые транзисторы изготавливают: - с управляющим затвором типа p-n-перехода для использования в высокочастотных (до 12_18 ГГц) преобразовательных устройствах. Условное их обозначение на схемах приведено на рис. 24, а, б; - с изолированным (слоем диэлектрика) затвором для использования в устройствах, работающих с частотой до 1_2 ГГц. Их изготавливают или со встроенным каналом в виде МДП_структуры (см. их условное обозначение на рис. 24, в и г), или с индуцированным каналом в виде МОП_структуры (см. их условное обозначение на рис. 24, д, е).
Рисунок 24-Виды полевых транзисторов
Обозначение входов триггера Помимо информационных входов тактируемые триггеры имеют тактовый вход вход синхронизации. В цифровой технике приняты следующие обозначения входов триггеров: S - раздельный вход установки в единичное состояние (напряжение высокого уровня на прямом выходе Q); Наибольшее распространение в цифровых устройствах получили RS-триггер с двумя установочными входами, тактируемый D-триггер и счетный Т-триггер. Рассмотрим функциональные возможности каждого из них.
Асинхронный RS-триггер Асинхронный RS-триггер. В зависимости от логической структуры различают RS-триггеры с прямыми и инверсными входами. Их схемы и условные обозначения приведены на рисунке. Триггеры такого типа построены на двух логических элементах 2ИЛИ-НЕ - триггер с прямыми входами (А), 2И-НЕ - триггер с инверсными входами (Б).
Рисунок 27-Асинхронный RS-триггер
Тактируемый D-триггер. Он имеет информационный выход и вход синхронизации. Одна из возможных структурных схем однотактного D-триггера и его условное обозначение показаны на рисунке 28.
Рисунок 28-тактируемый D-триггер Если уровень сигнала на входе C= 0, состояние триггера устойчиво и не зависит от уровня сигнала на информационном входе. При этом на входы RS-триггера с инверсными входами (элементы 3 и 4) поступают пассивные уровни (-S=-R=1). При подаче на вход синхронизации уровня С=1 информация на прямом выходе будет повторять информацию, подаваемую на вход D. Таким образом, при C=0 Qt+1=Qt, C=1 Qt+1=D. Таблица истинности тактируемого D-триггера имеет вид:
Счетный Т-триггер T-триггер — это счетный триггер. У данного триггера имеется только один вход. Принцип работы T-триггера заключается в следующем. После поступления на вход T импульса, состояние триггера меняется на прямо противоположное. Счётным он называется потому, что T триггер как бы подсчитывает количество импульсов, поступивших на его вход. Жаль только, что считать этот триггер умеет только до одного. При поступлении второго импульса T-триггер снова сбрасывается в исходное состояние. T-триггеры строятся только на базе двухступенчатых триггеров, подобных рассмотренному ранее D триггеру. Использование двух триггеров позволяет избежать неопределенного состояния схемы при разрешающем потенциале на входе синхронизации "C", так как счетные триггеры строятся при помощи схем с обратной связью T триггер можно синтезировать из любого двухступенчатого триггера. Рассмотрим пример синтеза T триггера из динамического D триггера. Для того чтобы превратить D триггер в счётный, необходимо ввести цепь обратной связи с инверсного выхода этого триггера на вход, как показано на рисунке 1.
Временная диаграмма T триггера приведена на рисунке 31. При построении этой временной диаграммы был использован триггер, работающий по заднему фронту синхронизирующего сигнала.
Т-триггеры используются при построении схем различных счётчиков, поэтому в составе БИС различного назначения обычно есть готовые модули этих триггеров.
Общие принципы фон Неймана В основу построения подавляющего большинства компьютеров положены следующие общие принципы, сформулированные в 1945 г. американским ученым Джоном фон Нейманом. Принцип программного управления. Программа состоит из набора команд, выполняющихся процессором автоматически в определенной последовательности. Принцип однородности памяти. Программы и данные хранятся в одной и той же памяти, поэтому компьютер не различает, что хранится в данной ячейке памяти — число, текст или команда. Над командами можно выполнять такие же действия, как и над данными.
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.78.249 (0.012 с.) |





 . При этом, поскольку сама функция на каждом наборе может принимать значение “0” или “1”, то общее число возможных функций от n переменных равно
. При этом, поскольку сама функция на каждом наборе может принимать значение “0” или “1”, то общее число возможных функций от n переменных равно  .
. - операция дизъюнкции,
- операция дизъюнкции, или
или  или & - операция конъюнкции,
или & - операция конъюнкции, - операция инверсии (* - символ аргумента или функции).
- операция инверсии (* - символ аргумента или функции).



 может быть задана таблично. Такие таблицы, получившие название таблиц истинности, содержат
может быть задана таблично. Такие таблицы, получившие название таблиц истинности, содержат  , т.е. функции, которая принимает единичное значение только при совпадении всех трех аргументов, ее образующих.
, т.е. функции, которая принимает единичное значение только при совпадении всех трех аргументов, ее образующих.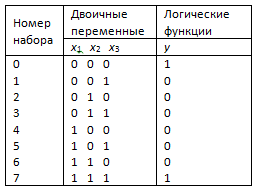

 - логическая функция,
- логическая функция,  - аргумент.
- аргумент.
 и
и  :
: или
или  или
или  .
.
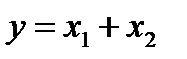 или
или  .
.
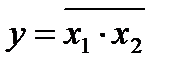 .
.