
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика вивчення ділення багатоцифрових чисел на двоцифрове числоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Випадки ділення на круглі числа. Прийом ділення на круглі числа полягає у поданні круглого числа у вигляді добутку числа і розрядної одиниці і послідовному діленні кожного неповного діленого спочатку на розрядну одиницю, а потім на число. Тому на етапі актуалізації слід повторити усний усного послідовного ділення чисел, що закінчуються нулями, наприклад: 900: 30 = 900: (10 * 3) = 900: 10: 3 = 90: 3 = 30 180: 60 = 180: (10 * 6) = 180: 10: 6 = 18: 6 = 3 5600: 800 = 5600: (100 * 8) = 5600: 100: 8 = 56: 8 = 7 Ознайомлення з письмовим діленням на круглі числа пропонуємо здійснити на прикладі ділення трицифрового числа на кругле число, а потім перенести новий спосіб дії на випадки ділення багатоцифрових чисел на круглі десятки або круглі сотні.
Так нераціонально визначати перше неповне ділене, тому що очевидно що число сотень не можна поділити на двоцифрове число, так щоб отримати хоч би одну сотню. Тому відразу треба в діленому ліворуч відділити дві цифри, і починати міркувати саме з числа десятків: 78 десятків можна поділити на 30 так, щоб отримати хоч би один десяток, тому 78 десятків – це перше неповне ділене. Найвищий розряд частки – десятки, тому в частці буде дві цифри. Ділимо 78 десятків на 30. Для цього число 30 подаю у вигляді добутку розрядної одиниці 10 та числа 3. Послідовно ділю: 78: 10 приблизно буде 7 (щоб поділити число на 10, достатньо справа прикрити в числі одну цифру), 7: 3 приблизно буде 2. Пишу в частці на місці десятків цифру 2. Дізнаємося дією множення скільки десятків розділилося. 60 десятків розділилося. Дізнаємось дією віднімання скільки десятків не розділилося. 18 десятків не розділилося. Перевіряємо чи вірно знайдена цифра частки: остача 18 менша за дільник 30. Цифру частки знайдено вірно. Утворюємо друге неповне ділене: 18 десятків – це 180 одиниць; 180 одиниць – друге неповне ділене. Ділимо 180 одиниць на 30 послідовно: 180: 10 = 18, 18: 3 = 6. Пишімо цифру 6 у частці на місці одиниць. Дією множення дізнаємось скільки одиниць розділилося. Розділилося 180 одиниць. Усі одиниці розділилися. Ділення закінчено. Пропонуємо учням порівняти наступну частку чисел з попередньою і встановити чи можна так само міркувати при діленні на кругле число, як і у попередньому випадку?
Аналогічно виконується ділення на круглі сотні і круглі тисячі.
Ділення багатоцифрового числа на двоцифрове. Спочатку доцільно опрацювати прийом письмового ділення на двоцифрове число на прикладі письмового ділення трицифрового числа на двоцифрове. Першим випадком письмового ділення на двоцифрове число є випадок ділення трицифрового числа на двоцифрове число, коли в частці лише одна цифра. При вивченні цього матеріалу корисно згадати спосіб підбору, що застосовувався при усному діленні двоцифрового числа на двоцифрове: - Число 51 поділити на 17 – це означає знайти таке число, яке при множенні на 17 дає 51:
- Міркуємо так: знаходимо таке число, яке при множенні на одиниці дільника - 7, дає число, яке закінчується одиницями діленого – 1; це число 3, більше таких чисел немає.
3 * 7 = 21 3 * 17 = 51, 51 = 51 - Таким чином, 51 поділити на 17 в частці отримаємо 3, тому що 3 помножити на 17 дає 51. Аналогічно міркуємо при знаходженні значень часток: 91: 13 57: 19 98: 14 95: 19 72: 36 60: 12 - Порівняйте всі ці приклади. Що в них спільного? (Спільним є те, що в усіх випадках ділили на двоцифрове число, а також в усіх випадках в частці отримали одноцифрове число. Також в усіх випадках є спільним спосіб обчислення.) - Чому в усіх випадках в частці отримали лише одну цифру? (В частці лише одна цифра, тому що число десятків кожного діленого не можна поділити на дільник, так щоб отримати в частці десятки, тому першим неповним діленим буде все число одиниць, тому в частці отримаємо одиниці, а значить лише одну цифру.) - Запишіть вираз: “ ділене число 224, дільник –32.”. Скільки цифр буде в частці? (У дільнику дві цифри, тому в діленому відділяємо зліва також дві цифри, маємо 22 десятки. 22 десятки не можна поділити на 32, так щоб отримати хоч би 1 десяток, тому переходимо до наступного розряду одиниць. В діленому всього 224 одиниці. Тому першим неповним діленим буде 224 одиниці. Значить найвищій розряд частки – одиниці. Щоб записати одиниці потрібна лише одна цифра.) - Порівняйте цей випадок ділення з попередніми. Чим вони схожі? (Схожі тим, що тут також ділимо на двоцифрове число і в частці отримаємо лише одну цифру.) А чим вони відрізняються? (Відрізняються діленими: в цьому випадку ділене є трицифровим числом.) - Чи можна при розв’язуванні міркувати так само, як і в попередніх випадках. Спробуємо: число 224 поділити на 32 – це означає знайти таке число, яке при множенні на 32 дає 224. Прикинемо які числа слід випробувати множенням: знайдемо таке число, яке при множенні на одиниці дільника – 2, дає число,що закінчується одиницями діленого – 4; це числа 2, та 7. Лише ці числа будемо випробувати множенням.
2 * 2 = 4 2 * 32 = 64, 64 = 224 7 * 2 = 14 7 * 32 = 224, 224=224 - З якими труднощами ми зустрілися при розв’язуванні цього прикладу? (Важко було усно множити 7 на 32, тому що в добутку отримуємо трицифрове число.) - Розв’язок можна записати інакше – куточком:
22 4 3 2 224 7 2, 7 -? 0. -
- Визначимо найвищій розряд частки та кількість цифр в частці. (Перше неповне ділене 425 одиниць, тому в частці отримаємо одиниці в найвищому розряді, значить в частці буде лише 1 цифра; поставимо одну крапку на місці цифр частки.) - Як треба міркувати при визначенні частки? (Треба прикинути: знайти такі числа, які при множенні на одиниці дільника – 5 дають числа, які закінчуються на одиниці діленого – 5. Це такі числа: 3, 5,7, 9. Випробуємо їх множенням 3 * 85 =255, не отримали ділене. Випробуємо 5: 5 * 85 = 425, отримали ділене. Тому в частці 5.)
- Випробувати декількох чисел множенням дійсно незручно, довго. Тому, будемо прикидати, яке саме з обраних чисел слід випробувати множенням. Розглянемо приклад:
468 52 . 4, 9 -? - Для того,щоб прикинути, яке з двох чисел є часткою, замінимо дільник меншим круглим числом:
468 52 50 . 4, 9 -? - Як розділити на кругле число? (Число 50 треба подати у вигляді добутку розрядної одиниці і числа: 10 та 5; і послідовно розділити спочатку на розрядну одиницю, а потім результат поділити на число.)
468 52 50 = 10 * 5 . 4, 9 -? - Таким чином, 468 спочатку поділимо на 10, а потім на 5. (468: 10 - Тому будемо множити число 9 на 52. Записуємо відразу цифру 9 в частці і виконуємо множення.
468 52 50 = 10 * 5; 468: 10 468 9 4, 9 -? 0. Замінюючи дільник ближчим меншим круглим числом, обчисліть значення часток: 150: 75 406: 58 195: 65 464: 58.
Далі учні знайомляться з випадками ділення трицифрового числа на двоцифрове, коли в частці дві цифри. До цього моменту учні вже знають алгоритм письмового ділення на одноцифрове число, вміють прикидати цифри частки способом заміни дільника меншим круглим числом, та поступовим діленням діленого спочатку на 10, а потім на число. Тому ці уміння слід актуалізувати і перенести в нову ситуацію: - Знайдіть значення частки чисел 828 та 36. (Записуємо числа куточком. Визначаємо перше неповне ділене: в дільнику 2 цифри, тому в діленому відділяємо ліворуч також дві цифри – отримуємо 82 десятки; 82 десятка можна поділити на 36, так щоб отримати десятки. Таким чином перше неповне ділене 82 десятка. Тому, в частці найвищій розряд буде десятки, а значить дві цифри.) 82 8 36
..
- Як треба міркувати, щоб 82 десятки поділити на 36? Що можна зробити, щоб прикинути, яка цифра буде першою цифрою частки? (Треба дільник 36 замінити меншим круглим число 30. Число 30 можна подати у вигляді добутку 10 та 3. Перше неповне ділене 82 поділимо спочатку на 10, а потім на 2. 82: 10
82 8 36 30 = 10 * 3 2 82: 10 .. - Як дізнатися скільки десятків поділилося? (Щоб дізнатися, скільки десятків поділилося, треба 2 помножити на 36. 72 десятки розділилися.) - Як дізнатися скільки десятків не розділилися? (Треба від першого неповного діленого 82 десятків відняти 72 десятки. 10 десятків не розділилися.) - Як перевірити, чи вірно знайдена цифра частки? (Порівнюємо остачу з дільником: 10 менше 36 – остача меша за дільник.)
82 8 36 30 = 10 * 3 72 2 82: 10 10 .. - Як треба міркувати, щоб утворити друге неповне ділене? (Залишилося 10 десятків – це 100 одиниць, та в діленому є 8 одиниць; таким чином 108 одиниць – друге неповне ділене.)
82 8 36 30 = 10 * 3 72 2 82: 10 108 ..
- Як визначити другу цифру частки? (Треба 108 спочатку поділити на 10, а потім поділити на 3. 108: 10 82 8 36 30 = 10 * 3 72 23 82: 10 108 .. 108: 10 - Дізнайтеся, скільки одиниць розділилося? (Розділилося 108 одиниць.) Скільки одиниць не розділилося? (Всі одиниці розділилися, ділення закінчено.)
82 8 36 30 = 10 * 3 72 23 82: 10 108 .. 108: 10 108 Закріплення здійснюється під час розв’язання прикладів: 768: 32 494: 38 546: 21 552: 24. Не завжди отримана таким чином цифра частки підходить, іноді при множенні знайденої цифри частки на дільник отримуємо більше число за неповне ділене. Тому слід познайомити учнів із способом перевірки пробних цифр частки. Ділене 952, дільник 34. Знайдемо частку. (Записуємо ділене і дільник. Відділяємо дільник куточком. Визначаємо перше неповне ділене, для цього в дільнику підраховуємо кількість цифр – 2 цифри, тому в числі 952, ліворуч відділяємо також 2 цифри; отримуємо 95 десятків. 95 десятків можна поділити на 34 так, щоб отримати десятки, тому 95 десятків є першим неповним діленим. Так яка 95 десятків перше неповне ділене, то в частці отримуємо найвищій розряд десятки, а значить 2 цифри; ставимо дві крапки на місці цифр частки. Знаходимо першу цифру частки, для цього 34 замінимо ближчим круглим числом – 30. 30 це 10 помножене на 3. Таким чином, 95 поділимо спочатку на 10, а потім на 3. 95: 10
95 2 34 30 = 10 * 3 102 3 95: 10 .. - Що цікавого ви помітили? Чи можна від 95 відняти 102? (Ми не можемо від меншого числа відняти більше.) В чому полягає проблема? (У нас лише 95 десятків, але виходить, що поділилося 102 десятки, що не можливо.) Про що це свідчить? (Це свідчить про те, що цифра десятків частки знайдена невірно.) - Так, не завжди міркуючи способом заміни дільника меншим круглим числом, ми отримуємо вірну цифру частки. Отримані цифри треба перевіряти. - Таким чином, цифра 3 – це пробна цифра, її треба перевірити. Можна перевірити множенням, як ми і зробили зараз, а можна прикинути. Як ви вже впевнилися прикидати легше, ніж обчислювати. Тому будемо прикидати. - При перевірці пробних цифр частки прикидають так: отримане число множать на десятки дільника – 3 * 30 = 90. Визначають, що залишиться від неповного діленого, після цього: 95 – 90 = 5. Порівнюють остачу з добутком пробного числа 3 на одиниці дільника 4. Очевидно, що 5 < 3 * 4 – 5 не вистачить, щоб 3 помножити на 4. Тому цифра 3 не підходить, треба взяти на одиницю менше – 2. Перевіримо цифру 2. Для цього 2 множимо на десятки діленого: 2 * 30 = 60. Визначаємо, скільки лишається від неповного діленого: 95 – 60 = 35. Порівнюємо остачу 35 з добутком 2 на число одиниць 4: 35 > 2 * 4 – 35 вистачить, щоб 2 помножити на 4. Тому цифра 2 підходить, пишімо її в частці.
95 2 34 30 = 10 * 3 68 2 95: 10 27 .. 95 – 90 = 5 5 < 3 * 4 2 -? 2 * 30 = 60 95 – 60 = 35 35 > 2 * 4
- Скільки десятків розділилося? (Розділилося 68 десятків.) Скільки десятків не розділилося? (Не розділилося 27 десятків.) Перевірте, остачу. (Остача меша за дільник, тому ділення виконане вірно.) - Утворіть друге неповне ділене. (Залишилося 27 десятків – це 270 одиниць, та ще 2 одиниці діленого, буде 272 одиниці – друге неповне ділене.) - Знайдіть другу цифру частки. (272 поділимо спочатку на 10, а потім на 3. 272: 10 - Перевіримо цю цифру. Що для цього треба зробити? (Треба помножити її на десятки дільника: 9 * 30 = 270. Визначити, скільки залишиться від неповного діленого: 272 – 270 = 2. Порівняти остачу 2 з добутком пробної цифри 9 на одиниці діленого: 2 < 9 * 4, двох не вистачить щоб 9*4, тому цифра 9 не підходить. Візьмемо на одиницю менше – 8. Перевіримо її. Помножимо 8 на десятки дільника: 8 * 30 = 240. Визначимо, скільки залишиться від неповного діленого: 272 – 240 = 32. Порівнюємо остачу 32 з добутком пробної цифри 8 на одиниці дільника 4: 32 = 8 * 4, 32 вистачить, щоб 8 * 4, тому цифра 8 є цифрою частки; запишімо її на другому місці. 95 2 34 30 = 10 * 3 68 28 95: 10 272 .. 95 – 90 = 5 272 5 < 3 * 4 0 2 -? 2 * 30 = 60 95 – 60 = 35 35 > 2 * 4 272: 10 272 – 270 = 2 2 < 9 * 4 8 -? 8 * 30 = 240 272 – 240 = 32 32 = 8 * 4
- Дізнайтеся, скільки одиниць розділилося. (Розділилося 272 одиниці.) Скільки одиниць не розділилося? (Всі одиниці розділилися, ділення закінчено.)
З метою закріплення способу перевірки пробних цифр частки учням пропонується виконати ділення письмово: 912: 24 546: 26 912: 24 828: 36 925: 37. Далі діти виконують письмове ділення трицифрового числа на двоцифрове з остачею. Міркування здійснюються за відомим алгоритмом, але не відміну від ділення націло, не усі одиниці діленого розділяться, тому слід ще раз остачу порівняти з дільником і зробити висновок про вірність знайденої цифри частки.
Ділення багатоцифрового числа на двоцифрове число. Міркування здійснюється за відомою пам’яткою ділення на двоцифрове число. 31595 71 284 445 4 -? 4 -? 5 -? 319 4 * 70 = 280 4 * 70 = 280 5 * 70 = 350 284 315 – 280 = 35 319 – 280 = 39 355 – 350 = 5 355 35 > 4 * 1 39 > 4 * 1 5 = 5 * 1 355 Міркування. В дільнику дві цифри, тому в діленому відділяю ліворуч дві цифри: 31 тисяча. 31 тисячу не можна поділити на 71, щоб отримати хоч-би одну тисячу. Тому переходжу до наступного розряду. 315 сотень – перше неповне ділене. Оскільки перше неповне ділене сотні, то в частці в найвищому розряд теж будуть сотні, тому в частці буде три цифри. Ділю перше неповне ділене на дільник: 315: 71 Дізнаюся скільки сотень розділилося дією множення. 284 сотні розділилося. Дізнаюся скільки сотень не розділилося дією віднімання.31 сотня не розділилася. Перевіряю остачу: остача 31 менша за дільник 71; тому цифру частки підібрано вірно. Утворюю друге неповне ділене: 31 сотня – це 310 десятків і в діленому 9 десятків, тому 319 десятків – друге неповне ділене. Ділю його на 71, приблизно буде по 4. 4 – це пробна цифра, її слід перевірити: 4 множимо на десятки дільника (4 * 70), буде 280; віднімаю отримане число з неповного діленого (319 – 280), буде 39; порівнюю остачу з добутком пробної цифри на дільник (4 * 1); остача більша, тому пробна цифра підходить, пишу її на місці десятків в частці. Дізнаюся скільки десятків розділилося дією множення. 284 десятки розділилися. Дізнаюся скільки десятків не розділилося дією віднімання. 35 десятків не розділилося. Перевіряю остачу: остача 35 менша за дільник 71; тому цифру частки підібрано вірно. Утворюю третє неповне ділене: 35 десятків – це 350 одиниць і ще 5 одиниць в діленому. 355 одиниць – третє неповне ділене. Ділю його на 71, приблизно буде по 5. 5 – це пробна цифра, її слід перевірити: 5 множимо на десятки дільника (5 * 70), буде 350; віднімаю отримане число з неповного діленого (355 – 350), буде 5; порівнюю остачу з добутком пробної цифри на дільник (5 * 1); остача дорівнює добутку, тому пробна цифра підходить, пишу її на місці одиниць в частці. Дізнаюся скільки одиниць розділилося дією множення. 355 одиниць розділилися. Дізнаюся скільки одиниць не розділилося дією віднімання. Усі одиниці розділилися, ділення закінчено.
Далі вивчаються випадки ділення п’яти - шестицифрових чисел, які закінчуються нулями. Учні вже знайомі з випадками ділення круглих чисел на одноцифрові, і вміють пояснювати чому на місці одиниць треба записати нуль. Ці знання треба актуалізувати на етапі підготовчої роботи і перенести в нову ситуацію. Отже учні можуть самостійно виконати ділення поданих чисел і пояснити чому саме на місці одиниць буде нуль.
Ділю 334 на 75: 334: 75 300 тисяч розділилося, 34 тисячі не розділилися. Остача 34 менша за дільник, тому цифру частки знайдено вірно.
З остачі 34 тисячі та 5 сотень діленого утворюю друге неповне ділене – 345 сотень. 345: 75 300 сотень розділилося. 45 сотень не розділилося. Остача 45 менша за дільник, тому цифру частки знайдено вірно. 45 сотень – це 450 десятків, у діленому 0 десятків, тому третє неповне ділене 450 десятків. 450: 75 450 десятків розділилося. Усі десятки розділилися, тому в частці ми отримали 446 десятків – це 4460 одиниць. Або міркувати можна ще й так: Четверте неповне ділене 0 одиниць. 0: 75 = 0 – пишімо нуль на місці одиниць у частці. Ділення закінчено.
Наступний випадок ділення багатоцифрових чисел на двоцифрові, коли в середині частки є нуль. Знову, треба звернутися до аналогічних випадків ділення на одноцифрове число і перенести відомий дітям спосіб міркування в нову ситуацію.
Ділю 450 на 74, 45: 7 Розділилося 444 сотні. Не розділилося 6 сотень.
Перевіряю: остача 6 менша за дільник 74, цифру частки знайдено вірно. З остачі 6 сотень та 6 десятків, утворюю друге неповне ділене – 66 десятків. 66 десятків не можна розділити на 74, щоб отримати хоч би один десяток, тому на місці десятків у частці пишу цифру 0. Або 66: 74 = 0 (ост. 66). 0 десятків розділилося. 66 десятків не розділилося. Утворюю третє неповне ділене з остачі та одиниць діленого – 666 одиниць. Ділю 666 на 74: 66: 7 9 * 70 = 630, 666 – 630 = 36, 36 = 9 * 4, - цифра 9 підходить, пишу її на місці одиниць у частці. Розділилися усі одиниці. Ділення закінчено. Розглядаючи короткий запис таких випадків письмового ділення, треба звернути увагу на те, що при множенні дільника 35 на нуль завжди отримуємо нуль, а при відніманні нуля з неповного діленого 14 десятків, буде те ж саме число – 14 десятків; тому тут нуль не пишуть, але запам’ятовують, що П неповне ділене 14 десятків, а Ш неповне ділене – 140 одиниць. 17640! 35... 175 504 140 В порядку ознайомлення показуємо учням письмове ділення багатоцифрового числа на трицифрове:
2527: 324 Перевіряємо: 8 * 300 = 2400, 2527 – 2400 = 127, 127 < 8 * 24, тому цифра 8 – не підходить; візьмемо по 7: 7 * 300 = 2100, 2527 – 2100 = 427, 427 > 7 * 24, цифру 7 пишу на місці десятків у частці. 2268 десятків розділилося. 259 десятків не розділилися. Остача 259 менша за дільник 324, цифру частки знайдено вірно. З остачі 259 десятків і 2 одиниць діленого утворюю друге неповне ділене – 2592 одиниці. 2592: 324 2592 одиниці розділилися. Усі одиниці розділилися, ділення закінчено.
Методика вивчення дробів
В результаті вивчення теми діти повинні засвоїти: 1) як утворюються дроби з знаменником 3,9,6,5,10,4,8; 2) навчитися записувати і читати дробові числа; 3) знати терміни “Чисельник” і “знаменник”, пояснювати значення кожної цифри в запису дробового числа; 4) вміти порівнювати дроби; 5) навчитися розв’язувати задачі на знаходження дробу від числа.
1. Ознайомлення з поняттям “дріб”. Утворення дробів показують на наочності. Ознайомленню з новим поняттям передує підготовча робота, під час якою актуалізується: - утворення частин, демонстрація,,,, і так далі; - значення числа під рискою (знаменника) і над рискою (чисельника.) - кількість рівних частин в цілому. Ознайомлення. Утворення дробу можна здійснити під час практичної роботи: Завдання 1.Візьміть риску паперу, розмалюйте.
- Скільки четвертих частин в цілому? (Чотири) - Якщо в цілому чотири чверті, то розмалюйте ще.
- Скільки всього четвертих частин ми розмалювали? (Дві четверті) + = * 2 = - по взяти 2 рази; читаємо так: “дві четвертих” - Розмалюйте три четвертих частини. + + = * 3 = - по взяти 3 рази; читаємо “три четвертих” - Такі числа є дробами. Дріб – це одна або кілька рівних частин цілого. Дроби записують двома натуральними числами, які розділені рискою. Число над рискою називають чисельником, а число під рискою називають знаменником. Знаменник показує на скільки рівних частин розділили ціле, а чисельник – скільки таких частин взяли.
Зауваження. При читанні дробів треба пам’ятати: чисельник дробу – кількісний числівник жіночого роду (одна, дві, три й тощо), а знаменник – порядковий числівник (дев’ята, сота, двісті тридцята): - п’ять шостих; - сім одинадцятих; - сімнадцять тридцять п’ятих. Завдання 2. На скільки рівних частин розділене ціле в кожному випадку? Що показує заштрихована частина кожного цілого? Яким дробом можна позначити заштриховану частину?
Завдання 3. Вкажи ціле, на якому заштриховано:
Завдання 4. Вибери із записаних дробів той, який показує, яку частину цілого заштрихували. Обведи та прочитай цей дріб:
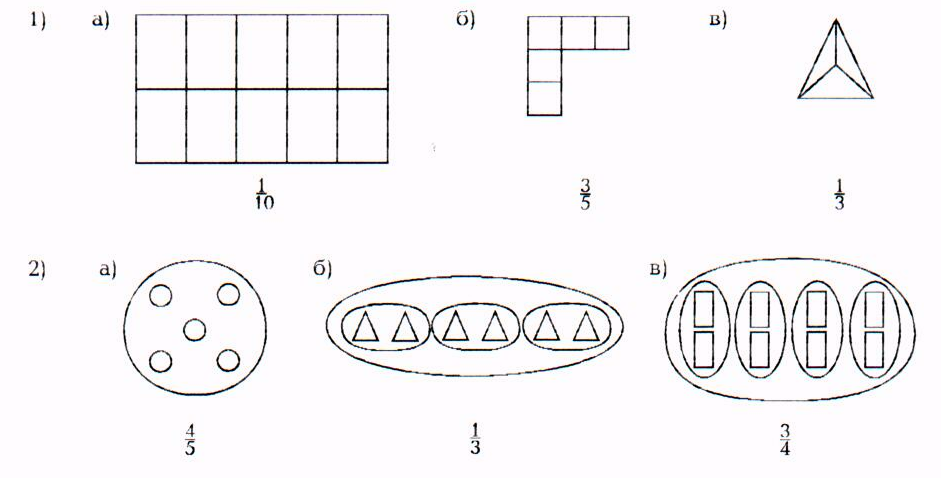
Завдання 6. Розмалювати частину цілого, яка відповідає дробу:
Треба зазначити, що на малюнку в) трикутник розбитий не на рівні частини, тому позначити Завдання 7. Розмалювати, якщо це можливо, частину цілого, яка відповідає дробу:
Зазначимо, що розмалювати зазначені частини фігур можливо лише на кресленнях № 1 б) і в) – лише на них фігури розбиті на рівні частини. Завдання 8. Розмалюй частину фігури так, щоб отримати візерунок. Запиши дріб, який показує, яку частину фігури ти розмалював. Чи можна цю частину розмалювати по-іншому? Як?
Завдання 9. Розмалюй частину цілого, яка відповідає дробу (покажи різні способи):
Завдання 10. Прочитай дроби. Назви чисельник і знаменник кожного дробу і поясни, що вони означають:;;;;. Завдання 11. Запиши цифрами дроби: - п’ять восьмих; - шість дев’ятих, - тринадцять двадцять восьмих; - тридцять три сотих. Завдання 12 Яку частину метру складає 1 дм? Подай в метрах 1 дм, 6 дм, 8 дм. Яку частину години складає 1 хвилина? Подай в годинах 1 хв., 5 хв., 17 хв., 27 хв. Яку частину року складає 1 місяць? 3 місці? 7 місяців? 9 місяців? 12 місяців? Запиши дроби. Завдання 13. Ціле поділили на 100 рівних частин. Як називаються 7, 9, 14, 16, 23, 42, 88 таких частин? Запиши відповідні дроби. Завдання 14. Розділи 9 яблук порівну між дванадцятьма дітьми. Скільки отримала кожна дитина? Постарайся знайти різні способи. - Подумай, чи можна розв’язати задачу, якщо жодне яблуко не можна ділити більш ніж на 4 рівні частини. - Постарайся знайти такий розв’язок (6 яблук треба розділити навпіл і дати кожній дитині половину яблука; а решту 3 яблука розділити на 4 рівні частини і дати кожній з дитин по чверті яблука, отже кожна з дванадцяти дитин отримує по половині і ще чверті яблука.) - Якщо тобі важко знайти такий розв’язок, зобрази кожне яблуко кругом і діли круги на рівні частини. Завдання 15. До чаю мама подала торт, який був розрізаний на 10 рівних шматочків.Брат з’їв 2 шматочка, а сестра – 1 шматок. Яку частину торту з’їв брат і яку сестра? Запиши числа. Поясни, що показує в них чисельник і що знаменник. Завдання 16. До чаю мама подала торт, який був розрізаний на 7 рівних шматочків. За столом сиділо 7 чоловік. Кожна людина з’їла по одному шматку. Яку частину торту з’їли? Запиши відповідь дробовим числом. - Чи залишилося щось від торту? Отже з’їли цілий торт! Чи можна замість дробу записати відповідь натуральним числом? - Чи вірно записати так: - Чим цікавий цей дріб? (В ньому чисельник дорівнює знаменнику і цей дріб дорівнює 1.) - Запиши інші дроби, які дорівнюють числу 1. Завдання17. - Коли дробове число дорівнює 1? Наведи приклади таких дробів. - Запиши в загальному вигляді ознаку, за якою можна впізнати, що дріб дорівнює 1. Якщо а=в, то - Якби в попередній задачі з’їли не 7 шматочків торту а менше семи, то щось лишилося б від цілого торту; не з’їли цілий торт! При якій умові дріб менший за 1? - Наведи при клади таких дробів. - Запиши в загальному вигляді ознаку цих дробів. Якщо а<в, то - За яких умов дріб буде більша за 1? Якщо а>в, то Завдання 18. Доведи, що дріб - Подумай, як можна отримати такий дріб? (Такий дріб можна отримати, якщо не одне ціле, а наприклад два цілих предмети поділити на 6 рівних частин кожний і взяти лише 8 таких частин.) - Склади задачу, яка б показала спосіб отримання такого дробу. - Сашко склав таку задачу: „ У дівчинки було дві плитки шоколаду „Мілка”. Кожна плитка шоколаду „Мілка” розділена на 24 маленькі прямокутники. Дівчинка з’їла 27 маленьких прямокутників шоколаду. Яку частину плитки шоколаду з’їла дівчинка?” Завдання 19. - Коли дробове число дорівнює 1?Наведи приклади таких дробів. - Запиши в загальному вигляді ознаку, за якою можна впізнати, що дріб дорівнює 1. Якщо а=в, то - А при якій умові дріб менший за 1?Чому ти так вважаєш? Наведи при клади таких дробів. - Запиши в загальному вигляді ознаку цих дробів. Якщо а<в, то - Наведи приклади дробів, які більші за число 1. - Запиши в загальному вигляді ознаку цих дробів. Якщо а > в, то
2. Порівняння дробів.
Проводиться на практичній основі, використовуючи риски паперу, круги, прямокутники. Спочатку порівнюємо дроби, засобом накладання відповідних частин рисок паперу. Завдання 1. Візьміть дві однакові риски паперу. Покажіть на першій дріб У наступному завданні можна зобразити дроби, як частини цілого відрізку, розмальовуємо їх різними кольорами і робимо висновок. Завдання 2. Накресліть відрізок довжиною 6 см. Позначте спочатку дріб та. Порівняйте ці дроби.
< Після розв’язання цього завдання можна обговорити питання: - Що спільного в цих дробах? (В них однакові знаменник.) Що вони означають? - Чим відрізняються ці дроби? (Чисельниками). Що означає чисельник першого дробу? Що означає чисельник другого дробу? - Чому <? (кожний відрізок поділили на 6 рівних частин, спочатку взяли 2 такі частини, а потім 4 такі частини; 2 частини менше, ніж 4 частини, тому <.) Отже, дроби з однаковими знаменниками можна порівнювати без наочності, засобом міркування: кожну величину поділили на однакову кількість частин, спочатку взяли..., потім взяли...:... такі частини Завдання 3. - Розглянь малюнок:
Скільки на ньому рівних квадратів? - Яку частину великого квадрату складає один маленький? Запиши відповідь дробом. - Які ще дроби можна записати, використовуючи цей малюнок? Запиши ці дроби. - Для кожного записаного дробу зроби такий самий малюнок і зафарбуй на ньому ту частину великого квадрата, яка дорівнює цьому дробу. - На якому малюнку площа зафарбованої частини найменша? Найбільша? - Розташуй записані тобою дроби в порядку зростання площин, що їм відповідають. - Порівняй дроби. Що в них не змінюється? Що змінюється? - Як змінюються чисельники? Як змінюються дроби? - Який висновок можна зробити?
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1955; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.011 с.) |

 7 7: 3
7 7: 3  9, 9: 3
9, 9: 3  31: 7, буде приблизно по 4. 4 – це пробна цифра, її слід перевірити: 4 множимо на десятки дільника, буде 280; віднімаю отримане число з неповного діленого (315 – 280), буде 35; порівнюю остачу з добутком пробної цифри на дільник (4 * 1); остача більша, тому пробна цифра підходить, пишу її на місці сотень в частці.
31: 7, буде приблизно по 4. 4 – це пробна цифра, її слід перевірити: 4 множимо на десятки дільника, буде 280; віднімаю отримане число з неповного діленого (315 – 280), буде 35; порівнюю остачу з добутком пробної цифри на дільник (4 * 1); остача більша, тому пробна цифра підходить, пишу її на місці сотень в частці. від 80 т
від 80 т




 Завдання 5. Запиши дроби, які показують, яку частину цілого заштрихували:
Завдання 5. Запиши дроби, які показують, яку частину цілого заштрихували:
 не можливо. Дітям можна пояснити, що це „ловушка”, такі „ловушки” зустрічаються у завданнях, щоб вони були уважніші!
не можливо. Дітям можна пояснити, що це „ловушка”, такі „ловушки” зустрічаються у завданнях, щоб вони були уважніші!


 = 1?
= 1? = 1.
= 1. більша, ніж число 1.
більша, ніж число 1. , а на іншій Способом накладання відповідних частин порівняйте дроби
, а на іншій Способом накладання відповідних частин порівняйте дроби 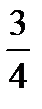 та.
та.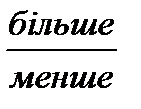 , ніж... такі частини, тому дріб...
, ніж... такі частини, тому дріб... 



