Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометричні фігури та величини.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В четвертому класі узагальнюється та систематизується геометричний матеріал, який вивчався в 1-3 класах. Доповнюються та узагальнюються властивості геометричних фігур, а також вивчаються нові геометричні фігури. Первинними поняттями в геометрії є – точка, пряма, площина. Вони вводяться без визначення (про них кажуть, що це невизначувані поняття), лише спираючись на досвід дитини. Всі інші поняття визначаються через первинні або ті, що були визначені раніше. Наприклад: Відрізок – це частина прямої, яка складається з усіх точок прямої, що лежать між двома даними точками на прямій. Ці точки називають кінцями відрізка. А В Інакше: відрізок – це частина прямої, Яка обмежена двома точками. Позначаємо: АВ. Промінь – це частина прямої, яка складається з усіх точок цієї прямої, що лежать по один бік від даної на прямій точки. Ця точка – початок променя. А Точка А розбила пряму на два променя в а а і в, які мають спільний початок. О М В О
Кут – це фігура, яка складається з точки – вершини – вершини кута - та двох різних променів, що виходять з цієї точки – сторін кута. А Кут можна позначати: однією буквою - В трьома буквами, серед яких позначення вершини ставиться в середині - С За величиною кути поділяються на прямі, гострі і тупі. Як відомо, поняття про прямий кут учні отримують з практичного досвіду (при подвійному перегинанні аркуша паперу). Гострий кут менше прямого, тупий кут більше, ніж прямий. D В С На цьому малюнку:
О А Одна з найбільш відомих учням фігур – трикутник. Трикутник – це геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій і трьох відрізків, які послідовно з’єднують ці точки. В Точки А, В, С – вершини трикутника, відрізки АВ, ВС та АС сторони трикутника. С Кожні дві сторони трикутника утворюють А кут. Отже, елементи трикутника: Вершини (точки А,В,С) Сторони (відрізки АВ, ВС, АС, іноді довжини сторін позначають а, в, с) Кути ( За величиною кутів поняття „трикутник” можна класифікувати:
В гострокутному трикутнику всі кути гострі. В прямокутному трикутнику один з кутів прямий, два інші гострі. В тупокутному трикутнику один з кутів тупий, два інших гострі. Учні повинні знати: в трикутнику не може бути більш, ніж один прямий кут, або більш, ніж один тупий кут.
Завдання. Позначте на малюнку вершини гострокутного трикутника А,В,С; вершини прямокутного В,С, D; вершини тупокутного А,В, D. За довжиною сторін поняття „трикутник” класифікується так:
Трикутник – це многокутник з найменшою кількістю сторін (кількість сторін 3, вершин 3, кутів 3). Учні знайомі також з чотирикутниками, п’ятикутниками, шестикутниками (відповідно кількість сторін – 4, 5, 6). А В С D А D
М Е С D В Е Серед чотирикутників виділяються окремі види: прямокутники і квадрати (іноді учнів знайомлять ще й з ромбами). Прямокутнику та квадрату дається визначення через найближчий рід та видові ознаки:
Прямокутник – це чотирикутник, у якого всі кути прямі. (найближчий рід) (видові ознаки) Квадрат – це прямокутник, у якого всі сторони рівні. (найближчий рід) (видові ознаки) Квадрат можна було б визначити і так: квадрат – це чотирикутник, у якого кути прямі і сторони рівні. Але чотирикутник не є найближчим родом для поняття „квадрат”, тому прийшлось збільшити кількість видових ознак. В С АВСD – прямокутник. Властивості прямокутника: АВ = СD, ВС = АD (протилежні сторони рівні) А D Властивості прямокутника не згадують при його означення. С D Е В D С М Е В А А На малюнку зображені многокутники: п’ятикутник та шестикутник. Вершина А п’ятикутника з’єднана відрізками з двома не сусідніми його вершинами С і D. АС і АD – діагоналі п’ятикутника. Взагалі – відрізок, який з’єднує дві не сусідні вершини многокутника називається діагоналлю. Скільки діагоналей можна провести в п’ятикутнику? Проведемо міркування: кожну вершину п’ятикутника можна з’єднати діагоналлю лише з двома вершинами (крім самої вершини та двох сусідніх вершин). Чи вірно, що всього діагоналей у п’ятикутника 2 * 5 = 10? Ні, бо таким способом кожна діагональ враховується двічі (діагональ АС та СА, але ж цей відрізок той самий). Тому кількість діагоналей п’ятикутника 10: 2 = 5. Такі ж самі міркування дають змогу сказати, що у шестикутника всього ((6 – 3) * 6): 2 діагоналей, тобто 9 діагоналей. У чотирикутнику всього дві діагоналі. В прямокутнику та в квадраті діагоналі рівні. В трикутнику зовсім не можна провести діагоналей, бо для кожної його вершини інші вершини – сусідні. В початковій школі, крім фігур обмежених ламаною вивчаються фігури, які обмежені кривою лінією. Найпростішою з таких фігур є коло. Візьмемо довільну точку О на площині та відкладемо від неї відрізки D однакової довжини. Одержимо множину точок, які А знаходяться на рівних відстанях від вибраної точки О. Ця множина точок і складає фігуру, що називається О колом. В С Елементи кола: центр О, відрізок ОА – радіус кола, відрізок ВС, що з’єднує дві будь-які точки кола, хорда; М хорда DМ, яка проходить через центр, діаметр кола. Коло обмежує частину площини, яка разом з колом становить геометричну фігуру – круг. А Яку б точку цієї фігури ми не взяли, вона знаходиться від центра кола на відстані, яка дорівнює радіусу (ОА) або О менше радіуса (ОА). Точка В – внутрішня точка круга, А В лежить на границі круга, якою є коло.
Виділимо такі частини круга: сегмент та сектор. Сегмент – це частина круга, D яка обмежена хордою СD та С дугою кола. С1 О Хорда розбиває круг на два В сегменти. С2 А Сектор – це частина, яка обмежена двома радіусами ОА та ОВ і дугою кола. А
О В сегментом, так і сектором.
Геометричні тіла
циліндр куб куля конус паралелепіпед трикутна піраміда
Циліндр, куб, куля, конус, паралелепіпед, піраміда - це геометричні тіла, тобто просторові фігури.
круг квадрат прямокутник трикутник п’ятикутник
Круг, квадрат, прямокутник, трикутник, п’ятикутник – це плоскі фігури. Завдання. Знайдіть плоскі фігури у геометричних тілах. 1) В яких геометричних тілах є круг? (У циліндрі, шарі, конусі.) 2) В яких геометричних тілах є квадрат? (У кубі.) 3) В яких геометричних тілах є трикутник? (У піраміді.) Побудова геометричних фігур Необхідно навчити учнів виконувати побудови: кола, трикутника, прямокутника. Усі побудови будемо виконувати за допомогою таких приладів – лінійка та циркуль. Задача 1. Побудувати коло з радіусом, який дорівнює 3 см. А Побудова 1) Візьми довільну точку у зошиті і познач її літерою О – це буде центр кола. О 2) Розчином циркуля на лінійці відмір відрізок 3 см. 3) Гостру ніжку циркуля постав у точку О, а іншою ніжкою циркуля проведи замкнену лінію – коло. В 4) Поєднай будь-яку точку кола з центром – точкою О. Ти отримав радіус, наприклад ОА. Виміряй довжину цього відрізку: ОА = 3 см. 5) Продовж за допомогою лінійки радіус у інший бік до перетину з колом. Отримали відрізок АВ – це діаметр кола. 6) Виміряй довжину відрізку АВ. АВ = 6 см. 7) Скільки радіусів містить АВ? АВ = 2 ОА. Зроби висновок.
Задача 2. За допомогою циркуля та лінійки побудуй трикутник, сторонами якого були б дані відрізки: а Побудова в 1) Проведи за допомогою лінійки довільну с пряму і відміть на ній точку А. 2) Розчином циркуля відмір відрізок а та відклади його на прямій від точки А, К отримаємо точку В, отже АВ = а. 3) З точки А, як із центру розчином циркуля, що дорівнює відрізку „ в ” проведи коло. 4) З точки В, як із центру, розчином циркуля, А В який дорівнює відрізку „ с ”, проведи коло. 5) Точку перетину кіл познач літерою К. З’єднай точку К з точками А та В. Ти отримав трикутник АКВ із заданими довжинами сторін! Задача 3. Побудувати прямокутник, довжини сторін якого 4 см та 3 см. 4 см Побудова 1) На прямій а вибери довільну точку А. 3 см 2) З вершиною в точці А за допомогою косинця побудуй прямий кут. 3) На одній із сторін прямого кута від вершини А відкладемо за допомогою С Д циркуля відрізок АВ, який дорівнює 4 см. 4) На іншій стороні прямого кута від вершини відкладемо за допомогою циркуля відрізок ВД, який дорівнює А В 3 см. 5) З вершиною у точці В за допомогою косинця, побудуємо прямий кут. 6) На стороні прямого кута з вершиною в точці В, від цієї точки відкладемо відрізок ВД, який дорівнює 3 см. 7) Поєднаємо точки С і Д. Чотирикутник АВДС – шуканий прямокутник. Задачі на обчислення периметра і площі Задача 1. За кресленням та записам склади і розв’яжи задачу: А АО = АЕ ОЕ = 18 см Р = 72 см О Е АО -? Р – позначення периметра. Периметр – це сума довжин усіх сторін многокутника. Р = АО + АЕ + ОЕ 72 = АО + АО + 18 72 = 2 АО + 18 2АО = 72 – 18 2АО = 54 АО = 54: 2 АО = 27 (см) Відповідь: АО = 27 см. Задача 2. В трикутнику АВС, кут С – прямий, АС = 3 см, ВС = 4 см. Побудуй такий трикутник, виміряй сторону АВ і знайди периметр трикутника АВС. А Сторона АВ = 5 см. У математиці прямокутні Трикутник зі сторонами 3,4, 5 називається 3 см Єгипетським трикутником. Р = АС + ВС + АВ; Р = 3 + 4 + 5 = 12 (см) В 4 см С Відповідь: периметр трикутника 12 см. Задача 3. Накресли такий квадрат у зошиті і обчисли його периметр. а = 35 мм Р = а * 4 Р -? Р = 35 * 4 = 140 (мм) Відповідь: 144 мм периметр квадрата.
Задача 4. Накресли довільний прямокутник, периметр якого 12 см. Позначимо довжину прямокутника а, а ширину в, тоді в периметр дорівнює Р = (а + в) * 2. Знайдемо суму двох суміжних сторін: а + в = Р: 2; отже сума двох суміжних сторін дорівнює половині периметра а + в = 12: 2; а а + в = 6 (см). Які можливі варіанти? 1) а = 1, в = 5; Р = (1 + 5) * 2 = 12 (см) 1 см 5 см 2) а = 2, в = 4; Р = (2 + 4) * 2 = 12 (см)
2 см
4 см 3) а = 3, в = 3; Р = а * 4; Р = 3 * 4 = 12 (см)
3 см
3 см Задача 5. Накресли за допомогою циркуля коло, радіус якого 35 мм. Поділи його на 6 рівних частин. (Не змінюючи розчину циркуля діли цим розчином коло: постав гостру ніжку циркуля у будь-яку точку кола, а іншою ніжкою відміть наступну точку; постав гостру ніжку циркуля у отриману точку і відміть наступну точку, і так далі... Таким чином, коло поділиться на 6 рівних частин. Точки ділення кола пронумеруй поступово: 1, 2, 3, 4, 5, 6.) Поєднай точки 1, 3, 6 відрізками. Познач отриманий трикутник літерами КМN. Виміряй лінійкою сторони і обчисли периметр цього трикутника. 6 О N = ОК = r = 35 мм; М N = 35 мм N М NК = 70 мм; МК = 61 мм 5 1 Р = NК + NМ + МК; Р = 70 + 35 + 61 = 166 (мм) О Відповідь: периметр трикутника NМК дорівнює 166 мм. 4 2
К 3
Задача 6. Довжина відрізку АВ = 6 см. Радіус кола з центром в точці А дорівнює 2 см 4 мм, а з центром в точці В - дорівнює 1 см 8 мм. Знайди відстань КМ та СД.
К А С Д В М
1) АВ = АС + СД + ДВ. Замінимо складені іменовані числа простими: 2 см 4 мм = 24 мм, 1 см 8 мм = 18 мм, 6 см = 60 мм. Маємо: 60 = 24 + СД + 18; 60 = СД + 42; СД = 60 – 42; СД = 18 мм = 1 см 8 мм. 2) КМ = КС + СД + ДМ КМ = 24 * 2 + 18 + 18 * 2 = 48 + 18 + 36 = 102 (мм) = 10 см 2 мм Відповідь: 10 см 2 мм, 1 см 8 мм. Задача 7. Знайди площу фігури за планом: В 50 м С S3 40 м S1 S2 30 м А 70 м Д 1 спосіб. Розіб’ємо фігуру на два прямокутника. Sфігури = S1 + S2 , S1 = 50 * 40 = 2000 (м2) = 20 ар S2 = (70 – 50) * 30 = 20 * 30 = 600 (м2) = 6 ар Sфігури = 20 + 6 = 26 (ар) П спосіб. Доповнимо фігуру до більшого прямокутника. Sфігури = SАВСД – S3. Площа великого прямокутника: SАВСД = 70 * 40 = 2800 (м2) = 28 ар S3 = (70 – 50) * (40 – 30) = 20 * 10 = 200 (м2) = 2 ар Sфігури = 28 – 2 = 26 (ар) Відповідь: площа фігури 26 ар. Задача 8. Периметр прямокутної ділянки 296 м. Довжина ділянки 96 м. Знайди площу ділянки. 1) Р = (а + в) * 2 а + в = 296: 2; а + в = 148 (м) 2) Довжина прямокутної ділянки відома із умови, підставимо значення довжини: 96 + в = 148 3) S = а * в; S = 96 * 52 = 4992 (м2) = 49 а 92 м2 Задача 9. Довжина прямокутної ділянки 120 м, ширина 46 м. Знайти ширину іншої прямокутної ділянки, з такою самою площею, довжина якого 80 м. 1) Знайдемо площу першої ділянки: S = а * в; S = 120 * 46 = 5520 (м2) 2) Площа іншої ділянки така сама: S = 55 20 м2; S = а * в; 5520 = 80 * в Відповідь: ширина іншої ділянки 69 м. Задача 10. Периметр трикутника 186 мм. Довжина однієї сторони 42 мм, інша сторона в 2 рази більша за першу. Чому дорівнює довжина третьої сторони.
1) 42 * 2 = 84 (мм) – довжина другої сторони 2) 42 + 84 = 126 (мм) – сума довжин першої та другої сторін 3) 186 – 126 = 60 (мм) – довжина третьої сторони. Відповідь: 60 мм. Задача 11. Побудуй три прямокутника так, щоб площа кожного дорівнювала 16 см2, а периметр першого – 16 см, другого – 20 см, третього – 34 см. Площа прямокутника: S = а * в; S = 16 см 2 Периметр прямокутника: Р (а + в) * 2 1) Периметр першого прямокутника – 16 см. а + в = 16: 2; а + в = 8 см Отже маємо: S = 16 см2, а + в = 8 см Які можливі варіанти? а = 1, в = 7 S1 = 7 – не підходить а = 2, в = 6 S1 = 12 – не підходить а = 3, в = 5 S1 = 15 – не підходить а = 4, в = 4 S1 = 16 – підходить У першого прямокутника сторони а = 4 см, в = 4 см, тому це квадрат. 2) Периметр другого прямокутника 20 см. а + в = 20: 2; а + в + 10 (см) і S = 16 см2 а = 1, в = 9 S1 = 9 – не підходить а = 2, в = 8 S1 = 16 – підходить У другого прямокутника сторони рівні а = 2 см, в = 8 см або навпаки – а = 8 см та в = 2 см. 3) Периметр третього прямокутника 34 см. Маємо а + в = 34: 2; а + в = 17 (см) і S = 16 см2 а = 1, в = 16 S1 = 16 – підходить У третього прямокутника сторони рівні а = 1 см, в = 16 см або навпаки а = 16 см, в = 1 см. Задача 12. Ширина прямокутника 8 см, а довжина у 4 рази більша. Чому дорівнює площа прямокутника? S = а * в; S = 8 * (8 * 4) = 8 * 32 = 256 (см 2) Відповідь: 256 см2 Задача 13. Сторона рівностороннього трикутника 8 см. Знайди площу квадрата, пери метр якого дорівнює периметру цього трикутника. Периметр рівностороннього трикутника: Р = а * 3; Р = 8 * 3 = 24 (см). Периметр квадрата дорівнює периметру трикутника: Р = 24 см. Р = а * 4; 24 = а * 4 S = а * а; S = 6 * 6 = 36 (см2) Відповідь: площа квадрата 36 см2. Задача 14. Площа прямокутника 30 см2, одна з його сторін 5 см. Знайди довжину іншої сторони прямокутника. S = а * в; 30 = 5 * в Відповідь: інша сторона прямокутника 6 см. Задача 15. Знайди розміри невідомих сторін прямокутника за малюнком:
2 см 12 см2? 8 см2
? 4 см 1) Площа першого прямокутника: S = а * в; 12 = а * 2 а = 6 см. 2) Площа другого прямокутника: S = а * в; 8 = 4 * в в = 2 см. Відповідь: 6 см та 2 см. Задача 16. Периметр прямокутника 24 дм. Ширина на 4 дм менше довжини. Знайти площу прямокутника. Р = (а + в) * 2 а дм – довжина прямокутника, тоді за умовою задачі (а – 4) дм – ширина прямокутника. Підставимо їх у останню формулу: а + а – 4 = 12; 2 * а – 4 = 12 S = а * в; S = 8 * 4 = 32 (см2) Відповідь: 32 см2. Задача 17. Периметр прямокутника 54 м. Його довжина в 2 рази більше ширини. Чому дорівнює площа прямокутника? 1) Р = (а + в) * 2 в – ширина, а довжина – в * 2. Підставимо ці значення: в * 2 + в = 27; 3 * в = 27 2) S = а * в; S = 18 * 9 = 162 (м2) = 1 а 62 м2. Відповідь: 1 а 62 м2. Задача 18. Є три прямокутника: перший зі сторонами 5 см та 3 см, другий зі сторонами 5 см та 4 см, третій зі сторонами 7 см та 2 см. Чи можна з них скласти квадрат? 1) Знайдемо площі цих прямокутників: S1 = 5 * 3 = 15 (см2); S2 = 5 * 4 = 20 (см2); S3 = 7 * 2 = 14 (см2) 2) Знайдемо суму площ трьох прямокутників: S = 15 = 20 + 14 = 49 (см2) Отже, площа фігури, яку складено з трьох прямокутників дорівнює 49 см2. Це може бути квадрат зі стороною 7 см 5 см
4 см П 7 см Ш 3 см 1
5 см 2 см Завдання 19. Площа прямокутника 120 см2, а ширина 10 см. Ширину цього прямокутника зменшили у 2 рази, а довжину збільшили в 6 разів. У скільки разів збільшилася площа? 1) S = а * в; 120 = а * 10 S – добуток, а – перший множник, в – другий множник 2) Ширину зменшили у 2 рази, а якщо один з множників зменшити у 2 раз, то й добуток - площа – зменшиться в 2 рази. Маємо 120: 2 = 60 (см2) 3) Довжину збільшили у 6 разів. Якщо другий множник збільшити у 6 разів, то й добуток – площа – збільшиться у стільки ж разів. Маємо: 60 * 6 = 360 (см 2) 4) У скільки разів збільшилася площа? 360: 120 = 3 – у 3 рази. Можна міркувати інакше: Якщо один множник зменшити у 2 рази, а другий множник збільшити у 6 разів, то добуток збільшиться у 3 рази (6: 2 = 3). Тому площа збільшиться у 3 рази. Відповідь: у 3 рази. Завдання 20. Чи вірне твердження: „чотирикутник, у якого усі сторони рівні 10 см, є квадратом”? Не вірно, тому що квадрат – це прямокутник, у якого всі сторони ріні; а в умові сказано про чотирикутник, у якого всі сторони рівні. Або: квадрат – це чотирикутник, у якого: 1) усі кути прямі; 2) усі сторони рівні. В умові задачі не говориться, що у даного чотирикутника усі кути прямі. Завдання 21. Площі двох прямокутників 20 см2 та 25 см2. Який з них може бути квадратом? Sкварата = а * а, тому числове значення площі повинно бути таким, щоб його можна було подати у вигляді добутку двох однакових множників. Лише число 25 можна подати у вигляді такого добутку: 25 = 5 * 5, тому прямокутник із площею 25 см2 може бути квадратом. Завдання 22. Чи можна прямокутник з сторонами 8 см та 16 см розбити на два квадрати?” Квадрат – це прямокутник. Тому, можливо було б розбити прямокутник на два квадрати. Але у квадрата всі сторони повинні бути рівними. В даному прямокутнику довжина в два рази більше за ширину, тому якщо довжину розбити на два рівних відрізка, то й отримаємо два квадрати (з стороною 8 см), на які розбитий даний прямокутник. Даний прямокутник можна розбити на:
А можна розбити: 5 квадратів 8 квадратів
Обчислення повної поверхні куба та паралелепіпеда
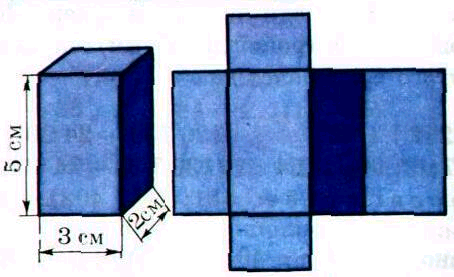
Задача 1. Довжина ребра куба дорівнює 2 см. Скільки квадратних сантиметрів паперу треба, щоб обклеїти усі грані куба? У куба 8 вершин, 12 ребер, 6 граней. Кожна грань – квадрат. S = Sкв. * 6; площа квадрата зі стороною 2 см дорівнює: Sквадрата = а * а = 2 * 2 = 4 (см2) Отже, S = 4 * 6 = 24 (см2) Відповідь: 24 см2 паперу треба, щоб обклеїти усі грані куба з довжиною ребра 2 см. Задача 2. За даними малюнка обчисли площу поверхні розгортки прямокутного паралелепіпеда:
У паралелепіпеда протилежні грані рівні, тому достатньо обчислити площі трьох граней і отриману суму подвоїти: S = (а * в + а * с + в * с) * 2. Маємо: S = (3 * 2 + 3 * 5 + 2 * 5) * 2 = 31 * 2 = 62 (см2) Відповідь: 62 см2. Задача 3. Ящик має форму прямокутного паралелепіпеда. Його розміри: довжина 4 дм, ширина 3 дм, висота 2 дм. Скільки квадратних дециметрів паперу треба, щоб обклеїти усі грані ящика? S = (а * в + а * с + в * с) * 2; S = (4 * 3 + 4 * 2 + 3 * 2) * 2 = 52 (см2) Відповідь: 52 см2. Задача 4. Дано прямокутний паралелепіпед, його довжина 40 м, ширина 30 м, висота 50 м. Знайдіть площу повної поверхні паралелепіпеда. S = (а * в + а * с + в * с) * 2; S = (40 * 50 + 40 * 30 + 50 * 30) * 2= 9400 (м2) = 94 ар Відповідь: 94 ари.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.184 (0.01 с.) |

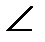 В, яка означає вершину кута;
В, яка означає вершину кута; с)
с)
 півкруга (цю фігуру можна назвати як
півкруга (цю фігуру можна назвати як а + в = Р: 2.
а + в = Р: 2.