
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Узагальнення обчислювальних прийомів поза табличного множення і діленняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Знаходження результатів добутку та частки у певних випадках обчислення можна знаходити різними способами: Множення і ділення розрядного числа на одноцифрове
Ділення розрядного числа на розрядне
Множення і ділення двоцифрового і трицифрового числа на одноцифрове
Ділення двоцифрового числа на двоцифрове
Таким чином, усі випадки поза табличного множення і ділення можна обчислити застосовуючи прийоми: 1. Укрупнення розрядних одиниць. 2. На підставі множення (ділення) добутку на число. 3. На підставі ділення числа на добуток. 4. На підставі конкретного змісту дії ділення. 5. На підставі множення (ділення) суми на число. Оскільки ці прийоми застосовуються для різних випадків обчислення, то при повторенні матеріалу слід узагальнити зміст обчислювального прийому для різних випадків обчислення. Результати узагальнення наведемо в формі пам’яток.
Прийом на підставі конкретного змісту дії ділення 1. Розділити число а на число в, означає знайти таке число с, яке при множенні на дільник в, дає ділене а. а: в = с, тому що с * в = а 2. Підбираю таке число.
|
| Пам’ятка Прийом на підставі ділення числа на добуток 1. Замінюю дільник добутком двох чисел. 2. Застосовую правило ділення числа на добуток: спочатку ділю на один множник, а потім результат ділю на інший множник. 40: 20 = 40: (2 * 10)=(40:10): 2 =2 360: 30 = 360: (3*10) = (360:10):3 = 12 72: 36 = 72: (9 * 4) = (72: 9): 4 = 2 144: 24 = 144: (6 * 4) = (144: 6): 4 = 6 |
Пам’ятка
Прийом на підставі множення (ділення) суми на число
1. Подаю двоцифрове число у вигляді суми двох доданків.
2.  кожний доданок на число.
3. Додаю отримані результати.
17 * 4 = (10 + 7)*4 = 10*4 + 7*4 =68 320 * 3 = (300+20)*3=300*3 + 20*3=960
45: 3 = (30 + 15): 3= 30:3 + 15: 3=15 240: 5 = (200+40):5= 200:5 + 40: 5 = 48 кожний доданок на число.
3. Додаю отримані результати.
17 * 4 = (10 + 7)*4 = 10*4 + 7*4 =68 320 * 3 = (300+20)*3=300*3 + 20*3=960
45: 3 = (30 + 15): 3= 30:3 + 15: 3=15 240: 5 = (200+40):5= 200:5 + 40: 5 = 48
|
До випадків поза табличного ділення відноситься ділення з остачею. Наведемо алгоритм виконання ділення з остачею.
Ділення з остачею
| Пам’ятка 1. Називаю усі числа, які менші за ділене й діляться на дільник. 2. Найбільше з них ділю на дільник і результат записую в частці. 3. Віднімаю знайдене число від діленого, отримую остачу. 4. Записую розв’язання. Наприклад: 16: 3 1) 3,6,9,12, 15. 2) 15: 3 = 5 – частка 3) 16 – 15 = 1 – остача 4) 16: 3 = 5 (ост 1.) |
В 4-му класі учнів можна познайомити з раціональними способами обчислення добутку та частки. Розглянемо ці прийоми.
Правило множення на 9, 99, 999
Прийом подання одного з множників у вигляді різниці двох чисел.
| а * 9 = а * 10 - а а * 99 = а * 100 - а а * 999 = а * 1000 - а |
23 * 9 = 23 * 10 – 23 = 230 – 23 = 207
7 * 99 = 7 * 100 – 7 = 700 – 7 = 693
Правило множення у випадках, якщо один з множників близький до розрядного двоцифрового або трицифрового числа
Прийом подання одного з множників у вигляді різниці двох чисел.
Наприклад:
68 * 5 = (70 – 2) * 5 = 70 * 5 – 2 * 5 = 350 – 10 = 340
599 * 8 = (600 – 1) * 8 = 600 * 8 – 8 = 4800 – 8 = 4792
Правило множення на 11, 101, 1001
Прийом подання одного з множників добутку у вигляді суми двох чисел.
| а * 11 = а * 10 + а а * 101 = а * 100 + а а * 1001 = а * 1000 + а |
47 * 11 = 47 * 10 + 47 =470 + 47 = 517 23 * 101 = 23 * 100 + 23 = 2323
Існує інше правили множення на 11: щоб помножити двоцифрове число на 11, достатньо роздвинути його цифри і вставити між ними їх суму; при чому, якщо ця сума є двоцифровим числом, то її одиниці вставляються між цифрами даного числа, а десятки додаються до першої цифри.
Наприклад: 53 * 11
знаходимо суму 5 + 3 = 8;
роздвигаємо цифри числа 53, вставляємо між ними цифру 8, отримуємо відповідь: 53 * 11 = 583.
58 * 11
знаходимо суму 5 + 8 = 13;
роздвигаємо цифри числа 58, вставив між ними цифру 3, десятки збільшуємо на 1 (5 + 1 = 6), отримуємо відповідь: 58 * 11 = 638
Для того, щоб двоцифрове число помножити на 101, достатньо два рази записати дане число.
|
| Поделиться: |

 . Пам’ятаю, що при діленні іменованого числа на відлучене число отримаємо іменоване число; при ділені іменованого числа на іменоване – отримаємо відлучене число.
3. Записую (читаю) відповідь.
40 * 2 = 4д. * 2 = 8д. = 80 320 * 3 = 32д. * 3 = 96д. = 960
40: 2 = 4д.: 2 = 2д. = 20 360: 3 = 36д.: 3 =12д. = 120
40: 20 = 4д.: 2д. = 2 360: 30 = 36д.: 3д. =12
. Пам’ятаю, що при діленні іменованого числа на відлучене число отримаємо іменоване число; при ділені іменованого числа на іменоване – отримаємо відлучене число.
3. Записую (читаю) відповідь.
40 * 2 = 4д. * 2 = 8д. = 80 320 * 3 = 32д. * 3 = 96д. = 960
40: 2 = 4д.: 2 = 2д. = 20 360: 3 = 36д.: 3 =12д. = 120
40: 20 = 4д.: 2д. = 2 360: 30 = 36д.: 3д. =12
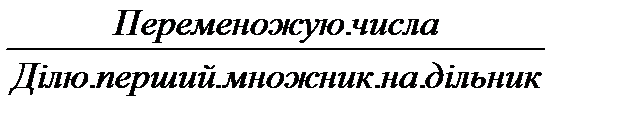 3. Результат множу на розрядну одиницю.
40 * 2 = (4 * 10)* 2 = (4 * 2) * 10 =80 320 * 3 = (32*10) * 3 = (31*3) *10=960
40: 2 = (4 * 10): 2 = (4: 2) *10 =20 360: 3 = (36 * 10): 3 =(36: 3)*10 =120
3. Результат множу на розрядну одиницю.
40 * 2 = (4 * 10)* 2 = (4 * 2) * 10 =80 320 * 3 = (32*10) * 3 = (31*3) *10=960
40: 2 = (4 * 10): 2 = (4: 2) *10 =20 360: 3 = (36 * 10): 3 =(36: 3)*10 =120



