
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зміст курсу математика 4-го класуСодержание книги
Поиск на нашем сайте
Програма з математики 4-го класу будується по основним лініям, визначеним Державним стандартом початкової загальної освіти: 1. Числа і дії над ними: - усна нумерація чисел багатоцифрових чисел; - письмова нумерація багатоцифрових чисел; - порівняння багатоцифрових чисел; - арифметичні дії додавання і віднімання, пов’язані з нумерацією чисел; - додавання і віднімання багатоцифрових чисел; - додавання і віднімання іменованих чисел; - залежність між компонентами та результатом арифметичних дій додавання і віднімання; - перевірка дій додавання і віднімання; - письмове множення і ділення багатоцифрових чисел на одно- та двоцифрові числа; - перевірка дій множення і ділення; - множення і ділення іменованих чисел; - закони арифметичних дій: додавання і множення; - дроби; знаходження дробу від числа; порівняння дробів з однаковими знаменниками. 2. Числові та буквені вирази: - числові вирази з дужками і без дужок; - знаходження значень буквених виразів, які містять одну – дві змінні; - запис буквами властивостей арифметичних дій; - розв’язування задач з буквеними даними. 3. Рівняння і нерівності: - рівняння з однією змінною типу: 17 – х = 50 – 30, (16 + х) – 34 = 10; - нерівності із змінною. 4. Геометричні фігури та їх властивості: - геометричні тіла: призма (паралелепіпед, куб), піраміда, конус, куля, циліндр (їх форма і назва); - побудова кола за допомогою циркуля; діаметр кола; 5. Величини і одиниці вимірювання величин: - довжина (таблиця співвідношення одиниць довжини); - маса (одиниці вимірювання: 1 т; співвідношення одиниць вимірювання маси); - час (співвідношення між одиницями часу) задачі на час; - поняття про площу; міри площі: квадратний сантиметр, квадратний дециметр, квадратний метр, 1 ар, 1 гектар, квадратний кілометр; правило знаходження площі прямокутника; знаходження довжини однієї з сторін прямокутника за його площею та відомою довжиною іншої сторони; визначення площі прямокутної ділянки за її планом; знаходження площі фігур за допомогою палетки; задачі, пов’язані з периметром та площею прямокутника. 6. Задачі: - задачі на знаходження четвертого пропорційного, що розв’язуються двома способами: способом наведення до одиниці та способом відношень. - задачі, пов’язані з одиничною нормою. - задачі на подвійне наведення до одиниці. - задачі на спільну роботу - задачі на знаходження невідомих компонентів за сумою трьох та сумою двох доданків. - задачі на пропорційне ділення. - задачі на знаходження невідомого за двома різницями. - задачі на знаходження середнього арифметичного. - складені задачі, які містять знаходження дробу від числа та числа за його дробом. В новій програмі не визначені питання: - знаходження числа за його дробом; - дріб, як частка двох натуральних чисел; - задачі на рух; - складені задачі, які містять дроби. Між тим, включено питання про зміну результатів арифметичних дій додавання і віднімання в залежності від зміни компонентів. За новою програмою учні 4-го класу на кінець навчального року повинні знати: - назви і послідовність натуральних чисел від 1 до 1000000, місце нуля у розширеному ряді, десятковий склад чисел; - напам’ять таблиці додавання і множення одноцифрових чисел та відповідні випадки віднімання і ділення; - порядок виконання дій у виразах; - назви і позначення одиниць величин – довжини (км, м, дм, см, мм), маси (кг, г, т, ц), площі (м2, дм2, см2, га, ар), швидкості (км/год, м/с), часу (год, хв,с), об’єму (л), вартості (грн..,к.); - співвідношення між одиницями довжини, площі, маси, часу, грошовими одиницями; - залежність між швидкістю, часом і відстанню; між ціною, кількістю і вартістю; між площею і довжинами сторін прямокутника; між компонентами і результатами дій; - залежність результату дії від зміни компонентів. Учні повинні вміти: - читати, записувати і порівнювати числа в межах мільйона; - називати компоненти арифметичних дій і читати найпростіші вирази (сума, різниця, добуток, частка); - виконувати усні і письмові обчислення в межах 100 на всі арифметичні дії; - виконувати письмові обчислення: додавання і віднімання в межах мільйона, множення і ділення на одно- та двоцифрові числа; - знаходити значення числового виразу на 3 – 4 арифметичні дії; - розв’язувати рівняння ускладненої структури з однією змінною; - виконувати підбір значень змінної у нерівностях; - розв’язувати прості текстові арифметичні задачі, пов’язані з відношенням більше (менше): задачі на збільшення (зменшення) числа на кілька одиниць (в кілька разів), задачі на різницеві та кратне порівняння чисел; та складені задачі на 3 – 4 дії; - розв’язувати складені задачі, в яких використовується залежність між величинами (швидкістю, часом і відстанню при рівномірному прямолінійному русі; ціною, кількістю і вартістю товару; площею прямокутника і довжинами суміжних сторін); - розпізнавати і зображати (на папері в клітинку за допомогою циркуля і лінійки) геометричні фігури – точку, відрізок, промінь, пряму, ламану, кут, коло, круг, квадрат, прямокутник, трикутник; - вимірювати довжину відрізка, довжину ламаної; - креслити відрізок заданої довжини; - обчислювати периметр многокутників; площу прямокутника і квадрата.
В даному посібнику розглянемо методику вивчення окремих тем курсу математики 4-го класу: методику узагальнення і систематизації знань учнів на початку навчального року; методику вивчення усної і письмової нумерації багатоцифрових чисел; додавання і віднімання багатоцифрових чисел; множення і ділення на одно- та двоцифрові числа. А також, запропонуємо методику введення окремих видів задач, методику ознайомлення з рівняннями ускладненої структури; розглянемо задачі з геометричним змістом; приділимо увагу вивченню величин і розв’язуванню нестандартних задач.
Узагальнення та систематизація знань за третій клас.
Нумерація трицифрових чисел
Кожний учень, який починає навчатися у 4-му класі повинен правильно називати та записувати двоцифрові та трицифрові числа. Цьому сприяє вивчення десяткової позиційної системи зчислення, в якій використовуються 10 знаків (цифр): 0,1,2,3,4,5,6,7,8,9 та розрядні одиниці: 1, 10, 100, 1000... Так трицифрове число 872 можна подати у вигляді: 872 = 800 + 70 + 2 або 872 = 8 * 100 + 7 * 10 + 2 В запису цього числа, крім цифр, за допомогою яких воно записано, беруть участь розряди одиниць, десятків, сотень, які в купі складають перший клас – клас одиниць. Такий запис числа називають розкладом на розрядні доданки (або розрядні одиниці). Учень повинен вміти записувати будь-яке трицифрове число у вигляді суми розрядних доданків (або одиниць): 506 = 500 + 6 або 506 = 5 * 100 + 0 * 10 + 6 980 = 900 + 80 або 980 = 9 * 100 + 8 * 10 + 0 а також вміти визначати числа, які подані у вигляді суми розрядних одиниць (або доданків): 400 + 30 + 7 = 437 або 4 * 100 + 3 * 10 + 7 = 437 600 + 1 = 601 або 6 * 100 + 0 * 10 + 1 = 601 Запис числа у вигляді суми розрядних доданків може бути використаним при розв’язуванні більш складних задач, в яких треба вміти записати загальний вигляд двоцифрового та трицифрового числа. Так,
Розглянемо декілька задач. Задача 1. Дано двоцифрове число, у якого цифра десятків дорівнює 3. Якщо до нього додати двоцифрове число, у якого цифра десятків збільшена у 2 рази, а цифра одиниць залишилася без зміни, то одержимо число 94. Яке двоцифрове число було дано? Розв’язання. Дане двоцифрове число можна записати у вигляді: Додамо до першого числа друге число і за умовою задачі одержимо число 94.
(30 + 60) + (а + а) = 94 90 + а* 2 = 94 а * 2 = 94 – 90 а * 2 = 4 а = 4: 2 а = 2 Отже, дане число складається з 3-х десятків і 2-х одиниць. Це число 32. Задача 2. Скільки різних двоцифрових чисел можна записати за допомогою цифр 1,5. Розв’язання. Це можуть бути такі числа: 11, 15, 51, 55. Перші два числа мають однакову цифру десятків: 1; останні два числа також мають однакову цифру десятків: 5. Ці числа попарно відрізняються лише цифрою одиниць. - Яке серед цих чисел найбільше? Найменше? (55, 11) - У скільки разів найбільше число більше за найменше? (В 5 разів) - Числа 11 та 55 записані однаковими цифрами. Чи буде їх сума або різниця також записані однаковими цифрами? (Так: 55 + 11 = 66, 55 – 11 = 44) - У скільки разів їх сума (різниця) більша, чим найменше число? (В 6 разів, в 4 рази) - Про числа 15 та 51 кажуть, що вони записані однаковими цифрами, але в оберненому порядку. Число 15 ділиться на 3.Чи ділиться на 3 число 51? Так, число ділиться на 3, якщо сума його цифр ділиться на 3! - Число 15 ділиться на 5. Чи ділиться на 5 число 51? Ні, щоб число ділилося на 5, воно повинно закінчуватися цифрою 5! - Чи вірним буде висновок: а) якщо двоцифрове число ділиться на 3, то двоцифрове число, записане тими самими цифрами, але в оберненому порядку, також ділиться на 3? б) якщо двоцифрове число ділиться на 5, то двоцифрове число записане тими самими цифрами, але в оберненому порядку, не ділиться на 5? - Знайдіть суму цих чотирьох чисел: 11, 15, 51,55. Як це зробити зручніше? 11 + 15 + 51 + 55 = (11 + 55) + (15 + 51) = 66 + 66 = 132 - Чи ділиться одержана сума на 3? (Так.) Чи ділиться на 3 кожний з доданків (Ні) Який висновок можна зробити? Якщо кожний доданок ділиться на 3, то їх сума ділиться на 3. Якщо сума кількох доданків ділиться на 3, то не обов’язково, що кожний з доданків ділиться на 3. Задача 3. Дано цифрі 1, 4, 5. Скільки трицифрових чисел можна записати за допомогою цих цифр так, щоб вони не повторювалися в записі числа? Розв’язок. Цифрою сотень шуканих чисел може бути 1 або 4 або 5. Якщо цифра сотень 1, то маємо: 145 та 154. Міркуючи так само на випадок, коли цифра сотень дорівнює 4 або 5, одержимо всі трицифрові числа: 145 415 514 154 451 541 Таких чисел всього 6. - Скільки серед них парних? Чому? - Скільки серед них непарних? - Скільки серед них таких, які діляться на 5? Чому? - Розглянемо непарні числа серед записаних, що мають однакову цифру одиниць. Це: 451 та 541; 145 та 415. Чому дорівнюють їх суми? 451 + 541 = 992 145 + 415 = 560 - Чи ділиться кожна з цих сум на 3? Чому? - Чи вірно твердження: якщо кожний доданок не ділиться на 3, то і сума цих доданків не ділиться на 3? (Ні.) Наведіть приклад: кожний з двох доданків не ділиться на 3, а їх сума ділиться на 3. - Знайдемо різницю цих чисел. 541 – 451 = 90 415 – 145 = 270 - Чи ділиться кожна з одержаних різниць на 3? (Так.) Проте ні зменшуване, ні від’ємник не діляться на 3. Отже запам’ятайте: якщо різниця двох чисел ділиться на 3, то це не означає, що зменшуване і від’ємник також діляться на 3. Наведіть відповідний приклад. Таким чином, ми узагальнили поняття позиційної системи зчислення для трицифрового числа; назви розрядів, розрядні одиниці; запис числа у вигляді суми розрядних доданків та заміну суми розрядних доданків числом; на підставі цих знань запропонували розв’язати задачі. Лишилося повторити порівняння трицифрових чисел, визначення загальної кількості сотень, десятків та одиниць в числі, а також обчислювальні прийоми додавання і віднімання на підставі нумерації.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.71.13 (0.007 с.) |

 = 10а + в – загальний вигляд двоцифрового числа, де а – цифра десятків, в – цифра одиниць, запис ав – це не добуток, а два знаки, записані підряд, тобто запис двоцифрового числа.
= 10а + в – загальний вигляд двоцифрового числа, де а – цифра десятків, в – цифра одиниць, запис ав – це не добуток, а два знаки, записані підряд, тобто запис двоцифрового числа.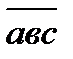 = 100а + 10в + с – загальний вигляд трицифрового числа, де а – цифра сотень, в – цифра десятків, с – цифра одиниць.
= 100а + 10в + с – загальний вигляд трицифрового числа, де а – цифра сотень, в – цифра десятків, с – цифра одиниць. – це двоцифрове число, яке записано тими самими цифрами, що й число
– це двоцифрове число, яке записано тими самими цифрами, що й число  , але в оберненому порядку.
, але в оберненому порядку. – це трицифрове число, яке записано такими самими цифрами, що й число
– це трицифрове число, яке записано такими самими цифрами, що й число  = 30 + а, в цьому числі 3 – цифра десятків, а – цифра одиниць. Збільшимо цифру десятків у 2 рази, не змінюючи цифру одиниць, одержимо число:
= 30 + а, в цьому числі 3 – цифра десятків, а – цифра одиниць. Збільшимо цифру десятків у 2 рази, не змінюючи цифру одиниць, одержимо число:  = 60 + а.
= 60 + а. = 94 або 30 + а + 60 + а = 94
= 94 або 30 + а + 60 + а = 94


