
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Арифметичні дії додавання і віднімання, множення і діленняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Учням відомі чотири арифметичні дії: додавання і віднімання – це дії першого ступеню, множення і ділення – дії другого ступеню. Більше число на першому ступені знаходять дією додавання, а на другому – множенням. Отже множення – це аналог дії додавання на другому ступені. Множення – це додавання однакових доданків. Оберненою до дії додавання є дія віднімання. - Що означає від числа 14 відняти 7? (Із 14 відняти 7 – це означає знайти таке число, яке в сумі з числом 7 дає 14.)
14 – 7 = 7, тому що 7 + 7 = 14 + Оберненою до дії множення є дія ділення. - Що означає число 14 розділити на 7? (14 розділити на 7 – це означає знайти таке число, яке у добутку з числом 7 дає число 14.) 14: 7 = 2, тому що 2 * 7 = 14 * При додаванні числа, які додають називають однаково – доданками, і при множенні – теж однаково, множниками. Результат дії додавання називається сумою, а дії множення – добутком. - Що спільного у назвах компонентів дій додавання і множення? (Компоненти дії додавання та множення називаються однаково, але відрізняються порядком: перший При відніманні число, від якого віднімають, зменшується, тому воно й називається зменшуване; число, яке віднімають, називають від’ємником. При діленні число, яке ділять називають діленим, а число на яке ділять, називають дільником. Результат дії віднімання називають різницею, а результат дії ділення – часткою. - Що спільного у назвах компонентів дій віднімання і ділення? (Компоненти дій віднімання і ділення називаються по різному: - Як пов’язані між собою дії віднімання і додавання? Ділення і множення?
Це зручно показати, використовуючи букви, тобто розглядаючи буквені вирази. Якщо а – в = с, то а = в + с І навпаки, якщо а = в + с, то а – в = с або а – с = в Якщо а: в = с, то а = в * с І навпаки, якщо а = в * с, то а: в = с або а: с = в - Чи завжди можна виконати дію додавання у множині натуральних чисел? (Так. Завжди можна знайти таке натуральне число, що є сумою двох інших натуральних чисел.) Наведіть приклади. - Чи завжди у множині натуральних чисел можна виконати дію множення? (Так.. Завжди можна знайти таке натуральне число, що є добутком двох інших натуральних чисел.) Наведіть приклади. - Чи завжди у множині натуральних чисел можна виконати дію віднімання? (Дію віднімання не можна виконати, якщо зменшуване менше за від’ємник.) Наведіть приклади.
- Чи завжди у множині натуральних чисел можна виконати дію ділення націло? (Ні, не завжди можна знайти таке натуральне число, що при множенні на дільник дає ділене. Крім того, ділене повинно бути не меншим за дільник.) Наведіть приклади. Якщо а = в * с, то кажуть, що число а ділиться на в, при цьому часткою є число с. Подалі ми будемо казати і так: а кратне в (це одне й те саме, що й а ділиться в.). Так, 21 кратне 7, 63 кратне 9 і так далі. - Яке число ми отримаємо, якщо до даного числа додамо 1? (Ми отримаємо наступне число.) Яке число ми отримаємо, що дане число помножимо на 1? (Ми отримаємо те саме число.)
- Яке число ми отримаємо, якщо до даного числа додамо нуль? (Отримаємо те саме число.) Яке число ми отримаємо, коли дане число помножимо на 0? (Ми отримаємо нуль!)
- В якому випадку сума дорівнюватиме одному з доданків? (Коли інший доданок 0!) В якому випадку добуток дорівнюватиме одному з множників? (Коли інший множник 1!)
- Яке число ми отримаємо при відніманні однакових чисел? (При відніманні однакових чисел ми отримаємо 0.) Яке число ми отримаємо при діленні однакових чисел? (При діленні однакових чисел ми отримаємо 1.)
- Яке число отримаємо при відніманні 1? (При відніманні 1 з даного числа отримаємо попереднє число.) Яке число отримаємо при діленні на 1? (При діленні на 1 отримаємо те саме число.)
- Яке число отримаємо при відніманні 0? (При відніманні 0 із даного числа, отримаємо те саме число.) Чи можна ділити на нуль? (На нуль ділити не можна, тому що не існує такого числа, яке при множенні на нуль дає число, відмітне від нуля.) Яке число отримаємо при діленні нуля на будь-яке число? (При діленні нуля на будь-яке число отримаємо нуль.)
- В якому випадку різниця дорівнюватиме зменшуваному? (Якщо від’ємник дорівнюватиме нулю.) Всякому випадку частка дорівнюватиме діленому? (Якщо дільник дорівнює 1.)
- В якому випадку різниця дорівнюватиме нулю? (Якщо від’ємник дорівнює зменшуваному.) В якому випадку частка дорівнюватиме нулю? (Якщо ділене 0.)
- Для яких арифметичних дій виконується переставний закон? Сформулюйте переставний закон додавання (множення).
а + в = в + а а * в = в * а Завдання 1. Обчислити зручним способом: 12 + 24 + 8 2 * 7 * 5 160 + 70 + 140 50 * 9 * 2 25 * 7 * 4 17 + 56 + 23 4 * 9 * 5 420 + 275 + 80
- Сформулюйте сполучний закон додавання. Як додати число до суми? Сформулюйте сполучний закон множення. Як помножити добуток на число?
- Як додати суму до числа? Як помножити число на добуток?
- Які закони або властивості застосовані для наступних обчислень? 43 + 29 = 43 + (20 + 9) = (43 + 20) + 9 = 63 + 9 = 72 43 + 29 = 43 + (7 + 22) = (43 + 7) + 22 = 50 + 22 = 72 5 * 14 = 5 * (2 * 7) = (5 * 2) * 7 = 10 * 7 = 70 - Як можна інакше обчислити добуток чисел 5 та 14? На підставі застосування якого правила? 5 * 14 = 5 * (10 + 4) = 5 * 10 + 5 * 4 = 50 + 20 = 70 - Сформулюйте правило множення суми на число. Це розподільний закон множення відносно додавання. - Сформулюйте правило ділення суми на число. Це розподільний закон ділення відносно додавання.
В яких випадках обчислення ми застосовуємо правило множення суми на число? (При множенні двоцифрового числа на одноцифрове.) Наведіть приклади. - В яких випадках ми застосовуємо правило ділення суми на число? (При діленні двоцифрового числа на одноцифрове.) Завдання 2. Розв’яжіть приклади: 23 * 4 42: 3 16 * 7 84: 7 69: 3 72 * 2 - Як можна міркувати при діленні двоцифрового на двоцифрове число? (Можна добирати таке число, яке у добутку з дільником дає ділене, а можна замінити дільник добутком і послідовно поділити на кожний множник.) - Розгляньте, як знайшли частку чисел 64 та 16. 64: 16 = 64: (8 * 2) = (64: 8): 2 = 8: 2 = 4 - Яким правилом користувалися при розв’язанні? (Користувалися правилом ділення числа на добуток.) Порівняйте правила множення числа на добуток з правилом ділення числа на добуток.
- Що спільного в цих правилах? Що відмітного? (Спільне те, що спочатку множать або ділять на один множник, а потім множать або ділять на інший множник.) Опорний конспект 1.
Означення:
Задачі на конкретний зміст арифметичних дій:
Назва компонентів і результату дії:
Перевірка:
Взаємозв'язок арифметичних дій:
Властивості:
Переставний закон:
Сполучна закон:
Розподільний закон:
Зауважимо, що розподільний закон додавання відносно множення місця не має. Опорний конспект 2
Означення:
Задачі на конкретний зміст арифметичних дій:
Назва компонентів і результату дії:
Перевірка:
Взаємозв'язок арифметичних дій:
Правила:
Розподільний закон
Треба зазначити, що 4-й клас є випускним класом початкової школи, тому одним із завдань, що стоїть перед вчителем, є підготовка учнів до вивчення математики у середній школі. В 5-му класі у чинному підручнику, автором якого є Г.М.Возняк, Г.М.Литвиненко, М.П. Маланюк (Київ “Освіта”, 1998), учням пропонується багато завдань на застосування знань про зміну результатів арифметичних дій при зміні їх компонентів. Ці знання згідно попередньої програми не були окремим питанням початкового курсу математики, а за новою програмою, авторами якої є Л. Кочина та Н.Листопад, передбачено вивчення залежності між компонентами та результатами арифметичних дій додавання і віднімання, але вивчення залежності між компонентами та результатами арифметичних дій множення і ділення не зазначено у програмі. Таким чином, виходячи з діючої програми та вимог наступного навчання, знанням про зміну результатів арифметичних дій при зміні їх компонентів слід приділити певну увагу.
Зміна результатів арифметичних дій при зміні компонентів (ЗРАДПЗК) – один із видів завдань, які повинні виконувати учні при вивченні кожної арифметичної дії. Учні повинні знати як зміниться результат якої-небудь арифметичної дії, якщо змінити один з її компонентів або два компонента; або як треба змінити компоненти, щоб результат не змінився. Ці знання мають вагоме значення для формування у дітей первісних уявлень про функціональну залежність. Зазначимо, що лінія функції – одна із ведучих ліній шкільного курсу математики взагалі, тому дуже важливо, щоб вже в початкових класах учні накопичували функціональні уявлення.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.163.23 (0.014 с.) |

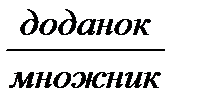 , другий
, другий 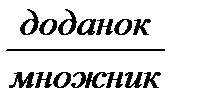 .)
.)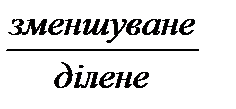 ,
, 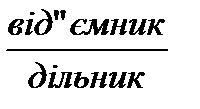
 .)
.)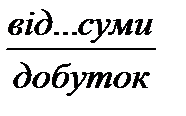 двох чисел
двох чисел 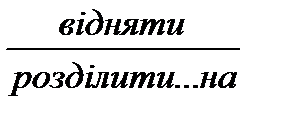 один
один 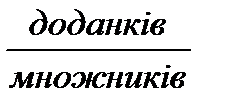 значення
значення 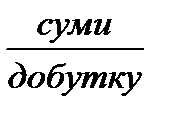 не змінюється.
не змінюється.
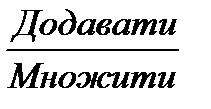 числа можна у будь-якому порядку.
числа можна у будь-якому порядку.

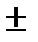 в) * с = а * с
в) * с = а * с 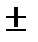 в): с = а: с
в): с = а: с 


