
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі, що утримують величини: швидкість, час, відстань.Содержание книги
Поиск на нашем сайте 1. Ознайомлення учнів з поняттям про швидкість. Ознайомлення з взаємозв’язком між швидкістю, часом та відстанню при рівномірному русі. Підготовча робота. Мета – узагальнення знань дітей про рух тіл. На цьому етапі пропонуємо учням: - Екскурсії по спостереженню за рухом транспорту, пішоходів (Діти помічають, що одне тіло рухається швидше, а інше - повільніше.). - Спостерігання в умовах класу, де рух демонструють самі діти – рух двох тіл відносно одне одного (Двоє учнів починають рухатися одночасно в одному напрямі: заздалегідь зазначається час руху або відстань, яку повинні подолати учні). Ознайомлення. Діти вже знайомі з величинами: час та відстань. Чули вони й слово „швидкість”. Але, перед тим, як перейти до розгляду залежності між відстанню, швидкістю та часом при рівномірному русі, поняття про швидкість руху треба ввести. Спостерігаючи за рухом кількох тіл, учні помітили, що: - за один й той самий час два тіла можуть пройти різну відстань; - одну й ту саму відстань два тіла можуть подолати за різний час. Чому так відбувається? Учні можуть відповісти: „Тому що у цих тіл різні швидкості!”. Що таке швидкість? На це запитання навряд можна отримати свідому відповідь... Поняття про швидкість вводиться на задачі. Задача. За 3 години хлопчик проїхав на велосипеді 24 км, кожного часу проїжджаючи однакову відстань. Скільки кілометрів проїздив хлопчик у кожний час? - Про що розповідається в задачі? (Про рух велосипедиста. Відомо, що він проїхав 24 км.) 24 км всього проїхав велосипедист – це загальна відстань. Що ще відомо? (Велосипедист рухався 3 години. В годинах вимірюється час. 3 години – це час руху велосипедиста.) - Схематично проілюструємо умову задачі: накреслимо відрізок, який позначає загальну відстань – 24 км. Велосипедист подолав цю відстань за 3 години, проїжджаючи однакову відстань кожної години, тому цю відстань поділимо на 3 рівні частини; кожна частина ілюструє відстань, яку долав велосипедист за 1 годину. Виконаємо зміні у попередньому кресленні. ?
24 км - Запишімо задачу коротко у формі таблиці:
- Якою дією дізнаємося про відстань, яку подолав велосипедист за 1 годину? (Дією ділення, треба 24 км поділити порівну на 3 рівні частини.) Розв’язання 24: 3 = 8 (км) відстань за 1 годину. Відповідь: по 8 км проїздив велосипедист за кожну годину. - Відстань, яку проїздив велосипедист за кожну годину є швидкістю руху велосипедиста.
- Отже швидкість руху велосипедиста – 8 км за годину. Скорочено це записується так: 8 - Що ми знайшли в задачі? (Швидкість) Звернемося до розв’язання задачі. Що означає число 24? (Це відстань, яку подолав велосипедист.) Що означає число 3? (Це час руху.) Що ми знайшли в задачі? (Швидкість) Як ми знайшли швидкість? (Ми відстань поділили на час.) - Зробіть висновок про те, як знайти швидкість.
Вводимо правило знаходження швидкості до загального „своду” відношень пропорційних величин:
Зауваження. В задачах на рух звичайно вважають, що швидкість тіла протягом всього часу руху не змінюється. Такий рух називається рівномірним. Закріплення правила знаходження швидкості. Далі треба обговорити питання: 1. Що означає, що: - равлик повзе зі швидкістю 6 - літак летить зі швидкістю 950 - легкова машина їде зі швидкістю 120 - пліт пливе по річці зі швидкістю 4 - швидкість велосипедиста 18 - швидкість лижника 200 - швидкість пароплаву 45 - Земля рухається по орбіті зі швидкістю 30 - черепаха повезе зі швидкістю 3 - ластівка летить зі швидкістю а 2. Чому дорівнює швидкість руху: - пішоходу, якщо він проходить 5 км за 1 годину? (5 - меч-риби, якщо вона кожного часу пропливає 100 км? (100 - бджоли, якщо вона за кожну секунду пролітає 7 м? (7 - верблюда, якщо він в кожний час проходить 35 км? (35 - космічного корабля, якщо він у кожну секунду долає 8 км? (8 - поїзду, якщо він проїжджає за кожну хвилину 15 км? (15 - літака, якщо він за годину, пролетів 870 км? (870 - лижника, якщо він за хвилину пройшов в м? (в 3. Розв’яжи задачі: - За 9 годин машина проїхала 747 км. Скільки кілометрів вона проїжджала за 1 годину? Яка швидкість автомобіля? - Бігун пробіг 300 м за 50 с. Скільки метрів він долав за 1 секунду? З якою швидкістю біг бігун? При розв’язанні цих задач корисно звернути увагу учнів на те, що вони містять не два запитання, а одне, яке сформульовано по-різному. Задача. За даними таблиці обчисли швидкість руху велосипедиста, вантажного автомобіля, ластівки, пасажирського літака.
Робота над цим завданням здійснюється за планом: 1. Назвіть відстань, яку подолало тіло. 2. Назвіть час руху цього тіла. 3. Як знаючи відстань і час руху знайти швидкість? 4. Знайдіть швидкість тіла
Для усвідомлення залежності швидкості, відстані та часу, учням пропонуються для порівняння пари задач: 1) Пішохід за 4 години пройшов 20 км. Знайдіть швидкість пішоходу. 2) Лижник за 4 години подолав 60 км. Знайдіть швидкість лижника. Після розв’язання і порівняння цих двох задач пропонуємо учням запитання: - Чия швидкість більша? (Лижника.) - Чому швидкість лижника більша за швидкість пішоходу? (Швидкість лижника більша, тому що він за один й той самий час, що й пішохід, подолав більшу відстань.) - Який висновок можна зробити про залежність між швидкістю і шляхом? (Чим більша швидкість, тим більший шлях долає тіло за один й той самий час.) - Отже, швидкість і відстань змінюється в однаковому напрямі, якщо час залишається сталим. - Як зміниться відстань, якщо швидкість збільшиться? Зменшиться? - Як зміниться швидкість, якщо відстань збільшиться? Зменшиться? 3) Лижник пройшов 45 км за 3 години. Яка швидкість лижника? 4) Пішохід пройшов 45 км за 9 годин. Яка швидкість пішоходу? - Чия швидкість більша? (Лижника.) - Чому швидкість лижника більша за швидкість пішоходу? (Швидкість лижника більша, тому що він одну й ту саму відстань, що й пішохід, пройшов за менший час.) - Який висновок можна зробити про залежність між швидкістю і часом? (Чим більша швидкість, тим менший час потрібний для подолання одного й того самого шляху.) - Отже, швидкість і час змінюються в оберненому напрямі: якщо швидкість збільшується, то час, навпаки, зменшується; якщо швидкість зменшується – то час збільшується, при сталій відстані. - Як зміниться час, якщо швидкість збільшиться? Зменшиться? - Як зміниться швидкість, якщо час збільшиться? Зменшиться?
Треба зазначити, що в чинному підручнику математики для 5-го класу, автором якого є Г.М.Возняк та інші, тема „Швидкість” не пропонується, але є дуже багато вправ на переклад одних одиниць вимірювання величини у інші, в тому числі і переклад одиниць швидкості. Отже, для попередження труднощів при вивченні математики в 5-му класі і для повноцінного формування поняття про швидкість, як про шлях, що долає тіло за одиницю часу, корисними є завдання на переклад одних одиниць вимірювання швидкості в інші: 1) 5 Розв’язання 5
2) 48 Розв’язання Перша частина міркування така сама, як і міркування в попередній задачі. Маємо 48 Далі міркуємо так: 48000
3) 18 Розв’язання Міркуючи аналогічно, попереднім двом задачам, маємо: 18 18000 300
4) 7 Розв’язання 7
5) 3000 Розв’язання 3000
Після усвідомлення учнями процесу перекладу одних одиниць вимірювання швидкості в інші, можна запропонувати задачі: 1) Космічний корабель рухається зі швидкістю 8 Розв’язання 8 2) Пішохід проходить за 1 годину 3 км. Скільки метрів він проходить за 1 хвилину? Знайдіть його швидкість у Розв’язання. Пішохід проходить за 1 годину 3 км. В 1 км – 1000 м. Тому за 1 годину він проходить: 3 * 1000 = 3000 м. Треба дізнатися, скільки метрів він проходить за 1 хвилину. 1 хвилина у 60 разів менша за годину. Тому пішохід пройде відстань за 1 хвилину у 60 разів меншу: 3000: 60 = 50
2. Методика введення правила знаходження відстані за відомими швидкістю та часом.
Задача. Лижник був у дорозі 3 год., рухаючись зі швидкістю 12 - Про що розповідається в задачі? (Про рух лижника. Відомо, що він йшов зі швидкістю 12 - Яку відстань пройшов лижник за першу годину? (12 км.) - За другу годину? (12 км) За третю годину? (12 км.) - Схематично проілюструємо умову задачі. 12 км 12 км 12 км
? км - Запишемо задачу коротко у формі таблиці таблиці:
- Якою дією дізнаємося про загальну відстань, яку подолав велосипедист за 3 години? (Дією множення, треба по 12 км взяти 3 рази.) Розв’язання 12 * 3 = 36 (км) Відповідь: 36 км подолав лижник за 3 години. - Звернемося до розв’язання задачі. Що означає число 12? (Це швидкість лижника.) Що означає число 3? (Це час руху.) Що ми знайшли в задачі? (Відстань) Як ми знайшли відстань? (Ми швидкість помножили на час.) - Зробіть висновок про те, як знайти відстань.
Для закріплення правила пропонується завдання, в якому за даними таблиці слід знайти відстані. Робота над цим завданням: - Що відомо про рухомий об’єкт? (Швидкість.... Час...) - Що треба знати? (Відстань.) - Як знайти відстань? (Щоб знайти відстань, треба швидкість помножити на час.) - Обчисліть відстань.
3. Методика введення правила знаходження часу за відомими відстанню та швидкістю руху.
Задача. Пасажир проїхав автобусом 180 км. Швидкість автобуса 60 - Про що розповідається в задачі? (Про рух автобусу. Відомо, що автобус проїхав 180 км зі швидкістю 60 - Яку відстань проїхав автобус за першу годину? (60 км.) - Чи всю відстань він подолав? (Ні.) - За другу годину? (60 км) Чи всю відстань він подолав? - За третю годину? (60 км.) Чи всю відстань він подолав? (Так.) 60 км 60 км 60 км
180 км - Отже, автобус витратив на рух стільки годин, скільки в 180 км міститься по 60 км. - Запишемо задачу коротко у формі таблиці:
- Якою дією дізнаємося про час руху автобусу? (Годин буде стільки, скільки разів міститься в 180 км по 60 км, щоб це дізнатися треба 180 км поділити по 60 км.) Розв’язання 180: 60 = 3 години. Відповідь: 3 години пасажир їхав автобусом. - Звернемося до розв’язання задачі. Що означає число 180? (Це відстань, яку проїхав автобус.) Що означає число 60? (Це швидкість автобуса.) Що ми знайшли в задачі? (Час) Як ми знайшли час? (Ми відстань поділили на швидкість.) - Зробіть висновок про те, як знайти час.
4. Формування умінь розв’язувати прості задачі з величинами: відстань, швидкість та час.
Спочатку слід узагальнити спосіб отримання формул швидкості та часу з формули відстані.
Для закріплення зробленого узагальнення корисні вправи типу: 1. Використовуючи формулу відстані S = V * t, заповни таблицю:
2. Розв’яжи задачу. Склади обернені задачі і розв’яжи їх. Вершник їде зі швидкістю 8 Отже, маємо три взаємно обернені задачі:
3. Порівняй задачі: 1) Чому дорівнює швидкість поштового голуба, якщо він за 3 години пролітає 180 км? 2) Чому дорівнює швидкість бджоли, якщо вона за 3 години пролітає 60 км? - Що в них спільного? (Однаковий час – 3 години.) - Чим вони відрізняються? (Різна відстань: голуб пролетів 180 км, а бджола – 60 км). - Як ви вважаєте, у кого буде швидкість більшою? Чому? (У голуба, тому що він за один й той самий час пролетів більшу відстань. Швидкість і відстань змінюються в одному напрямі!) - Розв’яжіть задачі і перевірте власне передбачення. - Порівняйте відстані. У скільки разів голуб пролетів більшу відстань? - Порівняйте швидкості. У скільки разів швидкість голуба більша? - Який висновок можна зробити? (Якщо відстань збільшити в 3 рази, то й швидкість, теж збільшиться в 3 рази.) - Як ви вважаєте, як зміниться швидкість, якщо відстань зменшиться в 3 рази? (Швидкість теж зменшиться в 3 рази. Для того, щоб в цьому впевнитися слід порівняти відстань бджоли і голуба; швидкість бджоли і голуба!) 4. Порівняй задачі: 1) Підводний човен проплив 180 км за 3 години. Знайди швидкість підводного човна. 2) Пароплав проплив 180 км за 6 годин. Знайди швидкість пароплаву. - Що в них спільного? (Однакова відстань – 180 км.) - Чим вони відрізняються? (Різний час: підводний човен плив 3 години, а пароплав – 6 годин.). - Як ви вважаєте, у кого буде швидкість більшою? Чому? (У підводного човна, тому що він одну й ту саму відстань подолав за менший час. Швидкість і час змінюються в протилежних напрямах!) - Розв’яжіть задачі і перевірте власне передбачення. - Порівняйте відстані. У скільки разів менше витратив часу підводний човен? - Порівняйте швидкості. У скільки разів швидкість підводного човна більше? - Який висновок можна зробити? (Якщо час зменшити в 2 рази, то й швидкість, навпаки, збільшиться в 2 рази.) - Як ви вважаєте, як зміниться швидкість, якщо час збільшити в 2 рази? (Швидкість, навпаки, зменшиться в 2 рази.) 5. Порівняй задачі: 1) За скільки годин проїде відстань 720 км „Мерседес”, якщо їхатиме зі швидкістю 180 2) За скільки годин проїде відстань 720 км „Лада”, якщо їхатиме зі швидкістю 90 - Що в них спільного? (Однакова відстань – 720 км.) - Чим вони відрізняються? (Різна швидкість: швидкість „Мерседесу” – 180 - Як ви вважаєте, яка машина витратить на дорогу менше часу? Чому? (Менше часу витратить „Мерседес”, тому що одну й ту саму відстань (720 км) він долає з більшою швидкістю. Час і швидкість змінюються в протилежних напрямах!) - Розв’яжіть задачі і перевірте власне передбачення. - Порівняйте швидкості. У скільки разів більше швидкість „Мерседесу”? - Порівняйте час руху. У скільки разів час руху „Мерседесу” менше? - Який висновок можна зробити? (Якщо швидкість збільшити в 2 рази, то й час, навпаки, зменшиться в 2 рази.) - Як ви вважаєте, як зміниться час, якщо швидкість зменшити в 2 рази? (Час, навпаки, збільшиться в 2 рази.) 6. Порівняй задачі: 1) За який час машина, яка їде зі швидкістю 80 2) За який час машина, яка їде зі швидкістю 80 Висновок: при однаковій швидкості, час і відстань змінюються в одному напрямі; якщо відстань збільшиться (зменшиться) в 3 рази, то й час. Так само, збільшиться (зменшиться) в 3 рази. 4. Лижник біг зі швидкістю 28 - Що незвичайного в цій задачі? (Швидкість подана у - Як ми міркували у попередній задачі? (Ми подали час у одиницях, які відповідають одиниці швидкості.) - Подайте 15 хвилин у годинах. (15 хвилин = - Що означає швидкість лижника 28 - А за 5. Машина їде зі швидкістю 120 - Згадайте формулу часу. - Що треба знати, щоб знайти час? (Треба знати два числові значення: відстань, відомо – 10 км; та швидкість, відомо – 120 - Чи можна відразу відповісти на запитання задачі? (Ні. Ми не можемо 10 поділити на 120.) - Що означає швидкість машини 120 - А 10 км, вона проїде більше чи менше, ніж за годину? (10 км машина проїде, менше, ніж за годину. Тому швидкість треба подати у інших одиницях – в - Машина за кожну годину проїжджає по 120 км; 120 км вона проїжджає за 60 хвилин. А скільки кілометрів проїжджає машина за 1 хвилину? (120: 60 = 2 км за 1 хвилину. Отже швидкість машини 2 - Розв’яжіть задачу і дайте відповідь на її запитання. 6. Велосипедист їде зі швидкістю 14 - Порівняйте цю задачу з попередньою. Чим вони відрізняються? Що в них спільного? - Чи можна цю задачу розв’язувати так само, як і попередню задачу? (Ні, ми не зможемо швидкість 14 - Як можна міркувати в цій задачі? 14 км проїжджає велосипедист за 1 годину, а 7 км він проїде більше чи менше, ніж за 1 годину? (Менше.) У скільки разів менше? (У стільки, у скільки 7 км менше, ніж 14 км: 14: 7 = 2 – у 2 рази менше витратить часу машина на 7 км, ніж на 14 км. На 14 км машина витратила 1 годину, тому на 7 км – 1 год.: 2 = 7. Людина йде зі швидкістю 4 - Порівняйте цю задачу з № 12. Чим вони схожі? Чи можна цю задачу розв’язати так само? (Ні, ми не можемо дізнатися у скільки разів 3 км менше, ніж 4 км; 4 на 3 націло не ділиться.) - Порівняйте цю задачу з задачею № 11. Чим вони схожі? Чи можна її розв’язати так само? (Ні, ми не зможемо дізнатися скільки кілометрів людина проходить за 1 хвилину; 4 на 60 не ділиться.) - Що означає швидкість 4 - А скільки часу потрібно людині, щоб пройти 1 км? (60: 4 = 15 хвилин потрібно людині, для того, щоб пройти 1 км.) - Скільки хвилин потрібно людині, щоб пройти 3 км? (У 3 рази більше: 15 * 3 = 45 хвилин.)
Задачі на час. Задачі на час містять три компоненти: дата початку події, тривалість події і дата закінчення події. Ці задачі записуються коротко в формі таблиці:
В 3-му класі такі задачі розв’язувалися з застосуванням циферблату годинники або табель-календаря, а в 4-му класі – обчисленням. Міркування здійснюються за правилами:
Певні труднощі викликають у дітей задачі: Задача 1. Учні виїхали на екскурсію 7 серпня о 10 год ранку, а повернулися 15 серпня о 8 год вечора. Скільки часу вони пробули на екскурсії?
Треба визначити, який проміжок часу відповідає даті 7 серпня 10 год ранку: від початку серпня до 7 числа пройшло 6 повних діб, 10 год ранку – це означає, що від початку доби пройшло 10 годин. Маємо: 6 діб 10 год. Визначимо, який проміжок часу відповідає даті 15 серпня 8 год вечора: від початку серпня до 15 числа пройшло 14 повних діб, від початку доби до 8 год вечора пройшло 20 год. Маємо: 14 діб 20 год.
Задача 2. Перший у світі штучний супутник Землі запису тили 4 жовтня 1957 року, третій супутник – 15 травня 1958 року. Скільки минуло часу від запуску першого до запуску третього супутника?
Треба визначити, який проміжок часу відповідає даті 4 жовтня 1957 р: від початку літочислення до 1957 р минуло 1956 повних років; від початку року до жовтня місяця минуло 9 повних місяців; від початку жовтня до 4 числа минуло 3 повні доби. Маємо: 1956 р 9 міс 3 доби. Треба визначити, який проміжок часу відповідає даті 15 травня 1958 року: від початку літочислення до 1958 року минуло 1957 повних років; від початку року до травня місяця минуло 4 повні місяці; від початку травня до 15 число минуло 14 повних діб. Маємо 1957 р 4 міс 14 діб.
Також пропонуються задачі на знаходження площі прямокутника і задачі на знаходження невідомої стороні за площею прямокутника та іншою стороною. Ці задачі ми розглянемо у розділі „Величини в курсі 4-го класу”.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1792; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

 .
. Одиниці вимірювання швидкості:
Одиниці вимірювання швидкості:  й тощо.
й тощо.
 ? (Швидкість равлика 6
? (Швидкість равлика 6  ?
? )
) )
) )
)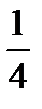 год.)
год.) години, лижник пробіжить більшу чи меншу відстань? (Меншу, у 4 рази: 28: 4 = 7 км – пробіжить лижник.)
години, лижник пробіжить більшу чи меншу відстань? (Меншу, у 4 рази: 28: 4 = 7 км – пробіжить лижник.) год..)
год..)


