
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі на одночасний рух в різних напрямкахСодержание книги
Поиск на нашем сайте
Особливий тип задач, які містять опис процесу руху двох тіл, які переміщуються в одному або в різних напрямках, називають задачами на рух. Задачі на рух містять пропорційні величини: відстань, швидкість та час. Кожна з цих задач має три види в залежності від даних та шуканого: 1 вид – задачі на знаходження відстані: дано швидкості обох тіл та час їх спільного руху, треба знайти відстань; П вид – задачі на знаходження швидкості: дано відстані, які подолані обома тілами, відомий час їх спільного руху та швидкість одного з тіл, треба знайти швидкість другого тіла; Ш вид – задачі на знаходження часу: дано значення відстані та швидкостей обох тіл, треба визначити час їх спільного руху. Рух в різних напрямках включає два види руху: рух назустріч та рух в протилежних напрямках.
1. Зміст підготовчої роботи до введення задач на одночасний рух. Мета – актуалізувати знання пропорційних величин: відстань, швидкість та час; взаємозв’язків між ними, та спостереження за рухом двох тіл відносно одне одного. Актуалізація знань учнів про пропорційні величини: відстань, швидкість та час здійснюється під час розв’язування простих та складених задач відомих дітям видів. Крім того, на цьому етапі треба повторити не лише взаємозв’язок між даними величинами, а й приділити певну увагу фізичному змісту швидкості. З цією метою учням пропонуються завдання виду: 1. Пояснити зміст речень: - равлик повзе зі швидкістю 6 - літак летить зі швидкістю 950 2. Назвіть швидкість, з якою на вашу думку їде машина: 6 3. Чому дорівнює швидкість руху: - меч-риби, якщо вона за кожну годину пропливає по 100 км; верблюда, якщо він за кожну годину проходить 25 км. 4. Згадайте, як пов’язані між собою величини: відстань, швидкість та час. Складіть за кожним рядком задачу і розв’яжіть ці задачі:
5. Розв’яжіть задачу: Літак за 3 години пролетів 2700 км. Яку відстань він пролетить за 6 годин, якщо летітиме з такою самою швидкістю? (Це задача на знаходження четвертого пропорційного, яка розв’язується двома способами: 1 – способом наведення до одиниці, П – способом відношень). 6. Слон пробігає 360 м за 30 с, а швидкість лева на 28 7. Машина їхала 3 год зі швидкістю 100 Розглянемо останню задачу. Короткий запис складаємо (як звичайно) у формі таблиці:
Крім того до цієї задачі корисно зробити креслення: - Що означає число 100? (Число 100 означає швидкість автомобіля першого разу. 100 - Що означає число 3? (Число 3 означає час руху автомобіля.) - Отже автомобіль за першу годину подолав 100 км (покажемо це відрізком), за другу годину подолав 100 км, за третю годину – 100 км. - Що означає число 120? (Число 120 означає швидкість автомобіля другого разу. 120 - Що означає число 4? (Число 4 означає час руху автомобіля другого разу.) - Отже автомобіль за першу (з 4-х годин) проїхав 120 км (покажемо це відрізком), за другу годину – 120 км, за третю годину – 120 км, за четверту годину – 120 км. - Яке число є шуканим? (Шуканою є загальна відстань, яку подолав автомобіль за весь час руху.) Як це показати на кресленні? (Фігурною дужкою.) 100
Таким чином, діти поступово знайомляться з коротким записом в формі креслення.
На ступені підготовчої роботи також слід узагальнити і систематизувати уявлення дітей про рух назустріч та рух в протилежних напрямах. З цією метою учні спостерігають за рухом одного тіла відносно другого і вчаться схематично зображати рух:
Спостерігаючи за одночасним рухом двох тіл учні роблять висновки про характер зміни відстані між тілами при русі назустріч та при русі в протилежних напрямах, про час руху обох тіл та про величину відстані між тілами на момент початку (закінчення) руху. Спостереження за одночасним рухом назустріч дають підстави зробити такі висновки: 1. Відстань між тілами весь час зменшується. 2. Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3. Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. Спостереження за одночасним рухом в протилежних напрямах дають підстави зробити такі висновки: 1. Відстань між тілами весь час збільшується. 2. Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3. Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. Порівнюючи ці висновки, узагальнюємо їх:
Для глибокого усвідомлення цих висновків учням пропонуються завдання: 1. Із двох міст одночасно назустріч вийшли два пішоходи і зустрілися через 3 години. Скільки часу рухався кожний пішохід? (3 години) 2. З села в місто вийшов пішохід і в цей же час із міста назустріч йому виїхав мотоцикліст, який зустрів пішохода через 40 хвилин. Скільки часу рухався до зустрічі пішохід? (40 хвилин) 3. Два пішохода вийшли одночасно в протилежних напрямах і закінчили свій рух через 2 години. Скільки часу рухався кожний пішохід? Що можна сказати про відстань, яку пройшов кожний пішохід, якщо: - вони рухалися з однаковою швидкістю; (відстань однакова, тому що швидкості однакові в обох пішоходів та час руху, теж однаковий – 2 год.); - швидкість першого більше швидкості другого; (відстань, яку пройшов перший пішохід більша за відстань, яку пройшов другий; при однаковому часі руху, швидкість і відстань змінюються одному напрямі: чим більше швидкість, тим більша відстань). 4. Два лижники вийшли одночасно назустріч один одному. Перший лижник йшов зі швидкістю 12 5. Два велосипедисти виїхали одночасно з одного пункту в протилежних напрямах. Швидкість першого велосипедиста 5 В задачах №4 та №5 слід порівняти отримані числові значення, і зробити висновок:
З метою закріплення зробленого висновку є корисними завдання: 6. Дві черепахи одночасно виринули назустріч одна одній. Швидкість першої черепахи 9 7. Два катера відійшли від пристані одночасно в протилежних напрямах. Швидкість першого катера 25 8. Два лижники вийшли одного селища одночасно в протилежних напрямах. Знайди швидкість другого лижника, якщо відома швидкість першого лижника 5 9. Хлопчик і дівчинка почали одночасно бігти на ковзанах. З якою швидкістю біжить дівчинка, якщо швидкість хлопчика 5 2. Ознайомлення учнів з задачами на одночасний рух на зустріч та одночасний рух в протилежних напрямах: 1) задачі на знаходження відстані і швидкості (1 спосіб) Традиційно учні спочатку знайомляться з трьома видами задач на одночасний рух назустріч, а потім – з задачами на одночасний рух в протилежних напрямах. Між тим, задачі на знаходження відстані при одночасному русі назустріч та в протилежних напрямах мають однакові способи розв’язання. Те ж саме, можна сказати і про задачі на знаходження швидкості та часу. Тому, має сенс розглядати одночасно задачі на рух назустріч та задачі на рух в протилежних напрямах. Треба зазначити, що традиційно учні відразу знайомляться із двома способами розв’язування задач на знаходження відстані і швидкості. Між тим, ці способи принципово відмінні: при розв’язанні першим способом розглядається рух кожного тіла окремо, і лише потім відповідають на запитання задачі; а при розв’язанні другим способом розглядається рух одного тіла відносно другого і дізнаються на скільки змінюється відстань між тілами за одиницю часу – саме це є „ключем” до розв’язання задачі, після чого можна відповісти на її запитання. Практика свідчить, що діти краще засвоюють перший спосіб міркування, другий спосіб викликає у багатьох дітей труднощі. Тому ми пропонуємо спочатку навчити молодших школярів розв’язувати задачі першим способом, а потім – другим; після чого їх порівняти и узагальнити. Таким чином, кожний спосіб є предметом спеціального засвоєння. Задача 1. Два лижника вийшли одночасно назустріч один одному з двох селищ і зустрілися через 3 години. Перший лижник йшов зі швидкістю 12 Розглянемо докладно методику роботи над задачею. - Про що йде мова в задачі? (В задачі йде мова про рух двох лижників. Тому короткий запис задачі буде в формі креслення.) - Що відомо про час початку руху? (Лижники почали рухатися одночасно.) - Як рухаються лижники? (Лижники рухаються назустріч один одному.) Покажемо це на кресленні стрілочками „назустріч”. - Зробіть висновки. 1) Відстань між тілами весь час зменшується. 2) Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3) Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. - Складіть короткий запис задачі. (Над стрілочками записуємо швидкості руху кожного лижника. Поставимо прапорець на місті зустрічі: тут треба подумати, як він розташовується відносно селищ – швидкість першого лижника менше, ніж швидкість другого лижника, на рух вони витратили однаковий час, тобто 3 год; значить перший пройшов меншу відстань, ніж другий. Прапорець треба поставити ближче до першого селища. На рух кожний лижник витратив 3 години, лижники зустрілися через 3 години. Біля прапорця напишемо t = 3 год. Треба знайти відстань між селищами: позначимо її фігурною дужкою. Нагадаємо, що вся відстань складається з відстані, яку пройшов перший лижник та відстані, яку пройшов другий лижник. Покажемо це фігурними дужками.)
t = 3 год 12
? - За коротким записом поясніть числа задачі. (Число 12 позначає швидкість першого лижника. 12 - Яке запитання задачі? Що можна сказати про шукану величину? Як шукана величина пов’язана з іншими величинами? (В задачі запитується про відстань між селищами. Відстань між селищами дорівнює усій відстані, що пробігли разом лижники. Отже, вся відстань складається з відстані, яку пробіг перший лижник та відстані, яку пробіг другий лижник. Щоб знайти відстань, треба швидкість помножити на час.) - Яке запитання задачі? (Яка відстань між селами?) Як ми його пере формулювали? (Яку відстань пройшли обидва лижники разом?) - Що треба знати, щоб відповісти на запитання задачі? (Треба знати два числові значення: 1 – відстань, яку пробіг перший лижник, не відомо, та П – відстань, яку пробіг другий лижник, невідомо.) - Якою арифметичною дією відповімо на запитання задачі? (Дією додавання.) - Чи можна відразу відповісти на запитання задачі? (Не можна, тому що ми не знаємо: 1 – відстану, яку пройшов перший лижник та не знаємо П – відстань, яку пройшов другий лижник.) - Що треба знати, щоб дізнатися про відстань, яку пройшов перший лижник? (Треба знати два числові значення: 1 – швидкість першого лижника, відомо 12 - Якою арифметичною дією відповімо на це запитання? (Дією множення.) - Чи можна тепер відповісти на запитання задачі? (Не можна, тому що ми не знаємо яку відстань подолав другий лижник.) - Що треба знати, щоб про це дізнатися? (Треба знати два числові значення: 1 – швидкість другого лижника, відомо 14 - Якою арифметичною дією відповімо на це запитання? (Дією множення.) - Чи можна тепер відповісти на запитання задачі? (Так, ми від запитання задачі перейшли до числових даних. Аналіз закінчено.)
?
? +?
12 * 3 14 * 3 - Складіть план розв’язування задачі. (Першою дією дізнаємося про відстань, яку пройшов перший лижник. Другою дією дізнаємося про відстань, яку пройшов другий лижник. Третьою дією дізнаємося про відстань, яку пройшли разом обидва лижники і відповімо на запитання задачі.) - Запишіть розв’язання по діях з поясненням. Розв’язання 1) 12 * 3 = 36 (км) – відстань, яку пройшов перший лижник; 2) 14 * 3 = 42 (км) – відстань, яку пройшов другий лижник; 3) 36 + 42 = 78 (км) – відстань, яку пройшли обидва лижники разом; відстань між селищами. Відповідь: 78 км – відстань між селищами.
Робота над задачею після її розв’язання.
- Припустимо, лижники йшли не на зустріч один одному, а одночасно вирушили з одного місця і шли в протилежних напрямах. Запитується: Яка відстань буде між лижниками через 3 години? - Зробіть відповідні зміни у кресленні. t = 3 год 12
? - Що відомо про час початку руху? (Лижники почали рухатися одночасно.) - Як рухаються лижники? (Лижники рухаються в протилежних напрямах.) - Зробіть висновки. 1) Відстань між тілами весь час збільшується. 2) Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3) Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. Далі робота йде аналогічно попередній задачі.
- Складіть план розв’язування задачі. (Першою дією дізнаємося про відстань, яку пройшов перший лижник. Другою дією дізнаємося про відстань, яку пройшов другий лижник. Третьою дією дізнаємося про відстань, яку пройшли разом обидва лижники і відповімо на запитання задачі.) - Запишіть розв’язання по діях з поясненням. Розв’язання 1) 12 * 3 = 36 (км) – відстань, яку пройшов перший лижник; 2) 14 * 3 = 42 (км) – відстань, яку пройшов другий лижник; 3) 36 + 42 = 78 (км) – відстань, яку пройшли обидва лижники разом; відстань між лижниками через 3 год. Відповідь: 78 км – відстань між лижниками через 3 год після початку руху.
- Порівняйте обидві задачі. Що в них спільного? (Діючи особи – лижники. Однакові значення величин: швидкостей та часу. В обох задачах вимагається знайти відстань.) - Чим відрізняються ці задачі? (В першій задачі лижники вирушили одночасно назустріч один одному, а в другий – одночасно в протилежних напрямах.) - Порівняйте розв’язання обох задач. Що цікавого ви помітили? (Обидві задачі мають однакові розв’язання.) Узагальніть план розв’язування таких задач. - Отже, якщо в задачі треба знайти відстань при одночасному русі назустріч або в протилежних напрямах, то її розв’язують за планом:
Задачу на знаходження швидкості вводимо, як обернену задачу до задачі на знаходження відстані.
Задача 3. З двох сіл виїхали одночасно назустріч один одному трактор та бричка з конем. Трактор рухався зі швидкістю 9 7 t = 2 год 9
? Розв’язання 1) 9 * 2 = 18 (км) – відстань, яку подолав трактор; 2) 7 * 2 = 14 (км) – відстань, яку подолала бричка; 3) 18 + 14 = 32 (км) – відстань, яку подолали трактор і бричка разом; відстань між селами. Відповідь: 32 км – відстань між селами.
- Складіть обернену задачу, так, що була невідомою швидкість трактора. (Виписуємо числа задачі і пояснюємо, що означає кожне число: 9, 7, 2, - пряма задача , 7, 2, 32 – перша обернена задача:
Задача 4. З двох сіл виїхали, відстань між якими 32 км, одночасно назустріч один одному вирушили трактор та бричка з конем і зустрілися через 2 години. Чому дорівнює швидкість трактора, якщо швидкість брички 7 Вносимо зміни у короткий запис: t = 2 год ?
32 км
- За коротким записом поясніть числа задачі. (Число 7 позначає швидкість брички. 7 - Яке запитання задачі? Що можна сказати про шукану величину? Як шукана величина пов’язана з іншими величинами? (В задачі запитується про швидкість трактора. Щоб знайти швидкість, треба відстань поділити на час.) - Що треба знати, щоб відповісти на запитання задачі? (Треба знати два числові значення: 1 – відстань, яку проїхав трактор, не відомо, та П – час руху трактору, відомо, 2 год.) - Якою арифметичною дією відповімо на запитання задачі? (Дією ділення.) - Чи можна відразу відповісти на запитання задачі? (Не можна, тому що ми не знаємо: 1 – відстань, яку подолав трактор до зустрічі) - Що треба знати, щоб дізнатися про відстань, яку подолав трактор до зустрічі? (Треба знати два числові значення: 1 – загальну відстань, яку подолали і трактор і бричка, відомо 32 км, та П – відстань, яку подолала бричка, невідомо.) - Якою арифметичною дією відповімо на це запитання? (Дією віднімання.) - Чи можна відразу відповісти на це запитання? (Не можна, тому що ми не знаємо яку відстань подолала бричка.) - Що треба знати, щоб про це дізнатися? (Треба знати два числові значення: 1 – швидкість брички, відомо 7 - Якою арифметичною дією відповімо на це запитання? (Дією множення.) - Чи можна тепер відповісти на запитання задачі? (Так, ми від запитання задачі перейшли до числових даних. Аналіз закінчено.)
?
?: 2
32 -?
7 * 2
- Складіть план розв’язування задачі. (Першою дією дізнаємося про відстань, яку подолала бричка. Другою дією дізнаємося про відстань, яку подолав трактор. Третьою дією дізнаємося про швидкість трактора і відповімо на запитання задачі.) - Запишіть розв’язання по діях з поясненням. Розв’язання 4) 7 * 2 = 14 (км) – відстань, яку подолала бричка; 5) 32 – 14 = 18 (км) – відстань, яку подолав трактор; 6) 18: 2 = 9 ( Відповідь: 9 Робота над задачею після її розв’язання. - Припустимо, трактор і бричка рухалися не на зустріч один одному, а одночасно вирушили з одного селища в протилежних напрямах. Запитується: Яка швидкість брички? - Зробіть відповідні зміни у кресленні. t = 2 год ?
32 км
- Що відомо про час початку руху? (Трактор і бричка почали рухатися одночасно.) - Як вони рухаються? (Трактор і бричка рухаються в протилежних напрямах.) - Зробіть висновки. 1) Відстань між тілами весь час збільшується. 2) Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3) Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. - За коротким записом поясніть числа задачі. (Число 7 позначає швидкість брички. 9 - Яке запитання задачі? Що можна сказати про шукану величину? Як шукана величина пов’язана з іншими величинами? (В задачі запитується про швидкість брички. Щоб знайти швидкість, треба відстань поділити на час.) - Що треба знати, щоб відповісти на запитання задачі? (Треба знати два числові значення: 1 – відстань, яку проїхав бричка, не відомо, та П – час руху брички, відомо, 2 год.) - Якою арифметичною дією відповімо на запитання задачі? (Дією ділення.) - Чи можна відразу відповісти на запитання задачі? (Не можна, тому що ми не знаємо: 1 – відстань, яку подолала бричка до зустрічі) - Що треба знати, щоб дізнатися про відстань, яку подолала бричка до зустрічі? (Треба знати два числові значення: 1 – загальну відстань, яку подолали і трактор і бричка, відомо 32 км, та П – відстань, яку подолав трактор, невідомо.) - Якою арифметичною дією відповімо на це запитання? (Дією віднімання.) - Чи можна відразу відповісти на це запитання? (Не можна, тому що ми не знаємо яку відстань подолав трактор.) - Що треба знати, щоб про це дізнатися? (Треба знати два числові значення: 1 – швидкість трактора, відомо 9 - Якою арифметичною дією відповімо на це запитання? (Дією множення.) - Чи можна тепер відповісти на запитання задачі? (Так, ми від запитання задачі перейшли до числових даних. Аналіз закінчено.)
?
?: 2
32 -?
9 * 2
- Складіть план розв’язування задачі. (Першою дією дізнаємося про відстань, яку подолала бричка. Другою дією дізнаємося про відстань, яку подолав трактор. Третьою дією дізнаємося про швидкість трактора і відповімо на запитання задачі.) - Запишіть розв’язання по діях з поясненням. Розв’язання 1) 9 * 2 = 18 (км) – відстань, яку подолав трактор; 2) 32 – 18 = 14 (км) – відстань, яку подолала бричка; 3) 14: 2 = 7 ( Відповідь: 7
- Порівняйте обидві задачі. Що в них спільного? (Діючи особи – трактор і бричка. Однакові значення величин: швидкості брички, відстані та часу. В обох задачах вимагається знайти швидкість трактора або швидкість брички.) - Чим відрізняються ці задачі? (В першій задачі трактор і бричка вирушили одночасно назустріч один одному, а в другий – одночасно в протилежних напрямах.) - Порівняйте розв’язання обох задач. Що цікавого ви помітили? (Обидві задачі розв’язуються однаковими діями.) Узагальніть план розв’язування задач на знаходження швидкості при одночасному русі в різних напрямках. - Отже, якщо в задачі треба знайти швидкість при одночасному русі назустріч або в протилежних напрямах, то її розв’язують за планом:
Слід порівняти плани розв’язання задач на знаходження відстані і швидкості при одночасному русі назустріч або в протилежних напрямах. І зробити узагальнюючий висновок: Якщо в задачі треба знайти відстань або швидкість при одночасному русі назустріч або в протилежних напрямах, то цю задачу розв’язують за планом:
Можна узагальнити міркування учнів при розв’язуванні задач на знаходження відстані і швидкості при одночасному русі назустріч або в протилежних напрямах: Пам’ятка (1 спосіб: S, V)
1. Про що йде мова в задачі? 2. Що відомо про час початку руху? 3. Як рухаються тіла? 4. Зробіть висновки. 1) Відстань між тілами весь час 2) Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3) Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. 5. Складіть короткий запис задачі. 6. За коротким записом поясніть числа задачі. 7. Складіть план розв’язування задачі.
8. Запишіть розв’язання по діях з поясненням або виразом. 9. Запишіть відповідь до задачі. 10. Складіть і розв’яжіть обернену задачу (на знаходження
2) Задачі на знаходження відстані та швидкості (2 спосіб). Пропонуємо учням розв’язати задачу на знаходження відстані при одночасному русі назустріч відомим способом. Задача 6. З двох селищ одночасно назустріч один одному вирушили хлопчик і дівчинка. Швидкість хлопчика 5 Працюємо над задачею за пам’яткою: 1. Про що йде мова в задачі? (Про рух хлопчика і дівчинки.) 2. Що відомо про час початку руху? (Вони почали рухатися одночасно.) 3. Як рухаються тіла? (Хлопчик і дівчинка рухаються назустріч один одному. Покажемо це стрілочками на кресленні.) 4. Зробіть висновки. 1) Відстань між тілами весь час зменшується. 2) Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло. 3) Кожне тіло на рух витратило однаковий час, тому що вони почали рухатися одночасно і закінчили рухатися одночасно. 5. Складіть короткий запис задачі. tзустр. = 3 год 5
? 6. За коротким записом поясніть числа задачі. (Число 5 означає швидкість хлопчика. 5 2. Складіть план розв’язування задачі. (Першою дією дізнаються про відстань, яку пройшов хлопчик. Другою дією дізнаються про відстань, яку пройшла дівчинка. Третьою дією знайдемо відстань, яку пройшли хлопчик і дівчинка разом, тобто знайдемо відстань між селищами.) 3. Запишіть розв’язання по діях з поясненням. Розв’язання 1) 5 * 3 = 15 (км) відстань, яку подолав хлопчик; 2) 4 * 3 = 12 (км) відстань, яку подолала дівчинка; 3) 15 + 12 = 27 (км) відстань, яку подолали разом хлопчик і дівчинка. 4. Запишіть відповідь до задачі. (Відповідь: 27 км відстань між селищами.)
Робота над задачею після її розв’язання полягає у розв’язанні цієї задачі другим способом. Розглянемо докладно методику навчання учнів розв’язуванню задач на знаходження відстані і швидкості при одночасному русі назустріч або в протилежних напрямах другим способом. Вчитель пропонує учням розв’язати задачу іншим способом. Така пропозиція викликає здивування і активізує пізнавальну активність. Складається проблемна ситуація „ Як розв’язати задачу іншим способом?”. Вчитель викликає хлопчика і дівчинку до дошки і пропонує їм продемонструвати рух дітей. Під час демонстрації руху задаються дітям запитання: - Покажіть на кресленні звідки кожний з вас почав рухатися? - Як ви рухаєтесь? (Назустріч один одному.) Що відбувається з відстанню при одночасному русі назустріч? (Відстань весь час скорочується.) - Яку відстань пройшов кожна дитина до зустрічі? (Хлопчик показує на кресленні відрізок, що відповідає відстані, яку подолав хлопчик. А дівчинка – відрізок, що відповідає відстані, яку пройшла дівчинка.) - Через який час ви зустрілися? (Через 3 години.) - Отже хлопчик (дівчинка) всю цю відстань подолав за 3 години! Тому розділимо кожний відрізок на 3 рівні частини. tзустр. = 3 год 5
?
- Яку відстань пройшов хлопчик за першу годину? (5 км.) Покажіть це на кресленні. - Яку відстань пройшла дівчинка за першу годину? (4 км.) Покажіть це на кресленні. - Відмітимо дужками ці відстані і підпишімо під ними 5 км та 4 км. tзустр. = 3 год 5
5 км 4 км
? - На скільки кілометрів наблизилися діти за першу годину? (На 5 + 4 = 9 км.) - Пройшла друга година. Скільки кілометрів за цю годину пройшов хлопчик? Дівчинка? На скільки кілометрів вони наблизилися за другу годину? (На 5 + 4 = 9 км.) Покажемо це на кресленні. - Пройшла тертя година. Скільки кілометрів за цю годину пройшов хлопчик? Дівчинка? На скільки кілометрів вони наблизилися за третю годину? (На 5 + 4 = 9 км.) Покажемо це на кресленні. tзустр. = 3 год 5
5 км 5 км 5 км 4 км 4км 4 км
? - На скільки кілометрів наближалися діти за кожну годину? (На 5 + 4 = 9 км.) - За 3 години діти зустрілися. Скільки „разів” вони наближалися на 9 км? (3 рази.) На скільки кілометрів вони наблизяться за 3 години? (9 * 3 = 27 км) - Як по іншому розв’язати задачу? Розкажіть план розв’язування задачі. (Першою дією дізнаємося на скільки кілометрів наближаються діти за кожну годину. Другою дією дізнаємося на скільки кілометрів наблизяться діти за 3 години, тобто дізнаємося про відстань, яку подолали діти разом – відстань між селами.) - Запишіть розв’язання по діях з поясненням. Розв’язання 1) 5 + 4 = 9 (км) на стільки наближаються діти одне до одного за кожну годину; 2) 9 * 3 = 27 (км) на стільки наблизяться діти одне до одного за 3 години. Відповідь: 27 км – відстань між селищами.
Далі учням пропонується перетворити цю задачу в задачу на одночасний рух в протилежних напрямах і розв’язати її двома способами. Задача 7. З одного селища одночасно в |
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1948; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.3.204 (0.012 с.) |

 ;
; .
. .
. більша за швидкість слона. Яку відстань пробіжіть лев за 9 с? (Це ускладнена задача на знаходження четвертого пропорційного – задача, пов’язана з одиничною нормою.)
більша за швидкість слона. Яку відстань пробіжіть лев за 9 с? (Це ускладнена задача на знаходження четвертого пропорційного – задача, пов’язана з одиничною нормою.) :
1. Відстань між тілами весь час
:
1. Відстань між тілами весь час  .
2. Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло.
.
2. Весь шлях складається зі шляху, який подолано першим тілом та шляху, який подолало друге тіло.
 , а швидкість другої черепахи 5
, а швидкість другої черепахи 5  . Як змінюється відстань між черепахами? На скільки дм зменшується відстань між черепахами за кожну секунду?
. Як змінюється відстань між черепахами? На скільки дм зменшується відстань між черепахами за кожну секунду?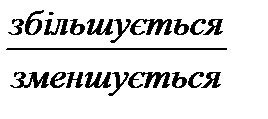 .
.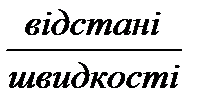 ) або перетворіть задачу у задачу на
) або перетворіть задачу у задачу на  .
.


