
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі на рух в одному напрямкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Підготовча робота. На ступені підготовчої роботи учні повинні: 1) спостерігати за рухом двох тіл наздогін; 2) усвідомити, що коли швидкість тіла, що рухається позаду 3) зробити висновок: знайти на скільки Після спостереження учнями руху в одному напрямі (у випадках, коли швидкість тіла, що наздоганяє більше або менше швидкості тіла, що рухається попереду), учні роблять висновок:
Далі треба з’ясувати, як дізнатися на скільки змінюється відстань між тілами за одиницю часу. Для цього розглядається ситуації: 1. Хлопчики змагаються у бігу. Вони одночасно стартували. При чому швидкість першого хлопчика 8 Пояснюємо числа задачі. (Число 8 означає швидкість першого хлопчика, 8 Робимо креслення: 8 6
За 1 секунду перший хлопчик пробігає 8 м, а другий – 6 м; 8 більше 6, тому другий хлопчик буде відставати від першого. Щоб дізнатися на скільки він буде відставати, треба з більшого числа відняти менше: 8 м
? П
6 м
З метою закріплення зробленого висновку корисні завдання: 1) Перша черепаха рухається за другою черепахою. Швидкість першої 8 8
Розв’язання Відстань між черепахами за кожну хвилину скорочується, тому що швидкість тієї черепахи, що рухається позаду більша за швидкість черепахи, що рухається попереду. Перша черепаха за кожну хвилину долає 8 дм, а друга – 6 дм. У той час, коли перша черепаха наблизилася до другої на 8 дм, друга від неї віддалилася на 6 дм. Але 8 дм більше за 6 дм., тому все ж таки відстань між черепахами скорочується на: 8 – 6 = 2 (дм) Відповідь: відстань між черепахами скорочується на 2 дм за кожну хвилину.
2) Вітер зірвав з голови чоловіка капелюх. Побачивши це, чоловік побіг за своїм капелюхом. Чи дожене чоловік власний капелюх, якщо вітер несе капелюх зі швидкістю 7 6
Розв’язання Відстань між чоловіком і його капелюхом за кожну секунду збільшується, тому що швидкість чоловіка, а він рухається позаду менша за швидкість капелюха, який несе вітер. Чоловік за кожну хвилину долає 6 м, а „капелюх” – 7 м. У той час, коли чоловік наблизилася до капелюха на 6 м, капелюх від нього віддалилася на 7 м. Але 6 м менше за 7 м., тому відстань між чоловіком і капелюхом збільшується на: 7 – 6 = 1 (м) Відповідь: відстань між чоловіком і капелюхом збільшується на 1 м за кожну хвилину.
З метою подолання вузького узагальнення, слід пропонувати аналогічні завдання й на рух назустріч і в протилежних напрямах:
4) Танцюристи на ковзанах при виконуванні парної ластівки з різних боків льодового стадіону почали рухатися одночасно назустріч один одному. Хлопчик рухається зі швидкістю 8
5) Мисливець зустрів у лісі ведмедя. Обидва злякалися і побігли у протилежних напрямах. Як змінюється відстань між ними за кожну секунду і на скільки, якщо ведмідь біжить зі швидкістю 3 Після розв’язання аналогічних завдань учні дістають висновків: 1. Відстань при одночасному русі назустріч скорочується на суму відстаней, яку проходить кожне тіло за одиницю часу. 2. Відстань при одночасному русі наздогін скорочується на різницю відстаней, яку проходить кожне тіло за одиницю часу. Потім можна переходити до ознайомлення учнів с задачами на рух наздогін, при чому це доцільно робити у порівнянні руху назустріч та руху наздогін. Розглянемо це питанням докладно.
Ознайомлення с задачами на рух наздогін. Задача 1. Відстань між двома лижниками на момент початку руху складала 44 м. Вони почали рухатися одночасно
t -? t -? 12
44 м 44 м
Задача 2. Відстань між двома чоловіками на момент початку руху була 600 м. Вони одночасно почали рухатися
t – 2 хв. t – 2 хв. 170
600 м 600 м
З метою закріплення учням пропонуються задачі на знаходження відстані у співставленні задач на рух наздогін та рух з відставанням: Задача 3. Два велосипедиста знаходяться на відстані 240 м один від одного. Швидкість першого велосипедиста 5 1) перший їде за другим; 2) другий їде за першим?
t = 30 с t = 30 с 5
240 м 240 м
- Поясніть числа задачі: 5, 3, 240, 30, 5, 3, 240, 30, - Складіть і розв’яжіть обернені задачі на знаходження відстані, яка була на момент початку руху. 5, 3, 240, 30, 180 5, 3, 240, 30, 300
Задача 4. Два велосипедиста почали рухатися одночасно в одному напрямі. Швидкість першого велосипедиста 5 1) 180 м, при чому перший їде за другим; 3) 300 м, при чому другий їде за першим? t = 30 с t = 30 с 5
??
- Складіть і розв’яжіть обернені задачі на знаходження швидкості. 5, 3, 240, 30, 180 5, 3, 240, 30, 300
Задача 5. Два велосипедиста знаходяться на відстані 240 м один від одного. Яка швидкість першого велосипедиста, якщо швидкість другого велосипедиста 3 1) перший їде за другим та через 30 с після початку руху відстань між ними складала 180 м; 2) другий їде за першим та через 30 с після початку руху відстань між ними складала 300 м
t = 30 с t = 30 с ? 3
240 м 240 м
- Складіть і розв’яжіть обернені задачі на знаходження часу.
5, 3, 240, 30, 300
Задача 6. Два велосипедиста знаходяться на відстані 240 м один від одного. Швидкість першого велосипедиста 5 1) 180 м, якщо перший їде за другим; 2) 300 м, якщо другий їде за першим.
t -? t -? 5
240 м 240 м
Наведемо приклад роботи над задачею на рух в одному напрямі. Задача 7. Колобок котиться бабуся Шапокляк гониться за Чебурашкою. Зараз між ними відстань 1100 м. Швидкість Шапокляк 120 - Про що йде мова в задачі? (Про рух Шапокляк та Чебурашки.) - Що відомо про час початку руху? (Вони вирушили одночасно.) - Як вони рухаються? (Шапокляк біжить за Чебурашкою. Вони рухаються в одному напрямі.) - Які висновки можна зробити при русі в одному напрямі?(Швидкість Шапокляк більша за швидкість Чебурашки, тому відстань між ними буде весь час зменшуватися. На рух вони витратять однаковий час.) - Зробимо креслення. t -? 120
1100 м - За коротким записом поясніть числа задачі. (Число 120 означає швидкість Шапокляк. 120 - Що треба знати, щоб відповісти на запитання задачі? (Треба знати два числові значення: 1 – відстань, яка була між ними на момент початку руху, відомо 1100 м, та П – відстань, на яку зменшується відстань між Шапокляк та Чебурашкою за кожну хвилину, невідомо.) - Якою арифметичною дією відповімо на запитання задачі? (Дією ділення.) - Чи можна відразу відповісти на запитання задачі? (Ні, ми не знаємо відстань, на яку зменшується відстань між Шапокляк та Чебурашкою за кожну хвилину.) - Що треба знати, щоб про це дізнатися? (Треба знати два числові значення: 1 – на скільки наближається за кожну хвилину Шапокляк до Чебурашки, відомо на 120 м, та П – на скільки віддаляється Чебурашка від Шапокляк за кожну хвилину, відомо, на 100 м.) - Якою арифметичною дією відповімо на це запитання? (Дією додавання.) - Чи можна відразу відповісти на це запитання. (Так, ми від запитання перейшли до числових даних. Аналіз закінчено.)
?
1100:?
120 - 100
- Складіть план розв’язування задачі. (Першою дією дізнаємося відстань, на яку зменшується відстань між Шапокляк та Чебурашкою за кожну хвилину. Другою дією дізнаємося через скільки хвилин Шапокляк дожене Чебурашку.) - Запишіть розв’язання задачі виразом. Розв’язання 1100: (120 – 100) = 55 (хв..) Відповідь: через 55 хвилин Шапокляк дожене Чебурашку.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1726; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.77.244 (0.007 с.) |

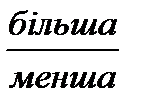 за швидкість тіла, що рухається попереду, то відбувається
за швидкість тіла, що рухається попереду, то відбувається 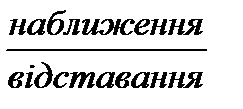 одного тіла
одного тіла  другого.
другого. відстань між тілами за одиницю часу, треба відніманням.
відстань між тілами за одиницю часу, треба відніманням. .
Перше тіло
.
Перше тіло  друг
друг  тіл
тіл 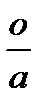 .
.
 , а швидкість другого 5
, а швидкість другого 5  , швидкість другої – 6
, швидкість другої – 6 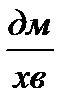 . Як змінюється відстань між черепахами? На скільки змінюється відстань між черепахами за кожну хвилину?
. Як змінюється відстань між черепахами? На скільки змінюється відстань між черепахами за кожну хвилину?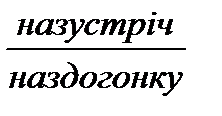 один одному. Швидкість першого лижника 12
один одному. Швидкість першого лижника 12  а швидкість другого 10
а швидкість другого 10 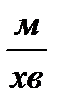 10
10 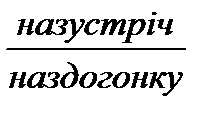 один одному і опинилися разом через 2 хвилини. Яка швидкість другого чоловіка, якщо швидкість першого 170
один одному і опинилися разом через 2 хвилини. Яка швидкість другого чоловіка, якщо швидкість першого 170  , а швидкість Чебурашки 100
, а швидкість Чебурашки 100 


