
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема:многокутник та його периметр. Рівні фігуриСодержание книги
Поиск на нашем сайте
Клас. Математика Тема:Многокутник та його периметр. Рівні фігури Мета: навчальна: сформувати поняття многокутника, периметра многокутника, рівних фігур; сформувати вміння розпізнавати та будувати многокутники, обчислювати периметр многокутника; розвивальна: формувати вміння застосовувати свої знання і власний досвід у нових ситуаціях; виховна: виховувати свідоме ставлення до навчання. Тип уроку: засвоєння нових знань і вмінь. Обладнання: зошити, підручники, лінійки, макети рівних фігур, моделі многокутників. Література: Математика: підруч. для 5 класу загальноосвіт. навч. закл. / Бевз Г.П., Бевз В. Г. – К.: Зодіак - ЕКО, 2005. – 352с. Хід уроку І. Організаційний момент Вчитель перевіряє готовність учнів до уроку, налаштовує їх на роботу. ІІ. Перевірка домашнього завдання Вчитель перевіряє чи виконали учні домашнє завдання, якщо учні щось не зрозуміли, пояснює. ІІІ. Актуалізація опорних знань 1. Усне фронтальне опитування 1) Що називають ламаною? 2) Що таке ланка ламаної? вершина ламаної? 3) Яку ламану називають замкненою? 4)Що називають периметром фігури? 5)Чи може периметр перевищувати суму будь-яких двох сторін фігури? 6)Чи може периметр фігури бути меншим за суму будь-яких двох її сторін? 2. Виконання графічних вправ 1) Побудуйте незамкнену ламану, яка складається: а) з чотирьох ланок, жодні з яких не перетинаються; б) з шести ланок, дві з яких перетинаються. 2) Побудуйте замкнену ламану, яка складається: а) з п'яти ланок, жодні з яких не перетинаються; б) з чотирьох ланок, дві з яких перетинаються. 3. Вкажіть серед наведених відрізків рівні, якщо: AB = 5 см 3 мм, CD = 4 м 5 см, PK = 45 см, EF = 2 дм 8 мм, TQ = 53 мм, MN = 208 мм. V. Закріплення вивченого матеріалу. Усно: №304. Письмово: №306,316, 323, 337. VІ. Підсумки уроку. Пояснення домашнього завдання. Виконання практичної роботи Учитель роздає учням паперові моделі різних за видом многокутників. Завдання: 1) Серед наявних фігур виберіть п'ятикутник [шестикутник]. 2) Побудуйте в зошиті фігуру, що дорівнює обраній вами. 3) Позначте побудований многокутник. 4) Виміряйте його сторони і кути. Зробіть відповідні записи. 5) Знайдіть периметр многокутника. Чому дорівнює сума його кутів? VII. Домашнє завдання Опрацювати § 16, виконати №757, №767, №778, №780. Клас. Математика Тема: Цілі числа. Раціональні числа Мета: навчальна: сформувати поняття цілих та раціональних чисел, навчити розпізнавати цілі, дробові, цілі додатні, цілі від’ємні, раціональні числа; розвивальна: розвивати позитивні риси особистості, логічне мислення, кмітливість, культуру математичного мовлення, пам’ять; виховна: самостійність, впевненість у собі. Тип уроку: узагальнення і систематизація знань. Обладнання: підручники, зошити, дидактичний матеріал (картки із завданнями). Література: Мерзляк А.Г., Полонський В.Б., Якір М.С./ Математика: підруч. для 6 кл. загальноосвіт. навч. закл. – Х.: Гімназія, 2006. – 304с. Хід уроку І. Організаційний момент Вчитель вітається з учнями, перевіряє їх присутність. ІІ. Перевірка домашнього завдання Вчитель перевіряє чи виконали учні домашнє завдання. РАЦІОНАЛЬНІ ЧИСЛА
Є ще інші види дій з числами, а тому існують й інші види чисел. V. Відпрацювання навичок Усні вправи: №878, 879. Письмові вправи: №881, 883(1,2), 885, 887(1,3,5), 892. V I. Домашнє завдання §4, п.30, №877, 880, 882, 883(3,4), 888.
Клас. Алгебра І. Організаційний момент Вчитель перевіряє готовність учнів до уроку. Налаштовує їх на роботу. ІІ. Перевірка домашнього завдання Для урізноманітнення роботи з навчальним матеріалом перевірку домашнього завдання можна провести у формі гри «Знайди помилку». Виконання усних вправ 1. Розв’яжіть рівняння:
Що означає «розв’язати рівняння»? 2. Складіть рівняння за умовою задачі: 1) довжина прямокутника 2) ширина прямокутника 3) ширина прямокутника Якщо можна, розв’яжіть рівняння, знайдіть довжини сторін прямокутника. 3. Чи належить графіку функції 4. Чи є дана рівність правильною:
VII. Підсумки уроку Контрольні запитання 1. Що називається розв’язком рівняння з двома змінними? Чи є пара (2; 1) розв’язком рівнянь:
2. Які рівняння з двома змінними називають рівносильними? Наведіть приклад. 3. Що таке графік рівняння з двома змінними? VIII. Домашнє завдання §24.№ 977,979, 984(а,г), 985(б), 991, 995.
Клас. Геометрія Хід уроку. Випереджувальне домашнє завдання: Група істориків – готувала історичні відомості про трикутник Група дослідників – готувала презентацію «Трикутник у побуті» Всі учні – готували макети заготовки трикутників І. Організаційний момент: Вчитель вітається з учнями. ІІ. Мотивація У нас буде незвичайний урок, ми з вами будемо мандрувати по галактиці Геометрія на ракеті Оріон (Слайд1-3). Виступає група Істориків IV. Формулювання теми уроку Запишіть у своїх зошитах тему сьогоднішнього уроку (слайд 16). Дома ви зробили макети - заготовки трикутників. Зараз попрацюємо з ними. Які є види трикутників. Сформулюйте їх визначення (слайд 17-20). Група Істориків Евклід говорив: «Катети – це сторони, що укладають прямий кут». У Древній Греції вже був відомий спосіб побудови прямокутного трикутника на місцевості. Для цього використовували мотузок, на якому були зав'язані 12 вузликів, на однаковій відстані один від одного (слайд 21-26). Ми наближаємося до планети Трикутники у нас залишилося невідомим лише одне питання. Де використовуються трикутники у сучасному житті (слайд 27). Дома група дослідників готувала презентацію по даному питанню. Надамо їм слово. VI. Закріплення знань Робота з підручником Виконати: № 386, №407 VІІ. Підсумок Отже подорож завершилася. Всі молодці, гарно попрацювали. VІІІ. Домашнє завдання. Опрацювати п.13 Виконати №387 №406 *Скласти кросворд, із ключовим словом Трикутник
Клас. Алгебра ХІД УРОКУ Епіграф до уроку: Чим більше я знаю, тим більше вмію. І. Організаційний етап Вчитель вітається з учнями перевіряє їх готовність. Виконання письмових вправ 1) На дошці «вітаміни» з прикладами. Ваше завдання: спростити вираз і дізнатися, які вітаміни найбільше необхідні в щоденному раціоні людини:
Довідка про вітаміни Вітамін А: необхідний для нормального росту й розвитку стану шкіри й імунітету; дефіцит цього вітаміну приводить до курячої сліпоти, ризику появи злоякісних пухлин. Вітамін С: відповідає за імунітет, цілісність стінок судин. Вітамін Д: дефіцит вітаміну веде до зниження міцності кісткової тканини. Вітамін Е: необхідний для нормального статевого розвитку дівчат та хлопців. Вітамін В6: підтримує нормальний стан слизистих та шкіри. 2) Подайте вираз у вигляді степеня й дізнайтеся, в яких продуктах міститься найбільша кількість вітамінів:
3) Знайдіть значення виразу:
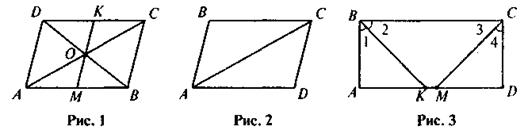
VI. Підбиття підсумків, оцінювання результатів уроку Рефлексія 1) Що нового ви дізналися сьогодні на уроці? 2) Що сподобалося під час уроку? Клас. Геометрія Хід уроку I. Організаційний етап Вчитель вітається з учнями, перевіряє їх присутність. II. Перевірка домашнього завдання Правильність виконання письмових завдань домашньої роботи вчитель перевіряє, зібравши зошити учнів на перевірку. III. Формулювання мети і завдань уроку Учитель нагадує учням про стратегічну мету вивчення розділу, яка була намічена раніше: узагальнити відомості про многокутники та геометричні величини, пов'язані з поняттям многокутника. Узагальнити відомості, які здобули учні в початкових класах та з життєвого досвіду, про зміст та властивості поняття «площа», а також довести справедливість відомої з початкових класів формули площі прямокутника — не і є головна мета уроку. VI. Актуалізація опорних знань Для успішного засвоєння учнями змісту понять уроку та можливості вільно їх використовувати під час розв'язування змістових задач учням слід активізувати знання і вміння щодо одиниць вимірювання площ; ознак рівності трикутників; властивостей паралелограмів; означення і властивостей прямокутника і квадрата та формул периметрів цих чотирикутників. Виконання усних вправ 1. На підлозі розстелені два килими: один площею 6 м2, другий — 8 м2. Килими частково накладені один на одного — по фігурі, площа якої дорівнює 1 м2. Яку площу підлоги закривають килими? 2. Під час вимірювання площ земельних ділянок використовують різні одиниці вимірювання. Що означає гектар; ар? 3. Що означає «сотка» городу? 4. Чи одне й те саме означають ар і сотка? 5. ABCD — паралелограм (рис. 1). Доведіть, що ОМ = ОК.
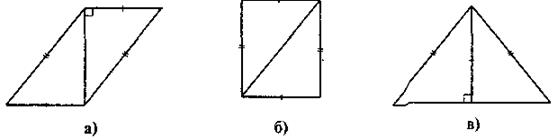
6. ABCD — паралелограм (рис. 2). Доведіть, що Δ ABC = Δ CDA. 7. ABCD — прямокутник, ВК = СМ. 8. Чи правильні твердження? 1) Кожний квадрат є прямокутником. 2) Існує ромб, який є прямокутником. 3) Жодний прямокутник не є ромбом. 4) Існує квадрат, який не є ромбом. V. Засвоєння знань План вивчення нового матеріалу 1. Зміст поняття «площа многокутника». 2. Одиниці вимірювання площ. 3. Спосіб наближеного обчислення площ. 4. Аксіоми площ. 5. Рівновеликі фігури. Рівноскладені многокутники. Властивість рів-носкладених многокутників. 6. Теорема про площу прямокутника. Площа квадрата. Для того щоб правильно розставити акценти, під час викладення матеріалу вчителю слід дотримуватися змісту підручника.
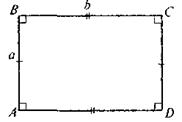
З метою закріплення термінології (рівновеликі фігури, рівноскладені многокутники, властивість рівновеликих многокутників) та формул площ прямокутника і квадрата учні мають розв'язати усні вправи. Виконання усних вправ 1. Площі двох многокутників рівні. Чи означає це, що самі многокутники також рівні? 2. Два прямокутники мають рівні периметри. Чи є вони рівновеликими? 3. Через середини двох протилежних сторін паралелограма проведено пряму. В якому відношенні вона ділить площу паралелограма? 4. Визначте, які з наведених тверджень правильні: а) якщо діагоналі двох квадратів рівні, то ці квадрати рівновеликі; б) два рівновеликі прямокутники рівні; в) два рівновеликі квадрати рівні. 5. Сторона квадрата дорівнює меншій стороні прямокутника. Яка з цих фігур має більшу площу? 6. У трикутнику ABC проведено середні лінії. Вони поділили трикутник на 4 частини. Площа однієї з частин дорівнює 10. Чому дорівнюють площі інших частин? 7. Як розрізати на частини два рівних маленьких квадрати, щоб із цих частин можна було скласти один великий квадрат? 8. Визначте площу квадрата, описаного навколо кола, радіус якого R. 9. Квадрат і прямокутник мають рівні площі. Сторона квадрата дорівнює 12, а одна зі сторін прямокутника — 9. Чому дорівнює друга сторона прямокутника? 10. Периметр квадрата дорівнює 32. Чому дорівнює площа цього квадрата? Виконання письмових вправ 1. Знайдіть площу прямокутника ABCD, якщо. а) АВ = 9см, ВС = 4см; б) АВ: ВС = 5: 1, PABCD = 48см; в) AD = 12см, АС = 13см. 2. Діагональ квадрата дорівнює 12 3. Площа прямокутника дорівнює 128 см2. Знайдіть сторони прямокутника, якщо одна з них удвічі більша за іншу. 4. Бісектриса кута прямокутника ділить його сторону на відрізки завдовжки 3 см і 4 см. Знайдіть площу прямокутника. Скільки розв'язків має задача? VII. Підсумки уроку Для фігур, зображених нарис. 4, доберіть відповідне поняття: рівні, рівновеликі, рівноскладені. Поясніть свій вибір. a) ABCD — прямокутник б) MNKP — квадрат
VIII. Домашнє завдання Вивчити зміст понять, що розглядалися на уроці. Розв'язати задачі. 1. Сторони прямокутника дорівнюють 9 см і 25 см. Знайдіть периметр квадрата, рівновеликого даному прямокутнику. Площа квадрата дорівнює 32 см2. Знайдіть його.
Клас. Алгебра Хід уроку I. Організаційний етап Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу. II. Перевірка домашнього завдання Перевірку виконання письмових вправ можна, провести у формі само- або взаємоперевірки за зразком. Тестові завдання 1. Функція y = f(x) зростаюча, якщо: а) х 2 > х 1; б) у 2 > у 1; в) при х 2 > х 1 f(x 2 ) < f(x1); г) при х 2 > х 1 f(x 2 ) > f(x 1 ). 2. Функція y = f(x) спадна, якщо: а) х 2 < х 1; б) f(x 2 ) < f(x l ); в) при х 2 < х 1 f(x 2 ) < f(x l ); г) при х 2 > х 1 f(x 2 ) < f(x 1 ). 3. Якщо відомо, що f (3) = 0, то: а) х = 3 є нулем функції у = f(x); б) у = 3 є нулем функції y = f(x); в) х = 0 — це нуль функції у = f(x); г) функція y = f(x) має нулі. V. Закріплення знань Усні вправи 1. Розв'яжіть рівняння: 1) х 2 – 3 х + 2 = 0; 2) 3 x – 1 = 0; 3) kx + b = 0 k 2. Розв'яжіть нерівність: 1) 5 – х ≥ 0; 2) 1 – 3 x < 0; 3) 2 х – 3 > 2 x – 5; 4) - х + 3 < - х – 1. 3. У яких проміжках f(x) < 0, якщо: 1) f(x) = 1 – 2 x; 2) f(x) = 4 x – 2? 4. Відомо, що х 1, х 2, х 3 — нулі функції f(x), причому f(x) > 0 на проміжках (х 1, х 2) і (х 3; +∞); і f(x) < 0, якщо х
Методичний коментар Під час розв'язування учнями усних вправ слід вимагати від них аргументованих відповідей (тобто пояснень із посиланням на відповідне означення, а також точного відтворення цього означення). VІ. Закріплення знань Письмові вправи 1) знайти нулі, проміжки знакосталості, проміжки зростання та проміжки спадання деякої функції, заданої графічно; 2) за допомогою обчислень знайти нулі функції, заданої формулою y = f(x); 3) за допомогою обчислень визначити, зростає чи спадає дана функція на заданому проміжку. Проте до названих вправ додаємо вправи на дослідження елементарних функцій (лінійної, оберненої пропорційності, квадратичної функції та функції у = До названих вправ бажано додати вправи на повторення матеріалу попередніх уроків — на відшукання області визначення функції, заданої формулою y = f(x), і на відпрацювання навичок роботи з поняттям графіка функції та оперативних умінь роботи з формулою y = f(x). VIІ. Підсумки уроку Контрольні запитання 1. Яка з даних функцій є спадною (спадає на кожному проміжку своєї області визначення)? 1) у = 2; 2) у = 2. Яка з даних функцій додатна на проміжку (2; +∞)? VIІI. Домашнє завдання 1. Вивчити зміст означень, розглянутих на попередньому уроці, та виділені на цьому уроці властивості елементарних функцій. 2. Розв'язати вправи на застосування вивчених означень та фактів. 3. Повторити зміст поняття «графік функції».
Клас. Геометрія Хід уроку Фронтальна бесіда 1) Дайте означення симетрії відносно точки. 2) Які фігури називаються центрально-симетричними? Наведіть приклади. 3) Укажіть координати точки, яка симетрична точці A (a; b)відносно початку координат. Виконання вправ 1. Побудуйте довільний трикутник ABC і симетричний йому трикутник відносно осі: а) АВ; б) ВС. 2. Скільки осей симетрії має: а) коло; б) прямокутник; в) квадрат; г) ромб; д) рівносторонній трикутник?
Розв'язування задач 1. Побудуйте довільний трикутник і трикутник, симетричний даному, відносно прямої, якщо вона: а) розміщена поза трикутником; б) має лише одну спільну точку з трикутником; в) перетинає дві сторони трикутника. 2. Чотирикутник ABCD заданий координатами своїх вершин: А (1; 1); В (-3; 2), С (-1; -2), D (5; -3). Знайдіть координати вершин чотирикутника, який симетричний даному відносно осі: а) Ох; б) Оу. 3. Доведіть властивості симетрії відносно прямої. 4. Запишіть рівняння кола, яке симетричне колу (х – 1)2 +(у + 2)2 = 1 відносно: а) осі Ох; б) осі Оу. 5. Запишіть рівняння прямої, яка симетрична прямій х + у = 1 відносно: а) осі Ох; б) осі Оу. 6. Дано пряму MN і точки А і В в різних півплощинах відносно MN і на різній відстані від неї. Через точки А і В проведіть прямі так, щоб кут між ними ділився прямою MN навпіл.
V. Домашнє завдання 1. Вивчити теоретичний матеріал. 2. Розв'язати задачі. 1) Запишіть рівняння кола, яке симетричне колу (х + 1)2 + (у + 1)2= 1 відносно: а) осі Ох; б) осі Оу. 2) Запишіть рівняння прямої, яка симетрична прямій х – у = 1 відносно: а) осі Ох; б) осі Оу.
Клас. Алгебра Рівень стандарту Графічний диктант». Учні в зошитах відповідають на питання, «так», «ні». 1. Функція виду у = кх + в називається квадратичною. (Ні). 2. Область визначення функції – це множина тих значень, яких може набувати аргумент. (Так). 3. Функцію можна задати лише аналітичним і графічним способом. (Ні). 4. Функцією називається залежність змінної у від змінної х, якщо кожному значенню х відповідає єдине значення у. (Так). 5. Функція називається парною, якщо f(-x) = -f(x) (Так). 6. Функція у = є спадаючою. (Ні). 7. Функція буде зростаючою на проміжку, якщо більшому значенню аргумента відповідає більше значення функції. (Так). 8. Нулями функції називаються значення аргумента, при яких функція дорівнює нулю. (Так). 9. Графіком функції у=х2 є гіпербола (Ні). 10. Графіком лінійної функції є пряма. (Так). 11. Функція у=х2 проходить через початок координат. (Так). 12. Область визначення функції у = – є множина дійсних чисел. (Ні). (Після виконання учні обмінюються зошитами і перевіряють роботи один одного, правильні відповіді проектуються на екран. Кожна правильна відповідь – 1 бал). «Експерти» заносять оцінки до бланків оцінювання. Робота в мікрогрупах. Завдання №1: презентувати функції. 1) у= кх +в; 2) у=к/х; 3) у= х2; «Експерти»оцінюють роботу членів мікрогруп і фіксують її результати в бланках оцінювання. Завдання №2: 1) для«художників». Варіант І. Накреслити ескіз графіка функції f(х), використовуючи такі відомості про функцію: - Нулі функції х = -6, х = 0, х = 6. - Найменше значення функції – 2 досягається, коли х = - 3; якщо х = 3 то у = 2. - Функція спадає на проміжках [-8; -3] і [3; 8]. - Функція зростає на проміжку [-3; 3]. Варіант ІІ. Накреслити ескіз графіка функції f(х), використовуючи такі відомості про функцію: - Нулі функції х = -6, х = 0, х = 6. - Найменше значення функції – 2 досягається, коли х = -3; якщо х = 3 то у = 2. - Функція спадає на проміжках [-8; -3] і [3; 8]. - Функція зростає на проміжку [-3; 3]. 2) для«аналітиків». За графіком функції, поданим на малюнку, описати властивості функцій. Презентація результатів роботи мікрогруп. Обговорення презентацій. Оцінка роботи членів мікрогруп «Експертами», та викладачем. IV. Повідомлення домашнього завдання. Завдання: Накреслити ескіз графіка функції f(х), використовуючи такі відомості про функцію: - Нулі функції х = -2, х = 0, х = 6. - Найменше значення функції -5 досягається, коли х =2; якщо х = 6 то у = 4. - Функція спадає на проміжках [-7; -2] і [....]. - Функція зростає на проміжку [.....]. За графіком функції, поданим на рисунку, описати її властивості. V. Підбиття підсумків уроку. Виставлення та коментування оцінок. Рефлексія. Завдання: продовжити речення «Сьогодні на уроці відкриттям для мене стало…». Рівень академічний Хід уроку І. Організаційний момент Перевірка готовності учнів до уроку, налаштування на роботу. Лінійна функція 1. Дано функцію у=kx+b. а) Укажіть область визначення та множину значень цієї функції; б) визначте, зростає чи спадає ця функція, якщо k>0, k<0, k=0; в) доведіть, що графіком функції є пряма, визначте геометричний зміст коефіцієнтів k і b; г) опишіть положення прямої відносно осей координат у випадках, якщо: b=0; k=0; k=b=0; д) запишіть рівняння осі ординат. 2. Запишіть рівняння прямої, що: а) має кутовий коефіцієнт k =3 і проходить через точку з координатами (-2;5); б) відсікає від осі ординат відрізок b =-2 і проходить через точку з координатами (-1;8); в) проходить через точки з координатами (-3;2) і (2;-1). 3. Які з функцій 2х+у=0, х-2у=0, 2х+3у=6, 5х-3у+15=0 є зростаючими? Спадними? Квадратична функція 1. Дано функцію у = а)при будь-яких значеннях аргумента функція набуває невід’ємних значень; б) на проміжку (-∞;0) функція спадає: на проміжку (0: +∞) функція зростає; в) при х=0 функція набуває найменшого значення, що дорівнює 0: г) побудуйте графік функції. 2. Дано функцію а) подайте цю функцію у вигляді б) визначте координати в) визначте чи перетинає парабола вісь О г) побудуйте схематично графік цієї функції та за графіком укажіть проміжки знакосталості, проміжки зростання і спадання функції. Дробово-лінійна функція 1. Дано функцію а) знайдіть область визначення та множину значень цієї функції; б) визначте, при яких значеннях аргумента функція набуває додатних.ю відє’мних значень. Розгляньте випадки, якщо в)укажіть проміжки зростання і спадання функції. 2. Побудуйте графік функції, якщо: а) Яку назву має фігура, що є графіком цієї функції? 3. Як змінюється розташування віток гіперболи відносно осей координат: а) залежна від знака коефіцієнта б) під час зміни абсолютної величини коефіцієнта Функція 1. Знайдіть область визначення та множину значень цієї функції. 2. Доведіть, що функція 3. Доведіть, що функція 4. Доведіть, що функція 5. Побудуйте графік функції а) б) Яку назву має фігура, що є графіком цієї функції? Функція 1. Знайдіть область визначення та множину значень цієї функції. 2. Доведіть, що дана функція зростає на всій області визначення. 3. Чи може бути функція бути парною або непарною? 4. у яких координатних чвертях розташований графік цієї функції? V. Підбиття підсумків уроку Заповніть порожні місця в таблиці «Основні види функцій, їх властивості та графіки».
VІ. Домашнє завдання Повторити зміст понять, що були розглянуті на уроці. Опрацювати §2, п.3, вправи 50, 57, 66, 78.
Профільний рівень Хід уроку І. Організаційний етап Вчитель вітається з учнями, перевіряє їх присутність. VІІІ. Домашнє завдання Опрацювати §2, п.5, виконати вправи №80,83,86,92,97.
Клас. Геометрія Рівень стандарту Хід уроку Варіант 1 1) Трикутник АВF і трапеція АВСD (AB || CD) лежать у різних площинах. Доведіть, що пряма СD паралельна площині АВF. (4 бали) 2) Пряма а паралельна площині a. Доведіть, що в площині a існує пряма, яка мимобіжна прямій а. (8 балів) Варіант 2 1) Трикутник АВК і паралелограм АВСD лежать у різних площинах. Доведіть, що пряма СD паралельна площині АВК. (4 бали) 2) Пряма а паралельна площині a. Доведіть, що в площині a існує пряма, яка паралельна прямій а. (8 балів) Варіант 3 1) Дано куб АВСDА1B1С1D1. Доведіть, що пряма АС паралельна площині А1С1D. (4 бали) 2) Дано мимобіжні прямі а і b. Доведіть, що існує площина, яка містить пряму а і паралельна прямій b. (8 балів) Варіант 4 1) У трикутній піраміді SАВС точки М. і N —.середини ребер SА і SВ, відповідно. Доведіть, що пряма МN паралельна площині АВС. (4 бали) 2) Дано паралельні прямі а і b. Доведіть, що існує площина, яка містить пряму а і паралельна прямій b. (8 балів) Виконання вправ 1. Наведіть приклади паралельних площин із оточення. 2. На моделях куба, прямокутного паралелепіпеда покажіть паралельні та площини, що перетинаються. 3. Користуючись зображенням прямокутного паралелепіпеда АВСDА1B1С1D1, укажіть: а) грані, які перетинають грань АВСD; б) площини, які паралельні площині АВС. 4. Площини a і b паралельні. Доведіть, що кожна пряма площини a паралельна площині b. Ознака паралельності площин Формулюється ознака паралельності площин і проводиться доведення її згідно з підручником. Доречно зробити записи в зошитах.
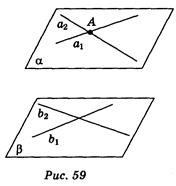
Дано: a 1 Ì a; а 2 Ì a; a 1 і a 2 перетинаються в точці А; b 1 Ì b; b 2 Ì b; a 1 || b 1; а 2 || b 2 (рис. 59). Довести: a || b. Доведення Припустимо, що a і b перетинаються по с. Оскільки a 1 || b 1, то а 1 || b, отже, а 1 || с. Оскільки а 2 || b 2 то а 2 || b, отже, а 2 || с. Через точку А проходять дві прямі а 1 і а 2, які паралельні с, що суперечить аксіомі паралельності. Отже, a || b.
Виконання вправ 1. Дано куб АВСDА 1 В 1 С 1 D 1. Доведіть паралельність площин: а) АВС і А1В1С1; б) АВ1D1 і ВDС1. 2. Точка В лежить поза площиною a. Проведіть через точку В площину, паралельну площині a. 3. Задача № 19 із підручника (с. 19). 4. Доведіть, що площини a і b паралельні, якщо дві прямі а і b, які лежать у площині a і перетинаються, паралельні площині b. 5. Відомо, що дві прямі, які лежать у площині a, паралельні двом прямим площини b. Чи випливає з цього, що a || b? 6. Задача № 20 із підручника (с. 19). III. Домашнє завдання § 34; задачі №98, 104, 113, 136, 148. Академічний рівень Девіз уроку Геометрія — це інтуїція. Г. Гельмгольц ХІД УРОКУ I. Організаційний момент Перевірка домашнього завдання та відповіді на запитання, які виникли в учнів під час його виконання. II. Повідомлення теми та мети уроку III. Актуалізація опорних знань учнів Фронтальне опитування по вивченому раніше. Пригадування основних понять за планом: • основні поняття стереометрії; • аксіоми стереометрії; • різні способи побудови площини; • варіанти розташування прямих на площині. С. Формування вмінь Усні вправи (№217, 218). Письмові вправи (№224, 226, 234, 240). Фронтальне опитування. VІІ. Домашн
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 1036; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.52.243 (0.013 с.) |



 ;
;  ;
;  ;
;  ;
;  ;
; 
 , ширина 3 м, а периметр 20 м;
, ширина 3 м, а периметр 20 м; м, а периметр 20 м.
м, а периметр 20 м. точка
точка  ;
;  ;
;  ? Чому?
? Чому? ;
;  ?
? ;
;  ;
;  ;
;  ?
? Учні спрощують вирази, знаходять відповідь і, перевертаючи «вітамін» зворотною стороною, знаходять відповідну літеру.
Учні спрощують вирази, знаходять відповідь і, перевертаючи «вітамін» зворотною стороною, знаходять відповідну літеру.












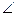 1 =
1 = 

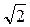 м. Знайдіть площу квадрата.
м. Знайдіть площу квадрата.
 0 (відносно х).
0 (відносно х). (-∞; х 1) і х
(-∞; х 1) і х 
 ), знайомих учням із 7 та 8 класів, на зростання та спадання, а також на проміжки знакосталості. Результати цих досліджень слід зафіксувати як опорні факти і закріпити ці факти на усних та письмових вправах.
), знайомих учням із 7 та 8 класів, на зростання та спадання, а також на проміжки знакосталості. Результати цих досліджень слід зафіксувати як опорні факти і закріпити ці факти на усних та письмових вправах. ; 3) у = -2 х; 4) у =
; 3) у = -2 х; 4) у =  .
. . Доведіть, що:
. Доведіть, що: .
. і переконайтесь, що графіком заданої функції є парабола;
і переконайтесь, що графіком заданої функції є парабола; і
і  вершини параболи; визначте, найбільшого чи найменшого значення набуває функція в точці з координатами (
вершини параболи; визначте, найбільшого чи найменшого значення набуває функція в точці з координатами ( );
); ; якщо так, то знайдіть абсциси точок перетину;
; якщо так, то знайдіть абсциси точок перетину; , де
, де  .
. ;
; б)
б) 
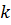 ;
;
 зростає на всій області визначення.
зростає на всій області визначення. спадає на всій області визначення.
спадає на всій області визначення. є непарною при будь-яких
є непарною при будь-яких  .
. ;
; .
.

 Теорема.
Теорема.


