Тема: Симетрія відносно прямої

Мета:

навчальна: формування поняття симетрії відносно прямої; вивчення властивостей симетрії відносно прямої; формування вмінь застосовувати вивчені означення і властивості до розв'язування задач.

розвивальна: розвивати пізнавальні інтереси, уміння запам’ятовувати, працювати в колективі та індивідуально.

виховна: виховувати уважність, акуратність, дисциплінованість, логічне мислення.

Тип уроку: комбінований.

Обладнання: підручники, зошити, таблиця «Перетворення фігур. Рухи» [13].

Література: Геометрія: підручник для 9 класу для загальноосвіт. навч. закл./ Мерзляк А.Г., Полонський В.Б., Якір М.С. – Харків: «Гімназія», 2009.

Хід уроку

І. Перевірка домашнього завдання

Перевірити наявність виконаних домашніх завдань та відпо­вісти на запитання, які виникли в учнів при їх виконанні.

Фронтальна бесіда

1) Дайте означення симетрії відносно точки.

2) Які фігури називаються центрально-симетричними? Наведіть приклади.

3) Укажіть координати точки, яка симетрична точці A (a; b)від­носно початку координат.

ІІ. Сприймання й усвідомлення нового матеріалу

Поняття симетрії відносно прямої

Точки X і X ₁ називаються симетричними відносно прямої l, якщо пряма l є серединним перпендикуляром до відрізка ХХ ₁(рис. 163), тобто якщо ОХ = ОХ ₁і l XX ₁.

Перетворення фігури F на фігуру F ₁, при якому кожна точ­ка X фігури F переходить у точку Х ₁фігури F ₁, симетричну їй відносно даної прямої l, називається перетворенням симетрії відносно прямої l або осьовою симетрією (рис. 164). При цьо­му фігури F і F ₁називаються симетричними відносно прямої l, а пряма l — віссю симетрії.

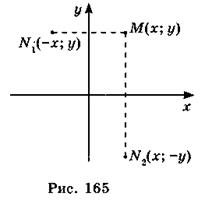
Властивості осьової симетрії

1) Перетворення осьової симетрії є переміщенням.

2) Осьова симетрія перетворює пряму на пряму; відрізок — на відрізок; многокутник — на рівний йому многокутник.

3) Точки, що належать осі симетрії, відображаються самі на себе.

4) Якщо точки М (х; у)і N (x ₁; y ₁) симетричні (рис. 165) від­носно:

а) осі Ох, то виконується умова

б) осі Оу, то виконується умова

Якщо перетворення симетрії відносно прямої l переводить фігуру F у себе, то ця фігура називається симетричною відносно прямої l, а пряма l — називається віссю симетрії (рис. 166).

Виконання вправ

1. Побудуйте довільний трикутник ABC і симетричний йому трикутник відносно осі:

а) АВ; б) ВС.

2. Скільки осей симетрії має:

а) коло;

б) прямокутник;

в) квадрат;

г) ромб;

д) рівносторонній трикутник?

 

ІІІ. Закріплення й осмислення нового матеріалу

Розв'язування задач

1. Побудуйте довільний трикутник і трикутник, симетричний даному, відносно прямої, якщо вона:

а) розміщена поза трикутником;

б) має лише одну спільну точку з трикутником;

в) перетинає дві сторони трикутника.

2. Чотирикутник ABCD заданий координатами своїх вершин: А (1; 1); В (-3; 2), С (-1; -2), D (5; -3). Знайдіть координати вершин чотирикутника, який симетричний даному відносно осі: а) Ох; б) Оу.

3. Доведіть властивості симетрії відносно прямої.

4. Запишіть рівняння кола, яке симетричне колу (х – 1)² +(у + 2)² = 1 відносно:

а) осі Ох; б) осі Оу.

5. Запишіть рівняння прямої, яка симетрична прямій х + у = 1 відносно:

а) осі Ох; б) осі Оу.

6. Дано пряму MN і точки А і В в різних півплощинах віднос­но MN і на різній відстані від неї. Через точки А і В проведіть прямі так, щоб кут між ними ділився прямою MN навпіл.