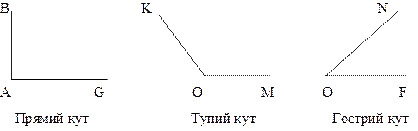Отримання геометричної фігури

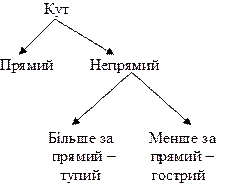
В процесі роботи з багатокутниками учні отримають перші відомості про кути (кут створюють дві сторони багатокутника, які виходять з однієї вершини),й вчаться показувати кути багатокутника. З цією метою виконуються вправи: паперовий багатокутник розривається на частини так, щоб кожна з них містила по 1 вершині та по 2 сторони (частини сторін),які виходять з цієї вершини; звертається увага дітей на те що вершина багатокутника є й вершиною відповідного кута. Спочатку знайомимо дітей з паперовими моделями кутів. Діти повинні виготовити їх, розірвавши паперовий багатокутник.

Ілюстрація: кут столу, дошки та ін.

Властивості: величина кута не залежить від довжини його сторін, а залежить від взаємного розташування його сторін.

Виділення фігури, що вивчається, із множини інших фігур: тут ми показуємо кути багатокутників.

Побудова геометричної фігури: ставимо крапку – це вершина кута й креслимо два промені, які мають спільний початок (цю точку) – це сторони кута.

Після цього показуємо отримання прямого кута перегинанням аркушу паперу “неозначеної” форми:

Учні беруть аркуш паперу й складають його удвічі, лінія згину розгладжується, аркуш розгортається; діти впевнюються, що лінія згину – пряма. Ще раз по лінії згину перегинаємо аркуш – отримаємо модель прямого кута. Розгортаємо аркуш й показуємо учням, що дві лінії, що перетинаються ділять аркуш на 4 частини – на 4 кути. Вершина цих кутів – 1 крапка. Всі ці кути рівні(порівнюємо кути, які отримано різними учнями). Ці кути називаються прямими.

Після цього порівнюємо непрямі та прямі кути з моделлю прямого кута. При накладенні звертаємо увагу, щоб вершини і одна із сторін обох кутів збігалися.

У подальшому для встановлення виду кута використовують прямий кут креслярського трикутника, якщо кути збігаються (тобто збігаються їх сторони і вершини), тоді цей кут є прямим, якщо ні – не прямий.

Для закріплення уявлень про прямий кут пропонуємо вправи:

1) серед даних кутів знайти прямі кути:

2) у даних багатокутників знайти прямі кути:

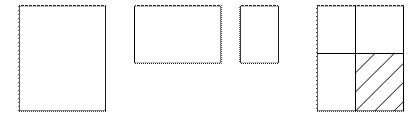
3) накреслити прямий кут у зошиті, використовуючи розліновку зошиту.

4) накреслити трикутник (чотирикутник),який має прямий кут.

Доцільно поряд з паперовими моделями кута використовувати модель “розсувного кута” – малку, Її можливо виготовити із двох паличок, що скріплені гвіздком. За допомогою такої моделі діти наочно впевнюються що величина кута залежить не від довжини його сторін, а від взаємного розташування сторін відносно одне одного.

Поняття кута закріпляється при розгляданні прямокутника. Поняття “прямокутник” та “квадрат” розглядаються за планом:

- пропонуємо набір геометричних фігур й засобом виключення зайвих фігур залишаємо фігури, що вивчаються;

- вводимо означення фігури;

- ілюстрація;

- властивості;

- задачі на побудову.

Прямокутник

Пропонуємо набір геометричних фігур й засобом виключення зайвих фігур залишаємо фігури, що вивчаються.

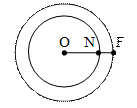
§ Уважно розгляньте фігури. Яку фігуру можна виключити? Чому?

§ Як одним словом можна назвати решту фігур? (чотирикутники)

§ Знайдіть чотирикутник, у якого немає прямого кута (за допомогою креслювального трикутника). (2, 3)

§ Знайдіть чотирикутник, у якого є тільки один прямий кут (1). Виключимо його, що можна сказати про решту чотирикутників? (в цих чотирикутниках більш ніж один прямий кут).

§ Знайдіть чотирикутник, у якого тільки два прямих кута (4). Виключимо його, що можна сказати про решту чотирикутників?(в цих чотирикутниках більш ніж два прямих кута).

§ Що можна сказати про решту чотирикутників? (5, 6, 7) Скільки в них прямих кутів? (в них всі кути прямі!)

§ Такі фігури називаються прямокутниками.

Вводимо означення фігури: (родове поняття – чотири­кут­ник, видове поняття – прямі кути)

Означення: чотирикутник, у якого всі кути прямі називається прямокутником.

Ілюстрація: знайдіть у оточуючій обстановці предмети прямокутної форми.

§ Покажіть прямокутники серед геометричних фігур.

§ Виріжте з паперу в клітинку прямокутник.

Властивості: Дітям пропонується набір геометричних фігур, які вирізані з аркушу:

§ Візьміть в руки прямокутник. Порівняйте за довжиною його протилежні сторони – ті, що лежать напроти одна одної. Використовуйте прийом накладання.

§ Що цікавого ви помітили? (у прямокутника протилежні сторони попарно рівні).

§ Перевіримо це ствердження таким чином: виміряйте та запишіть довжину кожної сторони синього прямокутника (у кожного учня різні сині прямокутники).

§ Назвіть отримані результати вимірювання (вчитель їх записує на дошці)Уважно подивіться на результати вимірювання. Який можна зробити висновок? (у прямокутника протилежні сторони рівні)

§ Візьміть червоний прямокутник (червоні прямокутники – різні квадрати).Виміряйте довжину його сторін й назвіть отримані результати (вчитель записує їх на дошці).

§ Що цікавого ви помітили? (є такі прямокутники, у котрих не тільки по дві протилежні сторони рівні, а ще є й такі, у яких всі сторони рівні, але взагалі про них теж можна сказати, що в них протилежні сторони рівні.)

Задачі на побудову.

Квадрат

Пропонуємо набур геометричних фігур й засобом виключення зайвих фігур залишаємо фігури, що вивчаються.

§ Які фігури зображено на малюнку? (прямокутники)

§ Виміряйте сторони прямокутників. Чи треба виконувати чотири вимірювання? Чому?

§ Що цікавого ви помітили?(серед прямокутників знаходяться й такі, у яких всі сторони рівні між собою)

§ Такі прямокутники називаються квадратами.

Вводимо означення фігури:

Означення: прямокутник, у якого всі сторони рівні називається квадратом.

Тобто квадрат – це взагалі прямокутник, але не звичайний, а такий що має усі рівні сторони (Родове поняття прямокутник, а видове – всі сторони рівні).

Ілюстрація;

Властивості: всі сторони рівні і всі кути рівні.

§ Покажи прямокутники, які не можна назвати квадратами.

§ Про кожний квадрат можна сказати, що він прямокутник. Чи можна, навпаки, про кожний прямокутник сказати, що він квадрат?

§ Домалюй цю фігуру, щоб отримати квадрат.

Задачі на побудову.

Коло. Круг

§ Серед геометричних фігур є круги (вчитель показує модель круга).Багато предметів мають форму круга. Назвіть такі предмети.

§ Як можна зобразити круг на папері? (взяти й обвести блюдце й тощо).Але це незручно, адже круги потрібні різні. Для цього користуються інструментом – циркулем.

§ Візьміть циркуль. Поставимо першу ніжку (з гострим кінцем) на аркуш паперу – це буде центр кола, а другою ніжкою циркуля опишімо круг. Ми отримали коло. Лінія, яку креслить циркуль, називається колом. Коло є межею круга. З чого можна зробити модель кола? (з ниток, дроту) З чого можна зробити модель круга? (вирізати з паперу й тощо)

У круга есть одна подруга,

Знакома всем ее наружность!

Она идет по краю круга

И назвается – окружность.

§ Коли ми креслимо коло циркулем, то його голка повинна весь час знаходитися в одній точці – центрі кола. Тепер поставимо на колі дві будь-які дві точки й з’єднаємо їх почергово з центром кола. Виміряйте довжину отриманих відрізків. Назвіть результати вимірювання.(вчитель записує їх на дошці).Уважно розгляньте отримані результати вимірювання. Що цікавого ви помітили?(у кожному випадку вимірювання відрізки є рівними)

§ Який можна зробити висновок? (якщо ми з’єднаємо центр кола з будь якими точками на колі, то ми отримаємо рівні відрізки) Відрізки, що з’єднують центр кола з будь-якою точкою кола називаються радіусами кола.

Радіус – це відрізок, який з’єднує центр кола з будь-якою точкою кола.

У підручнику центр кола позначається буквою О, а радіус – ОА.

Можливі вправи:

1) покажи 2 круга різного кольору; різного радіусу (серед кількох на дошці). Який з них більший – зелений чи червоний? У якого круга радіус більший?

2) у цих кіл спільний центр. Накреслити кілька кіл з спільним центром. Де в навколишньому світі ви зустрічали кілька кіл з спільним центром (круги на воді після падіння каменя).

3) побудуй коло, проведи в ньому радіус; скільки радіусів можна провести?

4) накреслити коло з радіусом 2 см.

Робота над завданням

1. Малюємо ескіз від руки й намітимо шляхи розв’язання:

2. Будуємо за допомогою циркуля та лінійки:

- креслимо відрізок довжиною 2 см;

- встановлюємо ніжки циркуля на кінці цього відрізку;

- проводимо коло, відмічаємо центр кола.

3. Доведення: проводимо радіус отриманого кола, вимірюємо його. Отримали – 2 см. Тому ми побудували коло, що вимагалося.

4. Дослідження: якщо б ми не задали довжину радіусу – 2 см, а просто б попросили накреслити коло, скільки б було розв’язків? (багато).

- Ми побудували коло з радіусом 2 см. Тепер розмалюйте круг з цим же радіусом. Відмітимо точки, що лежать у крузі та поза кругом, на колі.