
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Під час руху плоскої фігури рухома центроїда котиться по нерухомій без ковзання.Содержание книги
Поиск на нашем сайте
Це окремий випадок більш загальної теореми Пуансо, яку розглянемо, вивчаючи обертання твердого тіла навколо нерухомої точки. Нарешті зауважимо, що плоскопаралельний рух розглядали як окремий випадок руху вільного твердого тіла. Отже, для цього випадку також справедлива доведена теорема про проекції двох точок тіла на пряму, що проходить через ці точки.
План швидкостей
Розглянемо графічний метод визначення швидкостей різних точок плоскої фігури. Це метод побудови плану швидкостей. Визначимо швидкості всіх точок фігури
Скористаємося формулами (2.73) і (2.74). Насамперед визначимо швидкість точки В, траєкторія якої відома. Виберемо полюс у точці А. Тоді
Побудуємо цю векторну рівність. Вектор
Щоб визначити швидкість довільної точки С, з’єднаємо її з точками А та В. Виберемо полюс по черзі в точках А та В. Маємо
Швидкість точки С невідома; швидкості точок А та В повністю відомі; вектори Як видно з побудови, Тепер легко знайти швидкість будь-якої точки плоскої фігури. Наприклад, щоб знайти швидкість точки М, яка знаходиться на прямій АВ (рис. 2.31, б) визначимо відповідну їй Положення точки
Із плану швидкостей можна визначити також миттєву кутову швидкість.
2.2.9. Розподіл прискорень точок при плоскопаралельному русі
Прискорення довільної точки тіла при плоскопаралельному русі можна знайти з виразу (2.65):
Як зазначалось, вектори
оскільки Отже,
де
Рисунок 2.32
Векторна сума обертального і доцентрового прискорення є прискоренням обертального руху точки плоскої фігури навколо полюса:
Формулу (2.77) можна записати у вигляді
Отже, Прискорення довільної точки тіла при плоскопара-лельному русі дорівнює векторній сумі прискорення полюса і прискорення обертального руху точки навколо полюса. З’ясуємо деякі властивості прискорення обертального руху плоскої фігури навколо полюса. Розглянемо кут Цей кут завжди гострий, бо в противному разі доцентрове прискорення було б напрямлене від полюса, що неможливо. Величину цього кута знайдемо з формули
З формули (2.80) видно, що кут Нарешті, модуль вектора
Рисунок 2.33 Миттєвий центр прискорень
У тих випадках, коли
Отже, вектор прискорення
Розглянемо два способи побудови миттєвого центра прискорень. Спосіб 1. Нехай відоме прискорення
Рисунок 2.34 Відкладаючи від Спосіб 2. Припустимо, що відомі прискорення
Рисунок 2.35 Побудувавши Знаючи положення миттєвого центра прискорень та прискорення однієї точки плоскої фігури, можна побудувати напрями і знайти величини прискорень довільних її точок. Наприклад, прискорення точки Зауважимо, що вираз (2.82) дає змогу встановити зв’язок між прискореннями точок плоскої фігури:
Отже, побудова миттєвого центра прискорень дозволяє повністю вирішити питання про розподіл прискорень точок при плоскопаралельному русі твердого тіла.
Приклади
Приклад 2.5. Розглянемо приклад застосування викладених вище способів визначення розподілу швидкостей у плоскій фігурі. Механізм, зображений на рис. 2.36, складається з кривошипа
Рисунок 2.36 Розв’язання. Кутову швидкість шатуна, що здійснює плоскопаралельний рух, можна знайти, якщо відомі швидкості його точок. Точка
Швидкість точки
Таким чином,
Цей самий результат можна дістати, якщо скористатися теоремою про проекції швидкостей двох точок тіла на пряму, що з’єднує ці точки. Маємо
Для визначення швидкості точки
Звідси
Елементарні геометричні розрахунки дають змогу визначити
Приклад 2.6. Розглянемо застосування теореми про розподіл прискорень у тілі при плоскопаралельному русі. У механізмі, зображеному на рис. 2.37, кривошип
Рисунок 2.37 Розв’язання. Згідно з (2.79) прискорення довільної точки плоскої фігури складається з прискорення полюса і прискорення обертального руху точки навколо полюса. Полюс слід вибирати в точці, прискорення якої відоме, або його легко визначити з умови задачі. Такою точкою є точка А, швидкість якої
Щоб знайти прискорення
де Тут З умови кочення без ковзання випливає, що швидкість точки Тоді миттєва кутова швидкість
і миттєве кутове прискорення
Отже, Таким чином, прискорення точки
Вектор
2.2.11. Додавання обертальних рухів тіла навколо осей, Розглянемо додавання двох миттєвих обертальних рухів твердого тіла навколо осей, що перетинаються. Припустимо, що тіло обертається навколо осі Доведемо лему про додавання кутових швидкостей. В результаті додавання двох миттєвих обертальних рухів тіла навколо осей, що перетинаються, результуючим є абсолютний миттєвий обертальний рух навколо осі, яка проходить через точку перетину осей складових обертань.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.19.29 (0.009 с.) |

 (рис. 2.31), якщо відомі вектор швидкості
(рис. 2.31), якщо відомі вектор швидкості  точки А і те, що вектор
точки А і те, що вектор  напрямлений вздовж прямої
напрямлений вздовж прямої  (рис. 2.31, а).
(рис. 2.31, а). а
а
 б
б
 .
. спрямований вздовж
спрямований вздовж  ,
,  паралельного
паралельного  – перпендикулярною до АВ (рис. 2.31, б). Дістаємо
– перпендикулярною до АВ (рис. 2.31, б). Дістаємо .
.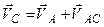 ;
; .
.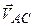 і
і 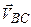 перпендикулярні до АС і ВС відповідно. Розв’язуємо графічно систему векторних рівнянь. На плані швидкостей через точки а і
перпендикулярні до АС і ВС відповідно. Розв’язуємо графічно систему векторних рівнянь. На плані швидкостей через точки а і  проводимо прямі, паралельні швидкостям
проводимо прямі, паралельні швидкостям  . На перетині прямих
. На перетині прямих  і
і  знаходимо точку с – кінець вектора
знаходимо точку с – кінець вектора  . З’єднаємо точку С з точкою Р. Швидкість точки С побудована (
. З’єднаємо точку С з точкою Р. Швидкість точки С побудована ( ).
). на плані швидкостей подібний до
на плані швидкостей подібний до 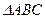 плоскої фігури і повернутий відносно нього на кут
плоскої фігури і повернутий відносно нього на кут  .
. на плані швидкостей, з’єднаємо цю точку з полюсом Р. Відрізок
на плані швидкостей, з’єднаємо цю точку з полюсом Р. Відрізок  – швидкість точки М.
– швидкість точки М.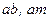 на плані швидкостей є швидкостями обертального руху
на плані швидкостей є швидкостями обертального руху 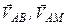 . Відомо, що
. Відомо, що 
 . Тому для визначення положення точки
. Тому для визначення положення точки  .
. .
. . (2.76)
. (2.76) і
і  перпендикулярні до площини руху фігури, тому на підставі властивостей подвійного векторного добутку перепишемо третій доданок у правій частині (2.76):
перпендикулярні до площини руху фігури, тому на підставі властивостей подвійного векторного добутку перепишемо третій доданок у правій частині (2.76): ,
,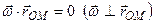 .
. , (2.77)
, (2.77) – прискорення полюса
– прискорення полюса  ;
;  – обертальне прискорення;
– обертальне прискорення;  – доцентрове прискорення (рис. 2.32).
– доцентрове прискорення (рис. 2.32).
 ;
;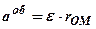 ; (2.78)
; (2.78) .
. . (2.79)
. (2.79) між вектором
між вектором  і вектором
і вектором  .
. . (2.80)
. (2.80) не залежить від вибору полюса і є однаковим для всіх точок тіла в даний момент часу. Цей кут відліковується від
не залежить від вибору полюса і є однаковим для всіх точок тіла в даний момент часу. Цей кут відліковується від 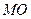 (рис. 2.33) у напрямі обертання плоскої фігури, якщо
(рис. 2.33) у напрямі обертання плоскої фігури, якщо  . (2.81)
. (2.81)
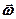 і
і  одночасно не дорівнюють нулеві, можна знайти таку точку плоскої фігури, вектор прискорення якої в даний момент часу дорівнює нулеві. Цю точку
одночасно не дорівнюють нулеві, можна знайти таку точку плоскої фігури, вектор прискорення якої в даний момент часу дорівнює нулеві. Цю точку  називають миттєвим центром прискорень. Якщо полюсом обрати миттєвий центр прискорень, то прискорення кожної точки плоскої фігури можна розглядати як прискорення обертального руху навколо миттєвого центра прискорень
називають миттєвим центром прискорень. Якщо полюсом обрати миттєвий центр прискорень, то прискорення кожної точки плоскої фігури можна розглядати як прискорення обертального руху навколо миттєвого центра прискорень  , тобто
, тобто  . Оскільки
. Оскільки 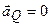 , то
, то .
.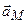 довільної точки
довільної точки  утворює визначений за (2.80) кут
утворює визначений за (2.80) кут  . (2.82)
. (2.82) точки
точки 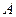
 , що утворює з вектором
, що утворює з вектором 
 двох точок
двох точок 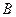 плоскої фігури (рис. 2.35). Щоб знайти миттєвий центр прискорень
плоскої фігури (рис. 2.35). Щоб знайти миттєвий центр прискорень  .
.
 (рис. 2.35), визначимо кут
(рис. 2.35), визначимо кут  . Проведемо з точок
. Проведемо з точок  , що утворюють кут
, що утворюють кут 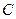 знаходимо, з’єднавши точку
знаходимо, з’єднавши точку  .
. .
.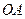 , який обертається навколо осі
, який обертається навколо осі  рад/с. Зубчасте колесо радіусом
рад/с. Зубчасте колесо радіусом  20 см котиться без ковзання по поверхні нерухомого колеса радіусом
20 см котиться без ковзання по поверхні нерухомого колеса радіусом  см і приводить до руху з’єднаний з ним шарнірно шатун
см і приводить до руху з’єднаний з ним шарнірно шатун  см. Повзун С рухається вздовж вертикалі. Визначити кутову швидкість шатуна і швидкості точок
см. Повзун С рухається вздовж вертикалі. Визначити кутову швидкість шатуна і швидкості точок  перпендикулярний до кривошипа
перпендикулярний до кривошипа 
 зчеплення рухомого і нерухомого коліс є миттєвим центром швидкостей рухомого колеса. Отже,
зчеплення рухомого і нерухомого коліс є миттєвим центром швидкостей рухомого колеса. Отже, .
. см/с.
см/с. см/с.
см/с. , або
, або  .
. . Він знаходиться в точці
. Він знаходиться в точці  перетину прямих
перетину прямих  і
і  , перпендикулярних до векторів швидкостей точок
, перпендикулярних до векторів швидкостей точок  .
.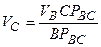 .
.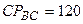 см,
см,  см. Тоді
см. Тоді см/с;
см/с; рад/с.
рад/с. навколо нерухомої осі
навколо нерухомої осі  колеса ІІ.
колеса ІІ.
 . Прискорення точки А дорівнює тільки нормальному прискоренню і напрямлене від точки
. Прискорення точки А дорівнює тільки нормальному прискоренню і напрямлене від точки  .
. , згадаємо, що
, згадаємо, що ,
, ;
;  .
. і
і  – миттєва кутова швидкість і миттєве кутове прискорення колеса ІІ, які треба визначити.
– миттєва кутова швидкість і миттєве кутове прискорення колеса ІІ, які треба визначити.
 .
. .
. , напрямлених уздовж спільної прямої в одну сторону. Додаючи їх, маємо
, напрямлених уздовж спільної прямої в одну сторону. Додаючи їх, маємо .
. напрямлений уздовж прямої
напрямлений уздовж прямої 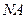 від точки
від точки 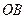 з миттєвою кутовою швидкістю
з миттєвою кутовою швидкістю 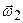 , а разом з віссю
, а разом з віссю  (рис. 2.41). Також припускаємо, що дві вказані осі перетинаються в точці
(рис. 2.41). Також припускаємо, що дві вказані осі перетинаються в точці 


