
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Швидкістю точки називають фізичну величину, що характеризує зміну положення точки в просторі, що визначається радіусом-вектором, зі зміною часу.
При векторному способі визначення руху точки закон її руху має вигляд
Траєкторія точки – годограф функції На основі визначення поняття швидкості і фізичного змісту похідної векторної функції скалярного аргумента робимо висновок, що швидкість точки є вектор, який дорівнює похідній за часом
Вектор швидкості напрямлений по дотичній до годографа вектора Рівність (2.15) визначає вектор швидкості точки векторним способом математичного опису її руху. Розглянемо визначення швидкості координатним способом. З рівностей (2.7) і (2.15) маємо
Розкладаючи вектор
і порівнюючи вирази, маємо
За відомими проекціями вектора швидкості на координатні осі, легко знайти модуль вектора швидкості і його напрямні косинуси:
Рівності (2.16)-(2.18) визначають вектор швидкості точки координатним способом математичного опису її руху. Знайдемо швидкість, припускаючи, що рух точки задано натуральним способом. Розглядаючи радіус-вектор точки як складну функцію часу, згідно рівностей (2.8), (2.10) і (2.15) дістанемо
З’ясуємо зміст кожного співмножника останньої рівності. Розглянемо вектор
На підставі змісту підрозділу 2.1.3 твердимо, що цей вектор напрямлений по дотичній до траєкторії у бік додатних дугових координат. Справді, якщо
оскільки
Рисунок 2.7 Отже, На підставі викладеного дістанемо
Щоб визначити
Отже,
Рівності (2.20)-(2.22) визначають вектор швидкості точки натуральним способом математичного опису її руху.
Прискорення руху точки Прискорення – це фізична величина, що характеризує зміну вектора швидкості руху точки за часом.
На підставі цього означення і змісту підрозділу 2.1.3 можна визначити величину і напрям прискорення точки:
Вектор Знайдемо прискорення точки трьома способами опису її руху. Якщо рух точки задано векторним рівнянням
то швидкість
Для визначення прискорення точки координатним способом скористаємося рівностями (2.7) і (2.24):
Розкладаючи вектор прискорення
і порівнюючи вирази, маємо
Модуль вектора
Формули (2.25)-(2.27) визначають вектор прискорення координатним способом. Знайдемо прискорення точки, користуючись натуральним способом. Із (2.22) і (2.23) дістанемо
Зауважимо, що орт
Розглянемо похідну від
Знайдемо напрям вектора Вектор Якщо Зауважимо, що всі точки будь-якої плоскої кривої лежать у стичній площині. З рис. 2.8 видно, що вектор
Рисунок 2.8 Визначимо модуль вектора
З трикутника MNK (рис. 2.8) знаходимо
тому
Оскільки
де
Позначимо орт головної нормалі через
Побудуємо місцевий координатний базис – натуральний тріедр (рис. 2.9). Орти дотичної і головної нормалі створюють стичну площину кривої. Проведемо нормаль до цієї площини. Цю нормаль називають бінормаллю, її орт Повернемось до визначення прискорення точки. На підставі (2.29) і (2.31) вираз (2.28) набуває вигляду
Зауважимо, що Розкладемо вектор
і порівняємо отриманий вираз із формулою (2.32):
Як видно з (2.33), (2.34), проекція вектора прискорення на бінормаль дорівнює нулеві. Отже, вектор прискорення точки лежить завжди у стичній площині траєкторії точки. Проекцію Повне прискорення точки є векторною сумою дотичного і нормального прискорень (рис. 2.10).
Модуль прискорення і його напрям:
Отже, формули (2.33), (2.34), (2.35) визначають вектор прискорення натуральним способом.
Приклади Приклад 2.1. Рівнозмінний рух точки. Рух точки називають рівнозмінним, якщо її дотичне прискорення стале ( Знайдемо швидкість точки і закон її руху по траєкторії. На підставі (2.34)
звідки За формулою (2.21)
звідки після інтегрування маємо
де У даному випадку початковими умовами є початкова швидкість і початкова дугова координата. Нехай
Дістанемо:
Приклад 2.2. Рух точки відбувається згідно з рівняннями
( Визначити: — швидкість точки; — закон руху точки по траєкторії; — годограф швидкості; — прискорення точки; — радіус кривини траєкторії точки. Розв’язання. Виберемо систему координат, як показано на рис. 2.11. Складові швидкості точки дорівнюють:
Модуль швидкості
Рисунок 2.11 Траєкторією точки є гвинтова лінія. Напрям швидкості, тобто напрям дотичної до гвинтової лінії (рис. 2.11), визначаємо за формулами
Годограф швидкості знаходимо на підставі формул
Звідси Отже, годографом швидкості є коло радіуса Знайдемо закон руху точки по траєкторії
Рисунок 2.12
При
Для визначення проекцій, модуля та напряму прискорення скористаємося формулами (2.25)-(2.27). Маємо:
Вектор прискорення лежить в горизонтальній площині і спрямований від точки М до осі Радіус кривини точки знаходимо на підставі (2.34). Нормальне прискорення визначаємо через повне і тангенціальне за формулами (2.34) і (2.35):
Оскільки
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.48.62 (0.05 с.) |
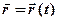 .
.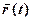 .
. від радіуса-вектора:
від радіуса-вектора: . (2.15)
. (2.15) Тут і далі диференціювання за часом позначено крапкою.
Тут і далі диференціювання за часом позначено крапкою.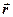 , тобто по дотичній до траєкторії точки в той бік, що відповідає зростанню часу
, тобто по дотичній до траєкторії точки в той бік, що відповідає зростанню часу  .
. по ортах ортогональної системи декартових координат
по ортах ортогональної системи декартових координат
 . (2.16)
. (2.16) ; (2.17)
; (2.17)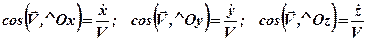 . (2.18)
. (2.18) .
.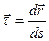 . (2.19)
. (2.19) , то вектор
, то вектор  напрямлений у бік додатних дугових координат
напрямлений у бік додатних дугових координат  (рис. 2.7). У цей самий бік напрямлений і вектор
(рис. 2.7). У цей самий бік напрямлений і вектор  . Зі зміною знака
. Зі зміною знака  змінюється і знак
змінюється і знак  ,
,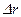 є довжиною хорди
є довжиною хорди  (рис. 2.7).
(рис. 2.7).
 . (2.20)
. (2.20) , домножимо рівність (2.20) скалярно на вектор
, домножимо рівність (2.20) скалярно на вектор  . (2.21)
. (2.21) . (2.22)
. (2.22) . (2.23)
. (2.23)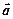 напрямлений по дотичній до годографа вектора швидкості
напрямлений по дотичній до годографа вектора швидкості  .
.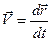 , і на підставі (2.23) прискорення
, і на підставі (2.23) прискорення . (2.24)
. (2.24) .
. по ортах декартової системи координат
по ортах декартової системи координат
 . (2.25)
. (2.25) ; (2.26)
; (2.26) .(2.27)
.(2.27)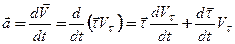 . (2.28)
. (2.28) . Отже,
. Отже,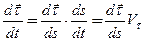 . (2.29)
. (2.29) .
.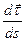 і його модуль.
і його модуль. . Щоб його побудувати, проведемо одиничні вектори
. Щоб його побудувати, проведемо одиничні вектори  в сусідніх точках М і
в сусідніх точках М і  , де
, де  . Побудуємо в точці М вектор
. Побудуємо в точці М вектор  , що дорівнює
, що дорівнює  .
. , точка
, точка  , то площина трикутника
, то площина трикутника  , обертаючись навколо вектора
, обертаючись навколо вектора 
 .
. , оскільки
, оскільки ,
, .
.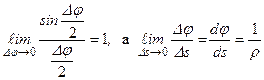 ,
, – радіус кривини кривої, то
– радіус кривини кривої, то . (2.30)
. (2.30) і напрямимо його в бік угнутості кривої. Тоді
і напрямимо його в бік угнутості кривої. Тоді . (2.31)
. (2.31) . У площині (
. У площині ( ) розміщені всі нормалі до кривої, тому орти (
) розміщені всі нормалі до кривої, тому орти (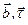 ) утворюють спрямну площину кривої.
) утворюють спрямну площину кривої. . (2.32)
. (2.32) , де
, де 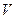 – модуль швидкості.
– модуль швидкості. (2.33)
(2.33) . (2.34)
. (2.34) називають дотичним, або тангенціальним прискоренням, проекцію
називають дотичним, або тангенціальним прискоренням, проекцію  – доцентровим або нормальним прискоренням.
– доцентровим або нормальним прискоренням. .
.

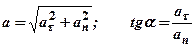 . (2.35)
. (2.35) ).
). ,
, .
.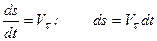 ,
, ,
, і
і  – сталі інтегрування, що знаходяться з початкових умов.
– сталі інтегрування, що знаходяться з початкових умов. .
. ; (2.36)
; (2.36) . (2.37)
. (2.37)
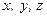 – в метрах,
– в метрах, 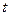 – в секундах).
– в секундах). – початкове положення точки на траєкторії.
– початкове положення точки на траєкторії. .
. .
.


 .
. .
. – рівняння годографа швидкості (рис. 2.12).
– рівняння годографа швидкості (рис. 2.12). з центром в точці
з центром в точці  на осі
на осі 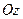 .
. :
:
 .
. , тобто
, тобто  .
. .
.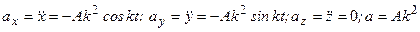 ;
; .
. .
. а
а  , то
, то  . Знаходимо
. Знаходимо .
.


