
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кінематика – це розділ класичної механіки, в якому вивчають геометричні властивості механічних рухів незалежно від фізичних факторів, що спричиняють ці рухи, тобто незалежно від сил.Содержание книги
Поиск на нашем сайте
Кінематика безпосередньо спирається на основні положення геометрії. До цих положень приєднується поняття про час. Кінематику називають також “геометрією рухів”. Рух тіл кінематика вивчає відносно певних систем координат. Ці системи координат вважатимемо рухомими або умовно нерухомими залежно від конкретних умов механічної задачі. Системи координат називають також системами відліку. Основне завдання кінематики – вивчення законів руху матеріальних об’єктів (точок, систем точок, твердих тіл). Закон руху точки або тіла визначається зв’язком між довільним положенням точки чи тіла в просторі з часом. Кінематику поділено на кінематику точки і кінематику абсолютно твердого тіла. Законом руху матеріальної точки називають спосіб її переходу з одного довільного положення у просторі й часі в інше довільне положення.
Способи визначення руху точки
Рух точки в просторі визначається трьома основними способами: векторним, координатним і натуральним. Векторний спосіб найчастіше застосовують в різних теоретичних дослідженнях. Виберемо в просторі умовно нерухому точку О, відносно якої маємо дослідити рух точки М (рис. 2.1). Проведемо з точки О в точку М радіус-вектор
Рівняння (2.1) визначає положення точки в просторі в довільний момент часу. Отже, воно визначає закон руху Розглянемо координатний спосіб. Визначимо поло-ження точки, застосовуючи ортогональну нерухому систему декартових координат
Рисунок 2.2 Функціональні залежності (2.2) називають кінематичними рівняннями руху точки. Вони дають змогу визначити положення точки в просторі в довільний момент часу, тобто є законом руху точки. З аналітичної геометрії відомо, що (2.2) – це рівняння кривої, вздовж якої рухається точка, тобто рівняння траєкторії точки в параметричній формі. Щоб знайти рівняння траєкторії точки в координатній формі, досить з цих рівнянь вилучити параметр
Два останні рівняння (2.3) визначають траєкторію точки як лінію перетину двох циліндричних поверхонь, що проектують траєкторію на координатні площини Крім декартової, користуються й іншими системами координат: на площині – полярною системою координат (
Легко встановити зв’язок між векторним і координатним способами визначення руху точки. Проведемо з початку координат у точку М радіус-вектор
Як відомо, координати точки М дорівнюють проекціям радіуса-вектора
Підставивши (2.6) в (2.5), дістанемо
Залежність (2.7) установлює зв’язок між векторним і координатним способами визначення руху точки.
Натуральним способом визначення руху точки користувався ще Л.Ейлер [ 5 ]. Припустимо, що траєкторія АВ точки М відома (рис. 2.3). Виберемо фіксовану точку О на траєкторії як початкову. Умовимося вважати один напрям від початкової точки О вздовж траєкторії додатним, а протилежний – від’ємним. Положення точки на траєкторії визначимо довжиною дуги
Рівняння (2.8) називають законом руху точки по траєкторії. Закон руху точки в просторі визначається сукупністювсіх даних: траєкторією точки, положенням початкової точки О, додатним і від’ємним напрямами відліку і рівнянням (2.8). Натуральний спосіб визначення руху точки в просторі застосовують і в різних теоретичних дослідженнях, і при розв’язуванні конкретних задач. Особливо доцільно його застосовувати, коли відомі форма і положення в просторі траєкторії точки. Розглянемо поняття про шлях, який проходить точка М. Зауважимо, що слід розрізняти дугову координату
Зрозуміло, що шлях є монотонно зростаючою функцією часу. Звичайно, між натуральним способом визначення руху точки і першими двома способами існує зв’язок. Не вдаючись до подробиць, зауважимо, що радіус-вектор точки
Зв’язок між натуральним і координатним способами визначення руху легко знайти, обчислюючи за відомими формулами диференціальної геометрії елемент дуги
Вибір знака кореня відповідає вибору додатнього напряму відліку дугової координати при незмінному напрямі руху точки по траєкторії.
Годограф векторної функції
Введемо поняття годографа функції
годографом векторної функції Щоб знайти рівняння годографа в параметричному вигляді, досить вибрати довільну ортогональну систему координат Рівняння
є скалярними рівняннями годографа векторної функції Розглянемо похідну від функції
якщо границя в правій частині (2.14) існує. Доведемо, що похідна Розглянемо приріст аргумента
Рисунок 2.5 Як відомо, похідна від скалярної функції визначає напрям дотичної до графіка функції, а її фізичний зміст полягає у визначенні зміни функції залежно від зміни аргумента. Отже, фізичний зміст похідної векторної функції можна вважати аналогічним – похідна векторної функції
Швидкість руху точки
Перейдемо до вивчення основних кінематичних величин, що характеризують рух точки в просторі. Такими величинами є швидкість точки та її прискорення. Як і в підрозділі 2.1.2, скористаємось трьома способами визначення руху точки.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.170.65 (0.008 с.) |

 . Криву, по якій рухається точка, називають її траєкторією. Зі зміною положення точки М на траєкторії відповідно змінюється вектор
. Криву, по якій рухається точка, називають її траєкторією. Зі зміною положення точки М на траєкторії відповідно змінюється вектор 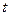 відповідає певне значення радіуса-вектора
відповідає певне значення радіуса-вектора 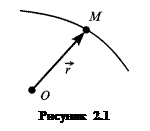
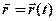 . (2.1)
. (2.1) (рис. 2.2). Координати точки
(рис. 2.2). Координати точки  однозначно визначають її положення. Кожному моменту часу
однозначно визначають її положення. Кожному моменту часу  (2.2)
(2.2)
 . Наприклад, розв’язуючи останнє рівняння системи (2.2) відносно
. Наприклад, розв’язуючи останнє рівняння системи (2.2) відносно 
 (2.3)
(2.3) і
і  .
.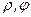 ); у просторі – циліндричною (
); у просторі – циліндричною ( ) або сферичною (
) або сферичною ( ) та іншими криволінійними системами координат. Закон руху точки в цих системах координат визначається аналогічно. Наприклад, у полярній системі координат рівняння руху точки мають вигляд
) та іншими криволінійними системами координат. Закон руху точки в цих системах координат визначається аналогічно. Наприклад, у полярній системі координат рівняння руху точки мають вигляд . (2.4)
. (2.4) . (2.5)
. (2.5) . (2.6)
. (2.6) . (2.7)
. (2.7) Координатний спосіб визначення руху точки в просторі застосовують як у теоретичних дослідженнях, так і при розв’язуванні конкретних задач.
Координатний спосіб визначення руху точки в просторі застосовують як у теоретичних дослідженнях, так і при розв’язуванні конкретних задач. , тобто дуговою координатою точки. Кожному моменту часу
, тобто дуговою координатою точки. Кожному моменту часу  є функцією часу
є функцією часу . (2.8)
. (2.8) , що його проходить точка за проміжок часу
, що його проходить точка за проміжок часу  . Щоб визначити шлях
. Щоб визначити шлях  (
( ) так, щоб протягом кожного проміжку
) так, щоб протягом кожного проміжку  . Шлях
. Шлях 

 . (2.9)
. (2.9) (2.10)
(2.10)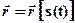 . (2.11)
. (2.11) траєкторії:
траєкторії: . (2.12)
. (2.12)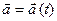 . Це поняття для векторної функції аналогічне поняттю графіка скалярної функції
. Це поняття для векторної функції аналогічне поняттю графіка скалярної функції  . Якщо
. Якщо  – неперервна функція, то неперервній зміні аргумента
– неперервна функція, то неперервній зміні аргумента  відповідає неперервна зміна функції
відповідає неперервна зміна функції  . Ця зміна визначається графіком.
. Ця зміна визначається графіком. Розглянемо векторну функцію
Розглянемо векторну функцію  , дістанемо відповідні значення функції
, дістанемо відповідні значення функції 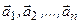 . Проведемо з фіксованої точки О вектори
. Проведемо з фіксованої точки О вектори  до
до  , то кінець вектора
, то кінець вектора  опише відрізок кривої, що називається годографом векторної функції. Отже,
опише відрізок кривої, що називається годографом векторної функції. Отже,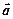 скалярного аргумента
скалярного аргумента  з початком у точці О і знайти проекції вектора
з початком у точці О і знайти проекції вектора  . (2.13)
. (2.13) .
. , (2.14)
, (2.14) є вектором, напрямленим по дотичній до годографа функції
є вектором, напрямленим по дотичній до годографа функції 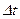 і відповідний йому приріст функції
і відповідний йому приріст функції  . Певному значенню функції
. Певному значенню функції  відповідає точка
відповідає точка  годографа. Відношення
годографа. Відношення  є вектором, нап-рямленим по січній
є вектором, нап-рямленим по січній  годографа функції
годографа функції  , а точка
, а точка  , то січна
, то січна 
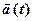 визначає зміну вектора
визначає зміну вектора 


