
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Випадок 1. Швидкість поступального руху і кутова швидкість обертання тіла ортогональні.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У точці Отже, При додаванні поступального і обертального рухів твердого тіла у випадку ортогональності швидкості поступального і кутової швидкості обертального рухів результуючим рухом тіла є миттєве обертання навколо осі, паралельної до даної, з тією ж кутовою швидкістю. Миттєва вісь обертання знаходиться від даної осі на відстані
Випадок 2. Швидкість поступального руху і кутова швидкість обертання тіла створюють довільний кут. Нехай тіло обертається з кутовою швидкістю
Рисунок 2.54 Нерухому систему координат Поступальний рух зі швидкістю
Вектор швидкості В точці Таким чином, результуючим рухом є сукупність обертального руху навколо осі Якщо швидкість
2.4.5. Метод “зупинки” (метод Вілліса)
Розглянемо прості передачі із зовнішнім (рис. 2.55) і внутрішнім (рис. 2.56) зачепленням коліс. Осі обертання коліс в обох випадках нерухомі. На підставі рівності швидкостей точок дотику коліс маємо:
у випадку зовнішнього зачеплення (рис. 2.55) і
у випадку зачеплення внутрішнього (рис. 2.56).
Рисунок 2.55
Знаки (+) і (-) у формулах (2.122) і (2.123) відповідають співнапрямленим і протилежно напрямленим кутовим швидкостям.
Рисунок 2.56
Розглянемо тепер епіциклічні або планетарні передачі теж з внутрішнім (рис. 2.57) і зовнішнім (рис. 2.58) зачепленням коліс. Ці передачі складаються з нерухомого колеса, кривошипа
Рисунок 2.57
Рисунок 2.58 Щоб дослідження епіциклічних передач звести до дослідження простих, подумки зупинимо водило (кривошип), тобто надамо всім ланкам механізму загального переносного обертального руху навколо осі На підставі (2.122) і (2.123) отримаємо для зовнішнього зачеплення (рис. 2.58)
для внутрішнього зачеплення (рис. 2.57)
Невідому кутову швидкість Для розв’язування задач зручно, користуючись методом “зупинки”, складати таблицю кутових швидкостей ланок механізму до і після зупинки. Далі розглянемо цей метод на конкретних прикладах.
Приклади
Приклад 2.9. На рис. 2.59 зображено механізм точильного станка, який використовують для отримання великих кутових швидкостей при малих обертах водила 4, що обертається навколо нерухомої осі
Рисунок 2.59 Розв’язання Надамо всім ланкам механізму кутової швидкості Складемо таблицю кутових швидкостей ланок механізму до і після “зупинки”
Колесо 2 і обойма 3 мають внутрішнє зачеплення, тому
де Колеса 1 і 2 знаходяться у зовнішньому зачепленні, отже,
Розв’язуючи сумісно рівняння, знаходимо
Отже, колесо 1 отримало кутову швидкість в 10 разів більшу за кутову швидкість водила. Напрям цього обертання збігається з напрямом обертання водила. Приклад 2.10. У зображеному на рис. 2.60 планетарному механізмі радіуси нерухомого зубчатого колеса 1 і рухомого колеса 3 однакові, радіус колеса 2 довільний. Довести, що колесо 3 здійснює поступальний рух.
Рисунок 2.60 Розв’язання Розв’яжемо цю задачу двома способами. Спосіб 1. Скористаємося теорією плоскопаралельного руху твердого тіла. Колеса 2 і 3 виконують плоскопаралельний рух. Побудуємо їх миттєві центри швидкостей і знайдемо кутові швидкості. Колесо 2 має миттєвий центр швидкостей в точці
і як такої, що належить колесу 2,
Порівнюючи ці два вирази, отримаємо:
Щоб знайти
Оскільки швидкості точок Спосіб 2. Скористаємося методом “зупинки”. Надамо всій системі переносного обертального руху з кутовою швидкістю (-
Перемноживши рівності, маємо
З отриманого результату можна зробити висновок: колесо 3 виконує поступальний рух, отже має місце пара обертань. Осі обертання паралельні і проходять через точки
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 686; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.68 (0.011 с.) |

 Припустимо, що тіло обертається з кутовою швидкістю
Припустимо, що тіло обертається з кутовою швидкістю  (відносний рух) навколо осі
(відносний рух) навколо осі  системи координат
системи координат 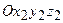 і разом з цією системою рухається поступально зі швидкістю
і разом з цією системою рухається поступально зі швидкістю  (переносний рух), при цьому
(переносний рух), при цьому  (рис. 2.53). Довільна точка
(рис. 2.53). Довільна точка  на осі обертання має швидкість
на осі обертання має швидкість  ), яка розташована в площині, перпендикулярній до вектора
), яка розташована в площині, перпендикулярній до вектора  .
. “зрівноважуються”, так як
“зрівноважуються”, так як  . Через точку
. Через точку  проходить миттєва вісь обертання, паралельна до осі
проходить миттєва вісь обертання, паралельна до осі  .
. , при цьому вектори
, при цьому вектори  (рис. 2.54).
(рис. 2.54).
 обираємо так, щоб вектори
обираємо так, щоб вектори 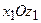 . На рис. 2.54 обидві системи координат збігаються.
. На рис. 2.54 обидві системи координат збігаються. :
: .
. розглянемо як момент пари обертань
розглянемо як момент пари обертань  . В результаті маємо в точці
. В результаті маємо в точці  і швидкість
і швидкість 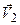 поступального руху.
поступального руху.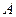 на відстані
на відстані 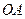 , що дорівнює плечу пари обертань (
, що дорівнює плечу пари обертань (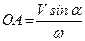 ), знаходиться миттєва вісь обертання
), знаходиться миттєва вісь обертання  . Вектор швидкості
. Вектор швидкості  ).
). , паралельної даній, з тією ж кутовою швидкістю і поступального руху вздовж цієї ж осі, тобто має місце гвинтовий рух. Цей рух називають також кінематичним гвинтом.
, паралельної даній, з тією ж кутовою швидкістю і поступального руху вздовж цієї ж осі, тобто має місце гвинтовий рух. Цей рух називають також кінематичним гвинтом. і кутова швидкість
і кутова швидкість 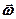 змінні, то рух тіла буде миттєво-гвинтовим рухом.
змінні, то рух тіла буде миттєво-гвинтовим рухом. (2.122)
(2.122)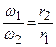 (2.123)
(2.123)

 (водила) і рухомого колеса (сателіта), яке є тілом, що виконує складний рух: обертається навколо двох паралельних осей: нерухомої О і рухомої А.
(водила) і рухомого колеса (сателіта), яке є тілом, що виконує складний рух: обертається навколо двох паралельних осей: нерухомої О і рухомої А.

 . Тоді передача перетвориться на просту, осі
. Тоді передача перетвориться на просту, осі 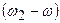 .
. ,
, .
. знаходимо з цих виразів.
знаходимо з цих виразів. 2 рад/с. Колесо 2, яке вільно насаджено на кінець
2 рад/с. Колесо 2, яке вільно насаджено на кінець  водила, котиться без ковзання по нерухомій обоймі 3 і передає обертання колесу 1, вільно насадженому на вісь
водила, котиться без ковзання по нерухомій обоймі 3 і передає обертання колесу 1, вільно насадженому на вісь  см,
см, 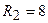 см.
см.
 , тобто “зупинимо” водило.
, тобто “зупинимо” водило.

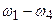



 .
. .
. ;
; 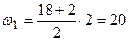 рад/с.
рад/с.

 .
.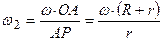 .
. побудуємо миттєвий центр швидкостей колеса 3. Для цього треба знайти швидкості двох його точок:
побудуємо миттєвий центр швидкостей колеса 3. Для цього треба знайти швидкості двох його точок: ;
; .
.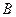 і
і 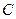 обчислені в довільний момент часу, і вони рівні, то колесо 3 виконує поступальний рух, і
обчислені в довільний момент часу, і вони рівні, то колесо 3 виконує поступальний рух, і  .
. ), тобто “зупинимо” кривошип
), тобто “зупинимо” кривошип 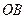 . Занесемо до таблиці значення кутових швидкостей до і після зупинки і, беручи до уваги, що всі колеса знаходяться у зовнішньому зачепленні, запишемо співвідношення між кутовими швидкостями:
. Занесемо до таблиці значення кутових швидкостей до і після зупинки і, беручи до уваги, що всі колеса знаходяться у зовнішньому зачепленні, запишемо співвідношення між кутовими швидкостями:


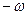


 ; 2-3:
; 2-3:  .
. .
.


