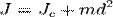Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поступальні та обертальні рухи твердого тіла. Кутова швидкість та кутове прискорення.Содержание книги
Поиск на нашем сайте
Тверде тіло — агрегатний стан речовини, що характеризується стабільністю форми на відміну від інших агрегатних станів рідини та газу. Поступальний рух — рух, при якому всі точки тіла або системи матеріальних точок переміщуються паралельними траєкторіями. Внаслідок поступального руху тіла усі його точки рухаються з однаковими швидкостями і прискореннями, тому для вивчення такого руху досить вивчити рух однієї точки, що належить даному тілу. Рух ізольованої матеріальної точки поступальний за означенням. Наприклад, рух поїзда по всьому шляху. Рух абсолютно твердого тіла можна подати у вигляді суми поступального руху й обертання. В загальному випадку довільної системи матеріальних точок рух можна подати у вигляді поступального руху і відносного руху точок системи одна щодо іншої. В класичній механіці поступальний рух задовільняє рівнянню: · де ·
Обертальний рух – це рух,при якому всі частинки твердого тіла переміщуються по колах, центри яких лежать на нерухомій площині, що називається віссю. При обертальному русі всі частини тіла переміщуються з різними лінійними швидкостями, але всі вони мають однакові кутові швидкість та прискорення, які є характеристиками обертального руху. Кутова́ шви́дкість — відношення зміни кута при обертанні до відрізку часу, за який ця зміна відбулася.
Вимірюється в радіанах за секунду. Оскільки зростання кута відраховується проти годинникової стрілки, то кутова швидкість додатня при обертанні проти годинникової стрілки і від'ємна при обертанні за годинниковою стрілкою. Якщо зміна кута нерівномірна, то вводиться миттєва кутова швидкість:
Кутове прискорення - похідна від кутової швидкості по часу.
де β- кутове прискорення, Кутове прискорення зване з тангенціальними прискоренням: аt=βr. Може бути ознакою різних видів обертальних рухів точки: 1)β=0 – рівномірний обертальний рух; 2)β=const – рівнозмінний обертальний рух. Момент інерції твердого тіла. Моменти інерції тіл найпростішої форми. Моме́нт іне́рції тіла відносно даної осі(одиниця виміру в системі СІ [кг*м2]) – склярна величина, яка дорівнює сумі добутків мас частинок на квадрати їхніх відстаней від осі ообертання.
J=∑m i r i 2, добуток m i r i 2 – момент інерції окремої частинки відносно осі обертання. Тобто момент інерції системи тіл відносно осі обертання дорівнює сумі моментів інерції складових частин системи відносно даної осі. Під моментом інерції розуміють міру інертності тіла при обертальному русі. Кожне тіло має конкретне значення моменту інерції відносно конкретної осі обертання. 1. Порожнистий товстостінний циліндр масою m та радіусами R1 та R2 відносно геометричної осі: J=(m*(R12+ R22))/2; порожнистий тонкостінний циліндр масою m та радіусом оболонки R відносно геометричної осі: J=mR2; суцільний циліндр масою m та радіусом оболонки R відносно геометричної осі: J=mR2/2; куля масою m та радіусом R, відносно осі, що проходить через центр кулі: J=2/5 mR2; стержень масою m і завдовжки l, відносно осі перпендикулярної до середини стержня: J=1/12 m l 2; той самий стержень відносно осі перпендикулярної до кінця стержня: J=1/3 m l 2. Теорема Гюйгенса-Штейнера Якщо відомий момент інерції тіла відносно осі, що проходить через центр його мас, то момент інерції відносно будь-якої іншої осі, що паралельна до даної визначається теоремою Штейнера (теоремою Гюйгенса-Штейнера): момент інерції тіла J відносно довільної осі дорівнює сумі моменту інерції цього тіла Jc відносно осі, що проходить через центр маси тіла паралельно до осі, що розглядається, і добутку маси тіла m на квадрат відстані d між осями:
Питання 31 Теорема Штейнера Теорема Гюйгенса-Штейнера Якщо відомий момент інерції тіла відносно осі, що проходить через центр його мас, то момент інерції відносно будь-якої іншої осі, що паралельна до даної визначається теоремою Штейнера (теоремою Гюйгенса-Штейнера): момент інерції тіла J відносно довільної осі дорівнює сумі моменту інерції цього тіла Jc відносно осі, що проходить через центр маси тіла паралельно до осі, що розглядається, і добутку маси тіла m на квадрат відстані d між осями:
Моментом інерції механічної системи відносно непорушної вісі а називається фізична величина І, яка дорівнює добутку мас матеріальних точок системи на квадрати їх відстані від вісі.
Іа=∑ri2mi Момент інерції тіла: Іа=∫r2dm=∫ r2pdV, де p-плотність тіла, dV – елементарний обсяг. Питання 32
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 435; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.115.172 (0.009 с.) |

 ,
,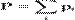 — сумарний імпульс усіх тіл механічної системи,
— сумарний імпульс усіх тіл механічної системи, - сумарна сила.
- сумарна сила.


 - кутова швидкість, t - час. Вимірюється в рад/c2.
- кутова швидкість, t - час. Вимірюється в рад/c2.