
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гравітаційна взаємодія поблизу поверхні Землі.Содержание книги
Поиск на нашем сайте
Гравітаційна взаємодія поблизу поверхні Землі.
оскільки γ, М і R — постійні величини. Таким чином, із закону всесвітнього тяжіння виходить, що поблизу Землі всі тіла падають з однаковим прискоренням g ≈ 9,8l м/сек2. Інакше кажучи, завдяки обертанню Землі навкруги своєї осі величина прискорення g не є постійною, а дещо змінюється залежно від широти і висоти місця. Приведене значення g відповідає широті 45° на рівні моря. Прискорення вільного падіння – це прискорення, якого набуває тіло під дією сили тяжіння і яке чисельно дорівнює силі, з якою гравітаційне поле Землі діє на тіло масою 1 кг. Електрична взаємодія. Закон Кулона. Закон Кулона — один з основних законів електростатики, який визначає величину та напрямок сили взаємодії між двома нерухомими точковими зарядами. Експериментально з задовільною точністю був вперше доведений Генрі Кавендішем у 1773, який використовував метод сферичного конденсатора, але його роботи не були опубліковані. В 1785 році закон був встановлений Шарлем Кулоном за допомогою спеціальних крутильних терезів.Електростатична сила взаємодії F12 двох точкових нерухомих зарядів q1 та q2 в вакуумі прямо пропорційна добутку абсолютних значень зарядів і обернено пропорційна квадрату відстані r12 між ними.
у векторній формі:
Сила взаємодії направлена вздовж прямої, що з'єднує заряди, причому однойменні заряди відштовхуються, а різнойменні притягуються. Сили, що визначаються законом Кулона адитивні. Коефіціент пропорційності k має назву електростатичної сталої та залежить від вибору одиниць виміру. Так в Міжнародній системі одиниць СІ k =1/(4πε0) ≈ 8,987742438 -987742438 ·109 Н·м2·Кл-2, де
1. Точковість зарядів— відстань між зарядженими тілами має бути набагато більшою від розмірів тіл. 2. Нерухомість зарядів. В протилежному випадку потрібно враховувати магнітне поле заряду, що рухається. В однорідному ізотропному середовищі сила взаємодії між зарядами зменшується в ε разів:
де ε діелектрична проникність середовища. Два роди зарядів Наелектризовані тертям шматочок янтарю і шматочок скла притягаються один до одного, але шматочки янтарю один від одного відштовхуються, шматочки скла — теж. Підкреслюючи відмінність у наелектризованості янтарю і скла, спочатку умовно говорили про «смоляну» і «скляну» електрику, а потім янтар назвали зарядженим негативно, а скло — позитивно. Тіло, на яке діють сили рухається з прискоренням, величина і напрям якого визначаються відношенням рівнодійної всіх сил до маси тіла. Математично це формулювання може бути записано так:
Або
Якщо m — константа. Третій закон Ньютона Взаємодія між матеріальними точками (тілами) визначається третім законом Ньютона: два тіла взаємодіють із силами рівними за величиною і напрямленими у протилежні боки вздовж прямої, яка з’єднує ці тіла. Тобто
де Наприклад, з якою силою тіло притягається до Землі, з такою ж силою воно діє на Землю (рис.1.9). Але, оскільки маси тіла та Землі розрізняються у багато разів, то й прискорення ці сили викликають різні згідно із другим законом Ньютона. Тіло падає з прискоренням вільного падіння
Треба пам’ятати, що сила дії та сила протидії хоч і однакові за величиною, але прикладені до різних тіл. Закон Гука Пружність — це здатність деформованих тіл відновлювати початкові форму і об’єм за умови припинення зовнішньої дії. Закон Гука встановлює лінійну залежність між деформацією й механічними напруженнями. Закон Гука справедливий для малих пружних деформацій. Модуль сили Гука: F упр = k | x |
Модуль Юнга Модуль Юнга — це характеристика пружніх властивостей ізотропних матеріалів, один із модулів пружності.
Модуль Юнга встановлює зв'язок між деформацією розтягу й механічним напруженням направленим на розтяг. Енергія деформованої пружини. Енергія — це фізична величина, що показує, яку роботу може виконати тіло. Енергія позначається літерою Е. У Системі Інтернаціональній енергія вимірюється в джоулях (Дж). Чим більшу роботу може виконати тіло, тим більшу енергію воно має. При виконанні роботи енергія тіла змінюється. Деформована пружина має запас потенціальної енергія пружної деформації. Для того, щоб деформувати пружину, необхідно виконати роботу. Ця робота дорівнює добутку сили на зміщення кінця Тоді робота, яку потрібно виконати для деформації пружини для зміщення на
Потенціальна енергія пружно деформованого тіла вимірюється тією роботою, яку тіло може здійснити. Отже,
Потенціальна енергія пружно деформованої пружини дорівнює половині добутку коефіцієнта жорсткості пружини на квадрат зміщення точки прикладення сили. 25. Робо́та - фізична величина, яка визначає енергетичні затрати при переміщенні фізичного тіла, чи його деформації. Робота зазвичай позначається латинською літерою A), в англомовній літературі - W (від англ. Work), й має розмірність енергії. У системі СІ робота вимірюється в Джоулях.
Потенціа́льна ене́ргія — частина енергії фізичної системи, що виникає завдяки взаємодії між тілами, які складають систему, та із зовнішніми щодо цієї системи тілами, й зумовлена розташуванням тіл у просторі. Разом із кінетичною енергією, яка враховує не тільки положення тіл у просторі, а й рух, потенціальна енергія складає механічну енергію фізичної сиcтеми. Потенціальна енергія матеріальної точки визначається як робота з її переміщення із точки простору, для якої визначається потенціальна енергія у якусь задану точку, потенціальна енергія якої приймається за нуль. Потенціальна енергія визначається лише для поля консервативних сил.
2.Через те, що механічна елементарна робота дорівнює:
та з, іншого боку, робота консервативних сил при елементарній зміні конфігурації системи дорівнює приросту потенціальної енергії, взятому зі знаком мінус, то робота здійснюється за рахунок зменшення потенціальної енергії:
тоді:
Звідси:
де Закон збереження енергії. Ене́ргія — загальна кількісна міра руху і взаємодії всіх видів матерії. Енергія не виникає ні з чого і нікуди не зникає, вона може тільки переходити з одного вигляду в інший (закон збереження енергії). Поняття енергії зв`язує всі явища природи в одне ціле, є загальною характеристикою стану фізичних тіл і фізичних полів. В системі СІ енергія вимірюється в джоулях(Дж). Поняття енергії зв'язане зі здатністю тіла або системи виконати роботу. При цьому тіло або система частково втрачає енергію, витрачаючи її на зміни в навколишніх тілах.
Закон збереження енергії - закон, який стверджує, що повна енергія в ізольованих системах не змінюється з часом. Проте енергія може перетворюватися з одного виду в інший. У термодинаміці закон збереження енергії відомий також під назвою першого закону термодинаміки. Закон збереження механічної енергії. У механіці закон збереження енергії стверджує, що в замкненій системі частинок, повна енергія, що є сумою кінетичної і потенціальної енергії не залежить від часу, тобто є інтегралом руху. Закон збереження енергії справедливий тільки для замкнених систем, тобто за умови відсутності зовнішніх полів чи взаємодій. Сили взаємодії між тілами, для яких виконується закон збереження механічної енергії називаються консервативними силами. Закон збереження механічної енергії не виконується для сил тертя, оскільки за наявності сил тертя відбувається перетворення механічної енергії в теплову. Закон збереження енергії в термодинаміці. У термодинаміці закон збереження енергії встановлює співвідношення між внутрішньою енергією тіла, кількістю теплоти, переданою тілу і виконаною роботою. Термодинаміка вивчає здебільшого нерухомі тіла, кінетична і потенціальна енергія яких залишається незмінною. Однак, ці тіла можуть виконувати роботу над іншими тілами, якщо, наприклад, змінювати їхню температуру. Отже, оскільки нагріте тіло може виконувати роботу, воно має певну енергію. Ця енергія отримала назву внутрішньої енергії. З точки зору фізики мікросвіту - фізики атомів і молекул, внутрішня енергія тіла є сумою кінетичних і потенціальних енергії частинок, з яких це тіло складається. Однак, з огляду на велику кількість та малі розміри частинок і загалом невідомі закони їхньої взаємодії, внутрішню енергію тіла визначити важко, виходячи з його будови. Проте очевидно, що вона залежить від температури тіла. Визначальним моментом для встановлення закону збереження енергії стало встановлення еквівалентності між теплом, кількісною характеристикою якого є кількість теплоти, і механічною роботою. Якщо тілу надати певну кількість теплоти Q, то частина її піде на виконання механічної роботи A, а частина на збільшення внутрішньої енергії тіла:
Ця формула складає основу першого закону термодинаміки. Аналогічним чином при виконанні механічної роботи, частина енергії втрачається у вигляді тепла, тобто йде на підвищення температури тіла й навколишнього середовища. Загалом сумарний притік енергії в систему мусить дорівнювати сумарному відтоку енергії з системи, плюс зміна енергії тіл, з яких складається сама система. Іншими словами, енергія може бути перетворена з одної форми в іншу, але не може бути створена чи знищена. Закон збереження енергії виключає можливість створення вічного двигуна першого роду. Перетворення енергії. Енергія одного виду може перетворюватися в енергію іншого виду, наприклад, хімічна енергія може перетворюватися в теплову, а теплова енергія в механічну тощо. В молекулі хімічної сполуки атоми зв'язані між собою хімічними зв'язками. Для того, щоб розірвати хімічний зв'язок потрібно затратити певну енергію, значення якої визначається типом зв'язку. В одних молекулах енергія зв'язку більша, в інших менша. Так, енергія зв'язку в молекулі вуглекислого газу СО2 більша, ніж сумарна енергія атома карбону у вугіллі й атомів оксигену в молекулі кисню O2. Тому можлива хімічна реакція горіння, внаслідок якої утворюється вуглекислий газ, а залишки хімічної енергії передаються поступальному, тепловому руху молекул, тобто перетворюються в тепло. Виділене внаслідок горіння тепло можна використати, наприклад, для нагріву пари в паровій турбіні, яка, обертаючись, створює електрорушійну силу в генераторі, продукуючи електроенергію. Електроенергія може, в свою чергу використовуватися для виконання механічної роботи, наприклад, підйому ліфта, або ж для освітлення, де електрична енергія перетворюється в енергію електромагнітних хвиль – світла. Теорема Гюйгенса-Штейнера Якщо відомий момент інерції тіла відносно осі, що проходить через центр його мас, то момент інерції відносно будь-якої іншої осі, що паралельна до даної визначається теоремою Штейнера (теоремою Гюйгенса-Штейнера): момент інерції тіла J відносно довільної осі дорівнює сумі моменту інерції цього тіла Jc відносно осі, що проходить через центр маси тіла паралельно до осі, що розглядається, і добутку маси тіла m на квадрат відстані d між осями:
Питання 31 Теорема Штейнера Теорема Гюйгенса-Штейнера Якщо відомий момент інерції тіла відносно осі, що проходить через центр його мас, то момент інерції відносно будь-якої іншої осі, що паралельна до даної визначається теоремою Штейнера (теоремою Гюйгенса-Штейнера): момент інерції тіла J відносно довільної осі дорівнює сумі моменту інерції цього тіла Jc відносно осі, що проходить через центр маси тіла паралельно до осі, що розглядається, і добутку маси тіла m на квадрат відстані d між осями:
Моментом інерції механічної системи відносно непорушної вісі а називається фізична величина І, яка дорівнює добутку мас матеріальних точок системи на квадрати їх відстані від вісі.
Іа=∑ri2mi Момент інерції тіла: Іа=∫r2dm=∫ r2pdV, де p-плотність тіла, dV – елементарний обсяг. Питання 32 Питання 33 Момент сили. Плече сили Для характеристики механічної дії на тіло, яке приводить до зміни обертального руху тіла, вводять поняття моменту сили. Моментом сили F відносно точки О називається векторна величина М, яка дорівнює векторному добутку радіус-вектора r, проведеного з точки О в точку прикладання сили на вектор сили F: М=r*F, [M]=H*м. Напрям моменту сили визначається правилом гвинта при повороті його від r до F. Момент сили - це вектор перпендикулярний, як до радіус-вектора точки, так і до сили, яка на цю точку діє. За абсолютною величиною момент сили дорівнює добутку сили на плече або
Найкоротшу відстань від точки опори до прямої, вздовж якої діє сила, називають плечем сили. Плече сили позначається літерою l та вимірюється в метрах. Для того щоб знайти плече сили, треба з точки опори опустити перпендикуляр на лінію дії сили. Питання 34 Правило важелів Архімеда У книжці «Про рівновагу і визначення центра ваги плоских фігур» Архімед уперше доводить відоме правило важеля: нерівні тягарі перебувають у рівновазі на важелі, якщо відстані центрів тягарів від точки опори важеля обернено пропорційні їх вагам. У цій самій праці Архімед визначає центри ваги прямокутників, паралелограмів, трикутників і т. д.Є всі підстави припускати, що тут він установив саме поняття центра ваги, а не поняття центра ваги тіла: це така точка, в якій досить підтримати тіло, щоб воно було в рівновазі у будь-якому положенні. Питання 35Гідростатика. Фізичні властивості рідиниГідроста́тика – розділ гідромеханіки, що вивчає закони рівноваги рідини, які знаходиться у стані абсолютного чи відносного спокою та рівноваги тіл, занурених у рідини за умови, коли відсутні переміщення часток рідини одна відносно одної. У механіці не враховується молекулярна будова середовища. На певний об’єм рідини діють внутрішні і зовнішні сили. Внутрішні сили зумовлені взаємодією частинок рідини, ці сили зрівноважуються. Зовнішні сили зумовлені дією сусідніх елементів, сили тяжіння тощо. У загальному випадку рідина зазнає дії масових і поверхневих сил. Обємні сили діют на елементарні об’єми, в яких знаходиться певна маса рідини: сили тяжіння, інерції. Поверхневі сили діють на поверхню, що обмежує елементарний об’єм. При дії поверхневих сил виникають деформації об’єму, які створюють пружні сили, дія яких однакова за значенням і протилежна за напрямом дії зовнішніх сил. Фізичні властивості рідини Всі рідини, коли рухаються, мають внутрішнє тертя, яке обумовлене в’язкими властивостями середовища. Нехтування в’язкими силами суттєво спрощує аналітичне дослідження. Замість реальної рідини виявляється доцільним розглядати модель ідеальної рідини. Ідеальна рідина – це абстрактна рідина без внутрішніх сил тертя. В’язкість нестисливої рідини з ростом температури зменшується. Крапельна рідина приймає форму посудини і утворює поверхню вільного рівня, яка відокремлює її від других рідин або газів з іншими фізичними властивостями. На такій поверхні особливо інтенсивно проявляється дія молекулярних сил зчеплення, що призводить до появи сил капілярності, змочуваності твердих поверхонь і до виникнення крапель і менісків. Густиною рідини r називається її маса, яка міститься в одиниці об’єму, ρ= m/V де m – маса рідини (кг) в об’ємі Питомою вагою однорідної рідини γ = G/V. (1.2) Між густиною і питомою вагою існує взаємозв’язок
Властивість рідин змінювати густину (питому вагу) при зміні температури широко використовується для створення природної циркуляції в котлах, опалювальних системах, для видалення продуктів спалювання тощо. В’язкість рідини. Всі реальні рідини мають певну в’язкість, яка проявляється у вигляді внутрішнього тертя при відносному переміщенні суміжних частинок рідини. В’язкість рідини – це її властивість чинити опір відносному зрушенню частинок. Одиницею в’язкості в системі СІ служить паскаль-секунда. Поверхневий натяг рідини, який зумовлений силами взаємодії молекул поверхневого шару рідини між собою намагається скоротити вільну поверхню рідини. Внаслідок цього рідина, що має криволінійну поверхню, зазнає додаткового зусилля, яке збільшує або зменшує тиск в рідині (Па). Звідси витікає закон Паскаля: тиск, що діє на рідину, передається рідиною однаково у всіх напрямках.Основне рівняння гідростатики показує, що абсолютний гідростатичний тиск в будь-якій точці простору, зайнятому рідиною, дорівнює сумі зовнішнього тиску p0 і надлишкового тиску ρgh:
З цього рівняння випливає рівність рівнів у сполучених посудинах, пояснення гідростатичного парадоксу та закон Архімеда. Закон Паскаля. Для рідин і газів, які перебувають в рівновазі, виконується закон Паскаля: тиск у будь-якій точці рідини або газу, кі перебувають у спокої, однаковий в усіх напрямках і передається в усіх напрямках однаково. Закон Паскаля лежить в основі закону сполучених посудин. Закон сполучених посудин: 1. Будь-яка рідина встановлюється у сполучених досить широких (некапілярних) посудинах на одному рівні незалежно від їх числа, розмірів та нахилу до горизонту.
Закон Паскаля лежить в основі роботи гідравлічних пресів, гідравлічних і пневматичних гальм в автомобілі. Закон Архімеда У зв’язку з тим, що на різних рівнях у рідині або газі тиски різні, на занурене в рідину або газ тіло діє виштовхувальна сила. Зако́н Архіме́да — основний закон гідростатики, згідно з яким на будь-яке тіло, занурене в рідину або газ, діє виштовхувальна сила, яка дорівнює вазі витисненої даним тілом рідини (газу) і за напрямом протилежна їй. Ця сила напрямлена вгору і прикладена до центру мас витісненого об’єму рідини. Цей центр назив. центром плавучості тіла. зміна тиску, зумовленого силою тяжіння з висотою зникає, а з нею зникає і виштовхувальна сила. Якщо сила тяжіння тіла G більша виштовхувальної (Архімедової) сили Р, тобто G > P, то тіло тоне. Якщо G = P, то тіло знаходиться в спокої на тій глибині, на яку воно занурено. Якщо G< P, то тіло спливає, причому спливання припиниться тоді, коли виштовхувальна сила дорівнюватиме силі тяжіння тіла. Сила тяжіння рідини в об'ємі рівному об’єму зануреної в неї частини тіла називається водовантажністю, а центр ваги цього об'єму – центром водовантажності. Формула ваги витісненої рідини
де g – прискорення вільного падіння, ρ - густина рідини, V - витіснений об'єм. Закон Архімеда використовується для оцінки плавучості та стійкої рівноваги кораблів. Закон Паскаля. Тиском p називають скалярну фізичну величину, що дорівнює відношенню модуля сили тиску, що діє перпендикулярно до поверхні, до площі цієї поверхні S:
У разі рівномірного розподілу сил тиску тиск на всіх ділянках поверхні однаковий і чисельно дорівнює силі тиску, що діє на поверхню одиничної площі. У СІ за одиницю тиску взято тиск, викликаний силою 1 Н, дія якої рівномірно розподілена по перпендикулярній до неї поверхні площею 1 м2. Цю одиницю тиску називають "паскалем" (Па): 1 Па = 1 Н/м2. Тиск всередині рідини або газу вимірюють за допомогою манометрів різних типів. Французький фізик Блез Паскаль встановив закон, який описує тиск рідин або газів. Закон Паскаля: тиск, який діє на рідину або газ в стані теплової рівноваги передається в усіх напрямах однаково.
На рідину, як і на всі тіла на Землі, діє сила тяжіння. Тому кожний шар рідини, яка знаходиться в посудині, своєю вагою тисне на інші шари, і цей тиск, за законом Паскаля, передається в усіх напрямках. Тобто всередині рідини існує тиск і на одному й тому ж рівні він однаковий в усіх напрямках. З глибиною тиск рідини зростає. Так само тиск рідини залежить і від властивостей рідини, тобто від її густини. На основі гідростатичного закону Паскаля працюють різні гідравлічні пристрої: гальмівні системи, преси тощо. Закон Архімеда. Закон Архімеда - основний закон гідростатики, згідно з яким на будь-яке тіло, занурене в рідину або газ, діє виштовхувальна сила, яка дорівнює вазі витисненої даним тілом рідини (газу) і за напрямом протилежна їй і прикладена у центрі мас витісненого об'єму рідини. Згідно із законом Архімеда вага всякого тіла в повітрі менша за вагу його в пустоті на величину, рівну вазі витісненого повітря. Якщо сила тяжіння тіла G більша виштовхувальної (Архімедової) сили Р, тобто G > P, то тіло тоне. Якщо G = P, то тіло знаходиться в спокої на тій глибині, на яку воно занурено(плаває). Якщо G< P, то тіло спливає, причому спливання припиниться тоді, коли виштовхувальна сила дорівнюватиме силі тяжіння тіла. Сила тяжіння рідини в об'ємі рівному об’єму зануреної в неї частини тіла називається водовантажністю, а центр ваги цього об'єму – центром водовантажності. Формула сили Архімеда
де g - прискорення вільного падіння, Цей закон також допомагає пояснити поведінку тіла частково зануреного у рідину (плаваюче тіло). Тіло частково занурене у рідину має центр ваги (SC) і центр плавучості (SW). При зміні кута нахилу центр плавучості переміщається, і тіло може повернутися у вихідне положення (стабільний стан) або відхилятись повністю (нестійкий стан). Метацентр — точка перетину осі плавання і вертикальної лінії дії виштовхуючої сили. Вісь плавання — вісь нормальна до площини плавання і проходить через центр тяжіння судна у вихідному його положенні. При невеликих відхиленнях кута положення тіла розміщення метецентру не залежить від кута. Якщо метацентр знаходиться вище від центру ваги тіла під впливом пари сил, то це заставляє тіло повернутися до вихідного стану. Якщо ж метацентр буде знаходитись нижче за центр ваги тіла, тіло продовжить відхилятись від стану рівноваги, іншими словами втратить стійкість. Відрізок від метацентру до центру ваги називається метацентричною висотою. Такі розрахунки проводяться, наприклад, при проектуванні суден. Рівняння Клапейрона Рівняння Клапейрона- Мендєлєєва – це рівняння стану ідеального газу для його довільної маси. Воно звучить так: при сталій кількості речовини ідеального газу добуток його тиску на об’єм прямо пропорційний абсолютній температурі.
Це рівняння було виведене Клапейроном. В – питома газова стала, яка залежить від роду газу і його кількості. Мендєлєєв надав рівнянню більш зручного для користування вигляду, скориставшись законом Авогадро. Завдяки цьому стала в рівнянні газового стану, розрахована на 1 моль речовини, буде дорівнювати: R=8,31 Дж/моль*К – універсальна газова стала. Звідси рівняння стану, розрахованого на 1 моль газу: pV=RT – рівняння Клапейрона-Мендєлєєва. Для будь-якої маси m газу рівняння Клапейрона-Мендєлєєва записується так:
Де μ – маса, яку має моль газу.
Ізотермічний процес. Якщо в рівнянні вважати Т - const, права частина рівняння буде величиною сталою: pV= const. Закон Бойля—Маріотта, або рівняння стану ідеального газу при ізотермічному процесі, означає: добуток тиску даної маси газу на об'єм, що його займає газ за сталої температури, є величиною сталою Графічно залежність між тиском і об'ємом газу за сталої температури зображають гіперболою. Ці криві називають ізотермами (кривими однакових температур). Чим вища температура, за якої відбувається процес, тим вище розташована ізотерма (Т1 <Т2< Т3).
тобто за незмінної маси газу і сталого тиску об'єм газу прямо пропорційний абсолютній температурі. Перехід газу з одного стану в інший за сталого тиску називають ізобарним процесом. Графічно такий процес в координатних осях V, Т зображується прямою, продовження якої проходить через початок координат,— ізобарою. Кут її нахилу а до осі температур залежить від тиску газу: чим більший тиск, тим менший кут нахилу Ізохорний процес. Розглянемо випадок, коли об'єм V газу залишається сталим. З рівняння Клапейрона випливає, що за цих умов сталим буде відношення тиску газу до його температури:
тобто за сталого об'єму тиск газу прямо пропорційний його абсолютній температурі Перехід газу з одного стану в інший за сталого об'єму називають ізохорним процесом. Графік цього процесу в координатах р, Т — пряма лінія, продовження якої проходить через початок координат; її називають ізохорою. Кут нахилу а ізохори до осі температур тим більший, чим менший об'єм газу.
α = 0,003661 К-1 53. закон Шарля. Ізохорний процес відбувається при сталому об’ємі газу (V=const). при V=const р/ V=const.- це рівняння називається рівнянням ізохорного процесу. Рівняння ізохорного процесу записують у вигляді р=р0(1+βt), де p0 і p –т иски при 0˚С і t˚C; β – термічний коефіцієнт тиску (β=0,003661). Рівняння показує, що в ізохоричному процесі тиск газу перебуває в лінійній залежності від температури. Температуру, при якій тиск газу дорівнює нулю, називають абсолютним нулем. Закон Дюлонга та Пті. Зако́н Дюлонга — Пті визначає питому теплоємність твердого тіла за формулою
Закон Дюлонга—Пті справедливий при температурах вищих за температуру Дебая. Питома теплоємність – характеристика речовини, яка вказує кількість теплоти, необхідної для нагрівання одиниці маси речовини на 1градус C, або ж кількість теплоти, що виділяється при охолодженні одиниці маси речовини. Відкритий закон був у 1819році. Фізична природа Для того, щоб підвищити температуру потрібно збільшити кінетичну енергію руху кожного із атомів твердого тіла. Однак, внаслідок сильної взаємодії атомів між собою, збільшення кінетичної енергії потребує рівного за величиною збільшення потенціальної енергії. Тому теплоємність твердого тіла вдвічі більша за теплоємність ідеального газу. Закон Дюлонга—Пті можна переписати для теплоємності твердого тіла у вигляді:
де С — теплоємність, Теплоємність – це фізична величина, яка визначається кількістю теплоти, яку потрібно надати тілу для підвищення його температури на один градус. Для справедливості закону Дюлонга-Пті необхідно, щоб енергії теплового руху вистачало для збудження всіх можливих типів коливань у твердому тілі. При низьких температурах деякі з коливань не збуджуються. Це явище зумовлене законами квантової статистики (в даному випадку — статистики Бозе-Ейнштейна). Тому при низьких температурах закон Дюлонга-Пті не діє. Як було встановлено П.Л. Дюлонгом і А.Г. Пті, молярна теплоємкість твердих одноатомних тіл майже однакова і дорівнює:
де R= 8,31 Закон Дюлонга і Пті є дійсним для твердих одноатомних тіл для достатньо високих температур. Для більшості тіл такою високою температурою є вже кімнатна температура. Для деяких тіл з малою атомною масою, наприклад, берилію, бора, вуглецю (структури алмазу), молярну теплоємкість можна визначити і при високих температурах за законом Дюлонга і Пті. Навпаки, при охолоджені, для всіх тіл закон Дюлонга і Пті не дає точне визначення молярної теплоємкості, тобто, є відходження від закону. Барометрична формула Барометри́чна фо́рмула— формула, за якою визначають залежність тиску або густини газу від висоти. Ця залежність зумовлена дією поля тяжіння Землі і тепловим рухом молекул газу (повітря). Припускаючи, що газ є ідеальним газом сталої температури, і вважаючи поле тяжіння Землі однорідним, отримують барометричну формулу такого вигляду:
де p0 — тиск на нульовому рівні (на рівні вибою в газових свердловинах, біля поверхні Землі або на рівні моря), Па; p — тиск на висоті h, м над цією поверхнею, Па; m — маса молекули (для повітря дорівнює масі молекули азоту), кг; g — прискорення вільного падіння, м/с2; k — стала Больцмана, Дж/К; T — абсолютна температура повітря, К. Барометрична формула є наближеною: при виведенні її не враховано залежності g i T від висоти, відхилення газу від ідеального газу тощо. Нею можна користуватися для визначення атмосферного тиску до висоти 11 км (з поправками на зміну температури). За уточненою барометричною формулою градуюють альтиметри, висотоміри. Зміну тиску нерухомого стовпа газу у свердловині розраховують за уточненою барометричною формулою Лапласа-Бабіне:
де p(z) — тиск газу на глибині z, м, Па; p0 — тиск газу на гирлі свердловини, Па; Γ — відносна густина газу (до повітря); Tс — середня температура газу, К; zΓ — середній коефіцієнт стисливості газу при середньому тиску і середній температурі газу. Барометричну формулу з певним обмеженням можна використати для визначення розподілу кількості колоїдних частинок по висоті рідинної або газової дисперсної системи, на які діє поле тяжіння. Барометрична формула є окремим випадком розподілу Больцмана.
Теорема Гауса Теорема Гауса пов’язує потік вектора напруженості електростатичного поля крізь довільну замкнену поверхню із зарядом, який охоплюється цією поверхнею. Теорема Гаусса формулюється так: потік вектора напруженості електростатичного поля у вакуумі ФЕ через замкнуту поверхню S зсередини назовні дорівнює алгебраїчній сумі зарядів, укладених усередині цієї поверхні, поділеній на електричну постійну ξ0. Теорема Гаусса:
Отриманий результат не
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.20.34 (0.019 с.) |

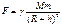 Гравіта́ція — це властивість масивних тіл притягуватись одне до одного. Гравітація є, зокрема, причиною земного тяжіння, внаслідок якого предмети падають додолу. Також орбіта Місяця навколо Землі і Землі та інших планет навколо Сонця визначається законами гравітації. Повертаючись до закону всесвітнього тяжіння і застосовуючи його до випадку взаємодії земної кулі з тілами, розташованими поблизу земної поверхні, одержимо:
Гравіта́ція — це властивість масивних тіл притягуватись одне до одного. Гравітація є, зокрема, причиною земного тяжіння, внаслідок якого предмети падають додолу. Також орбіта Місяця навколо Землі і Землі та інших планет навколо Сонця визначається законами гравітації. Повертаючись до закону всесвітнього тяжіння і застосовуючи його до випадку взаємодії земної кулі з тілами, розташованими поблизу земної поверхні, одержимо: де М — маса Землі, R — її радіус, т — маса тіла, h — його висота над земною поверхнею. Оскільки R»h, той вираз сили тяжіння тіл до Землі можна представити у вигляді:
де М — маса Землі, R — її радіус, т — маса тіла, h — його висота над земною поверхнею. Оскільки R»h, той вираз сили тяжіння тіл до Землі можна представити у вигляді:
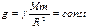 З іншого боку де g — прискорення вільного падіння тіл поблизу земної поверхні. З формул (7) і (8) слідує, що
З іншого боку де g — прискорення вільного падіння тіл поблизу земної поверхні. З формул (7) і (8) слідує, що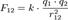
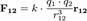
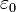 - електрична стала. В системі СГСГ одиниця вимірювання заряду обрана таким чином, що k =1. Наступні умови є необхідними для виконання сформульованого закону:
- електрична стала. В системі СГСГ одиниця вимірювання заряду обрана таким чином, що k =1. Наступні умови є необхідними для виконання сформульованого закону: ,
,
 ,
, ,
, – сила, яка діє на перше тіло з боку другого,
– сила, яка діє на перше тіло з боку другого,  – сила, яка діє на друге тіло з боку першого.
– сила, яка діє на друге тіло з боку першого. , а Земля не рухається.
, а Земля не рухається.
 пружини.
пружини. , буде:
, буде:
 .
. .
.


 ,
, ,
, .
. ,
, є сталою інтегрування, тобто потенціальна енергія визначається завжди з точністю до деякого значення.
є сталою інтегрування, тобто потенціальна енергія визначається завжди з точністю до деякого значення. ,
,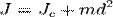

 .
.
 називається вага G одиниці об’єму цієї рідини
називається вага G одиниці об’єму цієї рідини
 .
.
 .
.
 ,
,

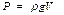
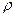 - густина рідини, V - витіснений об'єм.
- густина рідини, V - витіснений об'єм. або p2V2=BТ2.
або p2V2=BТ2.
 Якщо в газі відбуваються якісь процеси, то звичайно змінюються всі три його параметри: р, V і Т
Якщо в газі відбуваються якісь процеси, то звичайно змінюються всі три його параметри: р, V і Т Ізобарний процес. Нехай тепер газ знаходиться в умовах, коли сталим є його тиск р. З рівняння Клапейрона випливає, що в цьому випадку сталим буде відношення об'єму газу до його температури
Ізобарний процес. Нехай тепер газ знаходиться в умовах, коли сталим є його тиск р. З рівняння Клапейрона випливає, що в цьому випадку сталим буде відношення об'єму газу до його температури = const,
= const,
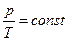
 52.Ізобарний процес відбувається в системі при сталому тиску (р=const). Такий процес можна здійснити, коли газ, наприклад, міститься в циліндрі з рухомим поршнем.зміна температури такого газу в такому циліндрі зумовлює переміщення поршня, тобто зміну об’єму. Тиск при цьому залишається сталим. При р=const V/T=const - ізобарного процесу (закон Гей-Люссака). Закон Гей-Люссака записують у вигляді V=V0(1+αt), де V0– об’єм газу при 0˚С; V- об’єм газу при температурі t˚C; α- коефіцієнт об’ємного розширення газу. Придосить низьких тисках величина α є однаковою для різних газів.
52.Ізобарний процес відбувається в системі при сталому тиску (р=const). Такий процес можна здійснити, коли газ, наприклад, міститься в циліндрі з рухомим поршнем.зміна температури такого газу в такому циліндрі зумовлює переміщення поршня, тобто зміну об’єму. Тиск при цьому залишається сталим. При р=const V/T=const - ізобарного процесу (закон Гей-Люссака). Закон Гей-Люссака записують у вигляді V=V0(1+αt), де V0– об’єм газу при 0˚С; V- об’єм газу при температурі t˚C; α- коефіцієнт об’ємного розширення газу. Придосить низьких тисках величина α є однаковою для різних газів.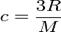 де c — питома теплоємність, R — універсальна газова стала, M — молярна маса.
де c — питома теплоємність, R — універсальна газова стала, M — молярна маса. ,
, — стала Больцмана, N — число атомів у кристалі.
— стала Больцмана, N — число атомів у кристалі.
 – універсальна газова стала.
– універсальна газова стала.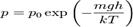 ,
, ,
,



