Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ждерело електричної взаємодії. Потенціал і напруженість поля точкового заряду.Содержание книги
Поиск на нашем сайте
Точковий заряд q створює в точці спостереження
Згідно з означенням електростатичного потенціалу
В середовищі потенціал зменшується в Напруженістю електричного поля називають фізичну векторну величину, що є силовою характеристикою електричного поля в кожній його точці і чисельно дорівнює відношенню сили, з якою поле діє на точковий заряд, поміщений у цю точку, до значення цього заряду. Напрям напруженості збігається з напрямом електричної сили, що діє на пробний позитивний заряд в цій точці:
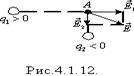
Вектор напруженості в будь-якій точці (А, В) електричного поля напрямлений вздовж прямої, що сполучає цю точку і заряд, від заряду, якщо q > 0, і до заряду, якщо q < 0 (рис. 4.1.6).
Із формул (4.1.5) і (4.1.6) знайдемо, що модуль напруженості електричного поля, створюваного точковим електричним зарядом,
Силові лінії електричного поля точкових зарядів незамкнені. Вони починаються на позитивних електричних зарядах і закінчуються на негативних (рис. 4.1.8 - 4.1.11). Віддалік від країв пластин силові лінії паралельні: електричне поле однакове у всіх точках.Завдяки принципу суперпозиції для знаходження напруженості поля системи заряджених частинок у будь-якій точці А досить знати вираз для напруженості поля точкового зарядженого тіла і додати вектори за правилом паралелограма:
Принцип суперпозиції (накладання) полів означає, що електричні поля під час накладання не впливають одне на одне. 9. Принцип суперпозиції для гравітаційного та кулонівського поля. Якщо E→1(r→) — поле системи зарядів №1, а E→2(r→) — поле системи зарядів №2, то при наявності зарядів обох систем: E→(r→) = E→1(r→) + E→2(r→).
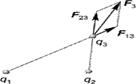
Найпростіша система складається з одного заряду. Отже, електричне поле системи зарядів дорівнює сумі полів, створюваних кожним зарядом окремо, під час відсутності інших зарядів: E→(r→) = ∑ j qj ∣r→ −r→j∣2 r→ −r→j ∣r→ −r→j∣. Тут qj,r→j — заряд і радіус-вектор j-го заряду. Правило додавання називають принципом суперпозиції, а формула є наслідком принципу суперпозиції і закону Кулона. Досліди показують, якщо на електричний заряд q діють одночасно електричні поля декількох зарядів, то результуюча сила дорівнює геометричній сумі сил, що діють з боку кожного поля окремо. Ця властивість електричних полів означає, що ці поля підлягають принципу суперпозиції: якщо в заданій точці простору різні заряджені частинки створюють електричні поля напруженістю Завдяки принципу суперпозиції для знаходження напруженості поля системи заряджених частинок у будь-якій точці А досить знати вираз для напруженості поля точкового зарядженого тіла і додати вектори за правилом паралелограма:
Принцип суперпозиції (накладання) полів означає, що електричні поля під час накладання не впливають одне на одне. Принцип суперпозиції дозволяє обчислити напруженість поля довільної системи зарядів, а не тільки точкових, зокрема і рівномірно зарядженої площини. За рівномірного розподілу електричного заряду q по поверхні площею S поверхнева густина заряду s є сталою і дорівнює:
У фізиці доведено, що напруженість електричного поля нескінченої площини з поверхневою густиною заряду s однакова в довільній точці простору і дорівнює:
де e0 - електрична стала.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.57.239 (0.009 с.) |

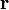 електричне поле з напруженістю
електричне поле з напруженістю
 .
. разів, де
разів, де 


 ,
, 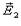
 і т.д., то результуюча напруженість поля в цій точці дорівнює геометричній сумі напруженостей полів частинок, тобто:
і т.д., то результуюча напруженість поля в цій точці дорівнює геометричній сумі напруженостей полів частинок, тобто: