
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння обертального руху твердого тілаСодержание книги
Поиск на нашем сайте
Обертальний рух – це рух,при якому всі частинки твердого тіла переміщуються по колах, центри яких лежать на нерухомій площині, що називається віссю. При обертальному русі всі частини тіла переміщуються з різними лінійними швидкостями, але всі вони мають однакові кутові швидкість та прискорення. Тверде тіло з нерухомою віссю обертання під дією сил, результуючий момент яких відносно осі не дорівнює нулю, приводитиметься в обертальний рух з певним кутовим прискоренням. Уявляючи тіло, як систему матеріальних точок, розглянемо одну з них – з масою m i, що лежить на відстані r i від осі обертання і перебуває під дією сили F i. Застосувавши до даної точки другий закон механіки: F i = m i *а і і замінивши тангенціальне прискорення на кутове F i = m i *r i *β. Оскільки в динаміці обертального руху істотну роль відіграє момент діючої сили, то введемо його помноживши вираз на плече r i: М i = m i *r i 2*β, де М i – момент сили F i відносно осі обертання. Записавши такі залежності для всіх матеріальних точок, на які поділено тіло, дістанемо: М=(∑m i *r i 2)*β – основне рівняння динаміки обертального руху. Остаточне рівняння динаміки обертального руху записують: М=Jβ. При сталому моменту інерції тіла кутове прискорення тіла прямо пропорційне результуючому моменту діючих сил. Якщо результуючий момент дорівнює нулю, то кутове прискорення також дорівнює нулю, тобто тіло перебуває в стані спокою або рівномірного обертального руху. Питання 33 Момент сили. Плече сили Для характеристики механічної дії на тіло, яке приводить до зміни обертального руху тіла, вводять поняття моменту сили. Моментом сили F відносно точки О називається векторна величина М, яка дорівнює векторному добутку радіус-вектора r, проведеного з точки О в точку прикладання сили на вектор сили F: М=r*F, [M]=H*м. Напрям моменту сили визначається правилом гвинта при повороті його від r до F. Момент сили - це вектор перпендикулярний, як до радіус-вектора точки, так і до сили, яка на цю точку діє. За абсолютною величиною момент сили дорівнює добутку сили на плече або
Найкоротшу відстань від точки опори до прямої, вздовж якої діє сила, називають плечем сили. Плече сили позначається літерою l та вимірюється в метрах. Для того щоб знайти плече сили, треба з точки опори опустити перпендикуляр на лінію дії сили.
Питання 34 Правило важелів Архімеда У книжці «Про рівновагу і визначення центра ваги плоских фігур» Архімед уперше доводить відоме правило важеля: нерівні тягарі перебувають у рівновазі на важелі, якщо відстані центрів тягарів від точки опори важеля обернено пропорційні їх вагам. У цій самій праці Архімед визначає центри ваги прямокутників, паралелограмів, трикутників і т. д.Є всі підстави припускати, що тут він установив саме поняття центра ваги, а не поняття центра ваги тіла: це така точка, в якій досить підтримати тіло, щоб воно було в рівновазі у будь-якому положенні. Питання 35Гідростатика. Фізичні властивості рідиниГідроста́тика – розділ гідромеханіки, що вивчає закони рівноваги рідини, які знаходиться у стані абсолютного чи відносного спокою та рівноваги тіл, занурених у рідини за умови, коли відсутні переміщення часток рідини одна відносно одної. У механіці не враховується молекулярна будова середовища. На певний об’єм рідини діють внутрішні і зовнішні сили. Внутрішні сили зумовлені взаємодією частинок рідини, ці сили зрівноважуються. Зовнішні сили зумовлені дією сусідніх елементів, сили тяжіння тощо. У загальному випадку рідина зазнає дії масових і поверхневих сил. Обємні сили діют на елементарні об’єми, в яких знаходиться певна маса рідини: сили тяжіння, інерції. Поверхневі сили діють на поверхню, що обмежує елементарний об’єм. При дії поверхневих сил виникають деформації об’єму, які створюють пружні сили, дія яких однакова за значенням і протилежна за напрямом дії зовнішніх сил. Фізичні властивості рідини Всі рідини, коли рухаються, мають внутрішнє тертя, яке обумовлене в’язкими властивостями середовища. Нехтування в’язкими силами суттєво спрощує аналітичне дослідження. Замість реальної рідини виявляється доцільним розглядати модель ідеальної рідини. Ідеальна рідина – це абстрактна рідина без внутрішніх сил тертя. В’язкість нестисливої рідини з ростом температури зменшується. Крапельна рідина приймає форму посудини і утворює поверхню вільного рівня, яка відокремлює її від других рідин або газів з іншими фізичними властивостями. На такій поверхні особливо інтенсивно проявляється дія молекулярних сил зчеплення, що призводить до появи сил капілярності, змочуваності твердих поверхонь і до виникнення крапель і менісків.
Густиною рідини r називається її маса, яка міститься в одиниці об’єму, ρ= m/V де m – маса рідини (кг) в об’ємі Питомою вагою однорідної рідини γ = G/V. (1.2) Між густиною і питомою вагою існує взаємозв’язок
Властивість рідин змінювати густину (питому вагу) при зміні температури широко використовується для створення природної циркуляції в котлах, опалювальних системах, для видалення продуктів спалювання тощо. В’язкість рідини. Всі реальні рідини мають певну в’язкість, яка проявляється у вигляді внутрішнього тертя при відносному переміщенні суміжних частинок рідини. В’язкість рідини – це її властивість чинити опір відносному зрушенню частинок. Одиницею в’язкості в системі СІ служить паскаль-секунда. Поверхневий натяг рідини, який зумовлений силами взаємодії молекул поверхневого шару рідини між собою намагається скоротити вільну поверхню рідини. Внаслідок цього рідина, що має криволінійну поверхню, зазнає додаткового зусилля, яке збільшує або зменшує тиск в рідині (Па). Звідси витікає закон Паскаля: тиск, що діє на рідину, передається рідиною однаково у всіх напрямках.Основне рівняння гідростатики показує, що абсолютний гідростатичний тиск в будь-якій точці простору, зайнятому рідиною, дорівнює сумі зовнішнього тиску p0 і надлишкового тиску ρgh:
З цього рівняння випливає рівність рівнів у сполучених посудинах, пояснення гідростатичного парадоксу та закон Архімеда. Закон Паскаля. Для рідин і газів, які перебувають в рівновазі, виконується закон Паскаля: тиск у будь-якій точці рідини або газу, кі перебувають у спокої, однаковий в усіх напрямках і передається в усіх напрямках однаково. Закон Паскаля лежить в основі закону сполучених посудин. Закон сполучених посудин: 1. Будь-яка рідина встановлюється у сполучених досить широких (некапілярних) посудинах на одному рівні незалежно від їх числа, розмірів та нахилу до горизонту.
Закон Паскаля лежить в основі роботи гідравлічних пресів, гідравлічних і пневматичних гальм в автомобілі. Закон Архімеда У зв’язку з тим, що на різних рівнях у рідині або газі тиски різні, на занурене в рідину або газ тіло діє виштовхувальна сила. Зако́н Архіме́да — основний закон гідростатики, згідно з яким на будь-яке тіло, занурене в рідину або газ, діє виштовхувальна сила, яка дорівнює вазі витисненої даним тілом рідини (газу) і за напрямом протилежна їй. Ця сила напрямлена вгору і прикладена до центру мас витісненого об’єму рідини. Цей центр назив. центром плавучості тіла. зміна тиску, зумовленого силою тяжіння з висотою зникає, а з нею зникає і виштовхувальна сила. Якщо сила тяжіння тіла G більша виштовхувальної (Архімедової) сили Р, тобто G > P, то тіло тоне. Якщо G = P, то тіло знаходиться в спокої на тій глибині, на яку воно занурено. Якщо G< P, то тіло спливає, причому спливання припиниться тоді, коли виштовхувальна сила дорівнюватиме силі тяжіння тіла. Сила тяжіння рідини в об'ємі рівному об’єму зануреної в неї частини тіла називається водовантажністю, а центр ваги цього об'єму – центром водовантажності.
Формула ваги витісненої рідини
де g – прискорення вільного падіння, ρ - густина рідини, V - витіснений об'єм. Закон Архімеда використовується для оцінки плавучості та стійкої рівноваги кораблів. Закон Паскаля. Тиском p називають скалярну фізичну величину, що дорівнює відношенню модуля сили тиску, що діє перпендикулярно до поверхні, до площі цієї поверхні S:
У разі рівномірного розподілу сил тиску тиск на всіх ділянках поверхні однаковий і чисельно дорівнює силі тиску, що діє на поверхню одиничної площі. У СІ за одиницю тиску взято тиск, викликаний силою 1 Н, дія якої рівномірно розподілена по перпендикулярній до неї поверхні площею 1 м2. Цю одиницю тиску називають "паскалем" (Па): 1 Па = 1 Н/м2. Тиск всередині рідини або газу вимірюють за допомогою манометрів різних типів. Французький фізик Блез Паскаль встановив закон, який описує тиск рідин або газів. Закон Паскаля: тиск, який діє на рідину або газ в стані теплової рівноваги передається в усіх напрямах однаково.
На рідину, як і на всі тіла на Землі, діє сила тяжіння. Тому кожний шар рідини, яка знаходиться в посудині, своєю вагою тисне на інші шари, і цей тиск, за законом Паскаля, передається в усіх напрямках. Тобто всередині рідини існує тиск і на одному й тому ж рівні він однаковий в усіх напрямках. З глибиною тиск рідини зростає. Так само тиск рідини залежить і від властивостей рідини, тобто від її густини. На основі гідростатичного закону Паскаля працюють різні гідравлічні пристрої: гальмівні системи, преси тощо. Закон Архімеда. Закон Архімеда - основний закон гідростатики, згідно з яким на будь-яке тіло, занурене в рідину або газ, діє виштовхувальна сила, яка дорівнює вазі витисненої даним тілом рідини (газу) і за напрямом протилежна їй і прикладена у центрі мас витісненого об'єму рідини. Згідно із законом Архімеда вага всякого тіла в повітрі менша за вагу його в пустоті на величину, рівну вазі витісненого повітря. Якщо сила тяжіння тіла G більша виштовхувальної (Архімедової) сили Р, тобто G > P, то тіло тоне. Якщо G = P, то тіло знаходиться в спокої на тій глибині, на яку воно занурено(плаває). Якщо G< P, то тіло спливає, причому спливання припиниться тоді, коли виштовхувальна сила дорівнюватиме силі тяжіння тіла. Сила тяжіння рідини в об'ємі рівному об’єму зануреної в неї частини тіла називається водовантажністю, а центр ваги цього об'єму – центром водовантажності.
Формула сили Архімеда
де g - прискорення вільного падіння, Цей закон також допомагає пояснити поведінку тіла частково зануреного у рідину (плаваюче тіло). Тіло частково занурене у рідину має центр ваги (SC) і центр плавучості (SW). При зміні кута нахилу центр плавучості переміщається, і тіло може повернутися у вихідне положення (стабільний стан) або відхилятись повністю (нестійкий стан). Метацентр — точка перетину осі плавання і вертикальної лінії дії виштовхуючої сили. Вісь плавання — вісь нормальна до площини плавання і проходить через центр тяжіння судна у вихідному його положенні. При невеликих відхиленнях кута положення тіла розміщення метецентру не залежить від кута. Якщо метацентр знаходиться вище від центру ваги тіла під впливом пари сил, то це заставляє тіло повернутися до вихідного стану. Якщо ж метацентр буде знаходитись нижче за центр ваги тіла, тіло продовжить відхилятись від стану рівноваги, іншими словами втратить стійкість. Відрізок від метацентру до центру ваги називається метацентричною висотою. Такі розрахунки проводяться, наприклад, при проектуванні суден.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.144.75 (0.012 с.) |

 .
.
 називається вага G одиниці об’єму цієї рідини
називається вага G одиниці об’єму цієї рідини
 .
.
 .
.
 ,
,

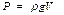
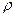 - густина рідини, V - витіснений об'єм.
- густина рідини, V - витіснений об'єм.


