
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Середньої швидкості та за середньою швидкістю вихідної ланкиСодержание книги
Поиск на нашем сайте
Кривошипно - коромисловий механізм. Задано довжину коромисла Коефіцієнт зміни середньої швидкості
Зазвичай величина коефіцієнта Отже,
З виразу (7.8) знаходимо кут
Після цього задача зводиться до знаходження центра обертання А кривошипа. Побудуємо кут ходу коромисла з вершиною у довільно вибраній точці D, а на його сторонах відкладемо довжину коромисла l
Рис. 7.4 Після цього довжини кривошипа та шатуна вираховуємо за формулами (7.5). Зазначимо, якщо в спроектованому механізмі максимальний кут тиску виявиться більшим за допустимий, слід вибрати інше положення центра обертання кривошипа (на колі радіуса r, вище за точку А). Кривошипно-повзунний механізм. У центральному кривошипно-повзунному механізмі швидкість повзуна в прямому та оберненому рухах однакова, коефіцієнт зміни середньої швидкості При синтезі таких механізмів часто виникає задача проектування за відомою середньою швидкістю
де З (7.9) одержуємо довжину кривошипа
Довжину шатуна визначаємо за вибраним коефіцієнтом Синтез кривошипно-повзунного механізму зі зміщенням за заданим коефіцієнтом зміни середньої швидкості
Розв’язавши рівняння (7.10) відносно кута
Після цього задача зводиться до знаходження центра обертання А кривошипа, яка є аналогічною до розглянутої задачі для кривошипно-коромислового механізму. Проводимо через середину хода h повзуна пряму, перпендикулярну до С2С1 (рис. 7.4, б). Далі, через точку С1 проводимо пряму, що складає кут Кулісний механізм. Розглянемо проектування цих механізмів на прикладі шестиланкового механізму з коливною кулісою (рис. 7.5). Для таких механізмів, як правило, відомо хід h вихідної ланки та коефіцієнт зміни її середньої швидкості Виявляється, що для механізмів даного виду коефіцієнт
Як і у попередніх задачах, де зустрічається коефіцієнт зміни середньої швидкості вихідної ланки, знаходимо кут
Для визначення довжини куліси розглянемо її крайнє ліве положення
а з прямокутного
Рис. 7.5 З іншого боку, при вертикальному положенні куліси можна записати таке співвідношення, що зв’язує розміри
де а – розмір, що вибирають з конструктивних міркувань. З виразу (7.12), після підстановки (7.11), знаходимо
Щодо кутів тиску, то при ведучому кривошипі кут З метою забезпечення найменшого кута тиску
де Довжина шатуна 4 виражається через заданий допустимий кут тиску з
Для інших кулісних механізмів синтез виконується подібним способом.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.47.139 (0.007 с.) |

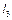 , два його крайніх положення за допомогою кутів
, два його крайніх положення за допомогою кутів 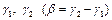 , а також коефіцієнт зміни середньої швидкості
, а також коефіцієнт зміни середньої швидкості 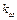 вихідної ланки 3. Потрібно знайти: довжини кривошипа
вихідної ланки 3. Потрібно знайти: довжини кривошипа 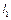 , шатуна
, шатуна 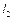 та стояка
та стояка  (рис.7.4, а).
(рис.7.4, а). . (7.7)
. (7.7) , а рух у протилежному напрямі – за марнохід – кривошип повернеться на кут
, а рух у протилежному напрямі – за марнохід – кривошип повернеться на кут  . Зазначимо, що більший з центральних кутів повороту кривошипа
. Зазначимо, що більший з центральних кутів повороту кривошипа 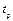 та марноходу
та марноходу  кривошип повернеться, відповідно, на кути
кривошип повернеться, відповідно, на кути  , де
, де 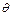 - кут перекриття, кут між положеннями шатуна, що відповідають крайнім положенням коромисла.
- кут перекриття, кут між положеннями шатуна, що відповідають крайнім положенням коромисла.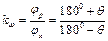 . (7.8)
. (7.8)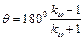 .
.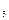 . Отримуємо точки С1, С2. Проводимо бісектрису ЕD кута
. Отримуємо точки С1, С2. Проводимо бісектрису ЕD кута  . На продовженні прямої ЕD зі сторони т. С2 відкладаємо кут перекриття
. На продовженні прямої ЕD зі сторони т. С2 відкладаємо кут перекриття 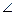 С1АС2=
С1АС2= 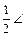 С1FC2=
С1FC2=  ). Відмітимо, що для більшої точності радіус r=C2F допоміжного кола можна порахувати за формулою
). Відмітимо, що для більшої точності радіус r=C2F допоміжного кола можна порахувати за формулою 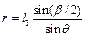 .
.
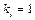 .
.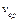 вихідної ланки. Для центрального механізму хід повзуна дорівнює подвоєній довжині кривошипа. Тому можна записати
вихідної ланки. Для центрального механізму хід повзуна дорівнює подвоєній довжині кривошипа. Тому можна записати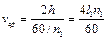 , (7.9)
, (7.9) , об/хв – частота обертання кривошипа.
, об/хв – частота обертання кривошипа. .
.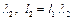 .
.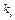 та ходом вихідної ланки. Коефіцієнт зміни середньої швидкості вихідної ланки для даного механізму
та ходом вихідної ланки. Коефіцієнт зміни середньої швидкості вихідної ланки для даного механізму . (7.10)
. (7.10) .
.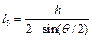 ,
,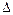 АВС визначаємо співвідношення між розмірами ланок
АВС визначаємо співвідношення між розмірами ланок 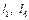
 (7.11)
(7.11)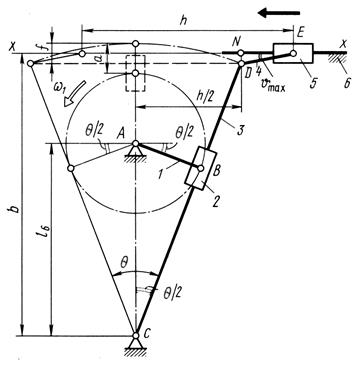
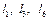
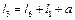 , (7.12)
, (7.12)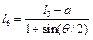 .
. =0, тобто за весь період руху напрям зусилля, що передається від кулісного каменя (повзун 2) до куліси 3, співпадає зі швидкістю точки прикладання зусилля. Даний факт є важливою позитивною властивістю цих механізмів.
=0, тобто за весь період руху напрям зусилля, що передається від кулісного каменя (повзун 2) до куліси 3, співпадає зі швидкістю точки прикладання зусилля. Даний факт є важливою позитивною властивістю цих механізмів.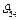 при передачі зусилля від шатуна 4 до веденого повзуна 5 його напрямну хх необхідно розмістити таким чином, щоб вона ділила стрілку сегмента f навпіл, тоді
при передачі зусилля від шатуна 4 до веденого повзуна 5 його напрямну хх необхідно розмістити таким чином, щоб вона ділила стрілку сегмента f навпіл, тоді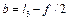 ,
,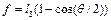 .
.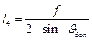 .
.


