Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рядове зачеплення з паразитними колесами. Рядове зачеплення з паразитними колесами характеризується тим, що на кожному з проміжних валів розміщено лише одне колесо.Содержание книги
Поиск на нашем сайте
Для здійснення передачі руху між валами, які розміщені на великій відстані або, якщо потрібно, щоб ведений вал обертався в тому ж самому напрямі, що й ведучий, на проміжних валах закріплюють по одному колесу, які не впливають на передатне відношення. Ці колеса називаються паразитними, а весь ряд – паразитним
Таким чином, число зубців паразитних коліс не впливає на абсолютну величину передатного відношення. Паразитні колеса впливають лише на його знак. Проміжні колеса застосовують для передачі обертання з одного валу на інший при великій міжосьовій відстані, а також для зміни напрямку обертання веденого валу. Число зубців проміжних коліс не впливає на абсолютну величину передатного відношення, але ці колеса витрачають на тертя певну потужність – тому проміжні колеса називаються паразитними. 9.13. Кінематичний аналіз диференціальних та планетарних механізмів
Зубчасті передачі з рухомими осями коліс. Епіциклічні передачі. У розглянутих зубчастих механізмах геометричні осі всіх коліс не змінюють свого положення у просторі. Можливі й такі зубчасті механізми, у яких геометричні осі одного чи кількох коліс переміщуються у просторі. До числа таких зубчастих механізмів відносять так звані диференціальні та планетарні механізми. Деколи їх називають епіциклічними механізмами. Епіциклічною передачею називають механізм, складений з зубчастих (фрикційних) коліс, одне або кілька з яких виконують складний обертальний рух, що складається з обертального руху навколо власної осі і разом з віссю – навколо зчепленого з ним зубчастого колеса (від слів “епіцикл” – коло, центр якого рівномірно рухається по іншому колу). Ці механізми можна поділити на планетарні механізми, що мають одну ступінь вільності і диференціальні механізми, що мають два й більше ступенів вільності. Схему найпростішого диференціального механізму наведено на рис. 9.25: колеса 1 і 3 називають центральними, їхні осі
Рис. 9.25
Колеса, які обертаються навколо центральної геометричної осі, називають центральними. Причому, колесо, що має зубці зовнішнього зачеплення, прийнято називати – сонячним, а колесо з зубцями внутрішнього зачеплення – коронним. Відмітимо, що у дійсного механізму є декілька симетрично розташованих сателітів. Їх встановлюють з метою зменшення габаритів механізму, зниження зусиль в зачепленні, розвантаження підшипників центральних коліс, покращення зрівноваження водила. Але у цьому випадку механізм має пасивні умови зв’язку ( Кінематичне дослідження епіциклічних механізмів виконують за допомогою методу інверсії (обернення руху, зупинки). Застосувавши метод інверсії руху, умовно перетворимо диференціальний механізм в обернений механізм, тобто у звичайний зубчастий механізм з нерухомими осями. Механізм, який дістали в результаті застосування методу обернення руху, називають оберненим. Ступінь рухомості диференціального механізму визначають за формулою П.Л. Чебишева.
Епіциклічна передача, у якої обидва центральні колеса рухомі і ступінь рухомості якої дорівнює двом, називають диференціальною. Отже, диференціальний механізм має два ступеня вільності, тобто для визначення руху всіх його ланок потрібно задати закон руху двом ланкам. Наприклад, задавши У диференціальному механізмі може відбуватися або розкладання руху (від одного ведучого на два ведених), або складання руху. Таким чином, за допомогою диференціальної передачі можна на одному валі здійснити рух, що передається йому від двох незалежних двигунів. Проведемо кінематичне дослідження диференціального зубчастого механізму аналітичним методом – виведемо формулу, що встановлює зв’язок між кутовими швидкостями ланок. Нехай кутові швидкості ланок диференціального механізму
Передатне відношення рядової зубчастої передачі можна знайти за формулою
де верхній індекс, буква або цифра у дужках – Це формула Вілліса, яка встановлює співвідношення між кутовими швидкостями ланок диференціального механізму. У цій формулі треба задати дві кутові швидкості, щоб визначити кутову швидкість третьої ланки. Оскільки відоме тільки передатне відношення Планетарні механізми. Закріпимо одне центральне колесо, наприклад 3 (рис. 9.25). Нерухоме центральне колесо називається опорним. У розглядуваному випадку ступінь рухомості епіциклічної передачі буде
Епіциклічна передача, ступінь рухомості якої дорівнює одиниці й одне із центральних коліс якої закріплене, називається планетарною передачею. Отже, кожний диференціальний механізм можливо перетворити у планетарний механізм, якщо закріпити одне з центральних коліс. І навпаки планетарний механізм, що має нерухоме колесо можливо перетворити у диференціал, якщо звільнити нерухоме (опорне) колесо і надати йому обертання. Це так звана властивість оберненості планетарних механізмів, яка дозволяє застосовувати однакові методи дослідження та проектування для планетарних і диференціальних редукторів. При цьому кожному елементарному диференціалу буде відповідати два планетарних механізми. Користуючись формулою Вілліса, визначимо зв’язок між кутовими швидкостями ланок планетарної передачі, тобто передатне відношення
звідки
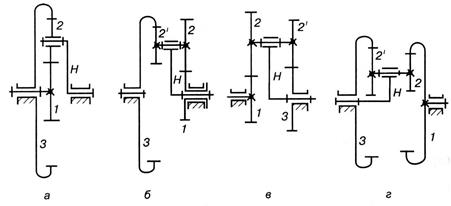
Отже, передатне відношення планетарного механізму дорівнює різниці між одиницею та передатним відношенням оберненого механізму. Ця формула справедлива для будь-якої схеми планетарного редуктора за наявності нерухомого центрального колеса. Передатне відношення Велике передатне відношення епіциклічних передач за малих їхніх габаритних розмірів порівняно з рядовим зачепленням, яке забезпечило б таке передатне відношення є суттєвою перевагою, що сприяла їх широкому розповсюдженню в металорізальних верстатах, літаках, транспортних машинах. Синтез планетарних механізмів. Розв’язання задачі синтезу планетарних механізмів можна поділити на два етапи: – вибір схеми планетарного механізму; – вибір числа зубців механізму. Вибір схеми планетарного механізму. В інженерній практиці отримали розповсюдження чотири схеми найпростіших планетарних механізмів, у яких сателіти зачіплюються одночасно з двома центральними колесами (рис. 9.26). Усі вони мають три основні вали, один з яких нерухомий. Почергове гальмування одного з валів дозволяє отримати у кожному механізмі на виході три різні швидкості. Передатне відношення усіх цих редукторів визначається за однією формулою. У загальному випадку вибір схеми можна виконати тільки детальним порівнянням різних варіантів. Підбір чисел зубців коліс планетарних механізмів треба виконувати, щоб задовольнялись умови співвісності, сусідства та складання. Спроектований механізм має бути компактним і забезпечувати задане передатне відношення. Умова співвісності полягає в тому, щоб геометричні осі ведучого та веденого валів збігалися. Умова сусідства полягає в тому, щоб кола виступів сателітів не торкалися і не перетиналися.
Рис. 9.26 Умова складання вимагає, щоб зуби кожного сателіта ввійшли в зачеплення з обома центральними колесами. Література
ЗМІСТ
Для заміток
ТЕОРІЯ МЕХАНІЗМІВ І МАШИН
Навчальний посібник
Ярошевич Микола Павлович
Комп’ютерний набір та верстка: Віктор Мартинюк Дизайн: Віктор Мартинюк Редактор: Лариса Тиха
Підписано до друку. Формат 60х84/16 Папір офс. Гарн. Таймс. Ум. друк.арк. 13,5 Обл.-вид.арк. 12,0. Наклад 50 прим. Зам. 4172
Редакційно-видавничий відділ Луцького національного технічного університету 43018 м. Луцьк, вул. Львівська, 75.
Ярошевич М.П.
Теорія механізмів І машин
Навчальний посібник
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.26.149 (0.011 с.) |

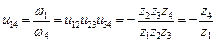 .
.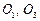 нерухомі. Колесо 2 з рухомою віссю
нерухомі. Колесо 2 з рухомою віссю  називають планетарним або сателітом (колесо 2 обертається навколо власної осі і разом з віссю – навколо колеса 1). Ланку, на якій розміщено осі сателітів, називають водилом Н (інколи позначають літерою S). Наголосимо, що водило є рухомою ланкою.
називають планетарним або сателітом (колесо 2 обертається навколо власної осі і разом з віссю – навколо колеса 1). Ланку, на якій розміщено осі сателітів, називають водилом Н (інколи позначають літерою S). Наголосимо, що водило є рухомою ланкою.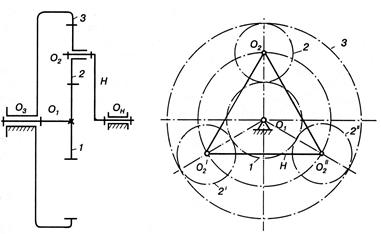
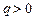 ), тобто він є статично невизначеним. При кінематичних розрахунках враховується лише один сателіт, оскільки інші є пасивними у кінематичному відношенні.
), тобто він є статично невизначеним. При кінематичних розрахунках враховується лише один сателіт, оскільки інші є пасивними у кінематичному відношенні.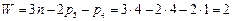 .
.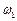 і
і  , матимемо визначений рух водила –
, матимемо визначений рух водила – 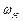 , або задавши
, або задавши 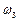 і
і 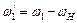 ;
; 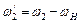 ;
;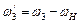 ;
; 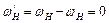 .
.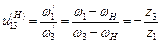 ,
, означає, що для наведеного випадку водило
означає, що для наведеного випадку водило 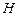 – нерухоме (умовно зупинене), тобто передатне відношення визначене за умови нерухомого водила.
– нерухоме (умовно зупинене), тобто передатне відношення визначене за умови нерухомого водила.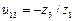 , маємо лише одне рівняння, а усі три кутові швидкості, що входять у формули, є невідомими.
, маємо лише одне рівняння, а усі три кутові швидкості, що входять у формули, є невідомими.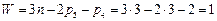 .
.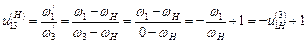 ,
,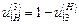 .
.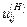 оберненого механізму вираховується від ведучого колеса до того колеса, яке у дійсному планетарному механізмі нерухоме.
оберненого механізму вираховується від ведучого колеса до того колеса, яке у дійсному планетарному механізмі нерухоме.