
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамічна модель машинного агрегату з одним ступенем вільностіСодержание книги
Поиск на нашем сайте Машинний агрегат – це, переважно, сукупність машини-двигуна, механізму передач та робочої машини. Це, як правило, багатоланкова система, навантажена багатьма силами та моментами, прикладеними до різних ланок. На рис. 3.1, як приклад, приведена силова установка, в якій ДВЗ приводить в рух через зубчасту передачу вал робочої машини – відцентрової помпи. До ланок машинного агрегату під час руху прикладені різні сили: рушійна сила FД, сила корисного опору – момент МРМ, сили тяжіння, в усіх кінематичних парах діють сили тертя. Характер дії цих сил різний: деякі залежать від положення чи швидкості ланок, інші постійні. При цьому кожна ланка має свою масу, момент інерції. Своїми діями прикладені сили надають механізму той чи інший закон руху. Визначення закону руху такої складної багатоланкової системи становить непросту задачу. У той же час для механізму, що має один ступінь вільності, задачу можна вважати розв’язаною, якщо буде відомий закон руху однієї ланки, яка таким чином буде початковою. Закон руху інших ланок і точок механізму після цього можна без значних зусиль визначити методами кінематичного аналізу. Викладене наводить на думку замінити весь складний багатоланковий механізм однією умовною рухомою ланкою. Виберемо за таку ланку 1 (рис. 5.1, а) та виділимо її разом зі стояком (рис. 5.1, б). До умовної ланки пред’явимо такі вимоги: нехай її момент інерції Ізв і момент сил Мзв, якими вона навантажена, будуть такими, що закон руху умовної ланки буде повністю співпадати з законом руху ланки 1 заданого механізму, тобто для будь-якого моменту часу буде справедливим рівняння
де Це означає, що умовна ланка зі стояком є своєрідною динамічною моделлю машинного агрегату. Таким чином, якщо визначити закон руху цієї простої моделі (рис. 5.1, б), то автоматично стане відомим дійсний закон руху початкової ланки заданого механізму. Зазначимо, якщо заданий механізм має кривошип, то його доцільно вибрати за рухому ланку динамічної моделі. Підсумуємо викладене. Побудова динамічної моделі машинного агрегату полягає в заміні заданого багатоланкового механізму, навантаженого довільною системою сил та моментів, простою динамічною моделлю (рис. 5.1, б) – однією умовною рухомою ланкою зі стояком. При цьому, всі сили і моменти, що прикладені до заданого механізму, замінені, як правило, одним зведеним моментом, що прикладений до умовної ланки. Отже, Мзв є еквівалентом до всього навантаження, прикладеного до машинного агрегату. Так само маси всіх ланок замінені моментом інерції умовної ланки - зведеним моментом інерції Ізв. Таким чином, побудова динамічної моделі полягає в зведенні сил – визначенні Мзв і в зведенні мас – визначенні Ізв. При цьому, щоб динамічна модель була адекватна заданому механізму, необхідно (слідує з рівняння Лагранжа ІІ роду, принципу можливих переміщень), щоб при зведенні сил була витримана умова рівності елементарних робіт всіх сил і моментів, прикладених до ланок реального механізму, і зведеної сили; при зведенні мас - умова рівності кінетичних енергій мас реального механізму і зведеного моменту інерції моделі.
Рис. 5.1
Наголосимо: побудова динамічної моделі дає змогу, розв’язуючи задачі динаміки, розглядати не весь складний машинний агрегат з багатьма ланками, що мають різні маси та на які діють різні сили, а одну умовну ланку з однією еквівалентною масою (чи моментом інерції) із прикладеною до неї, як правило, однією силою (чи моментом). Зазначимо, що в загальному випадку розрізняють дві динамічні моделі: з розподіленою масою (рис. 5.1, б), та із зосередженою масою (рис. 5.1, в). Остання застосовується, переважно, якщо в складі механізму немає жодної ланки, що здійснює обертальний рух. Зведення сил та мас
При дослідженні руху механізму зручно замінити усі сили та моменти, звівши їх до однієї ланки, еквівалентною з точки зору динаміки, силою чи моментом сил. При цьому необхідно, щоб елементарна робота на розглядуваному можливому переміщенні, або потужність, що розвивається замінюючою силою чи моментом, була рівна, відповідно, сумі елементарних робіт або потужностей, що розвивають усі сили та моменти, які прикладені до ланок механізму на цьому ж переміщенні. Сили чи моменти, що задовольняють цій умові, називають зведеними силами та моментами. Ланка, до якої зводяться сили та моменти (маси), називається ланкою зведення, а точка прикладання зведенної сили – точкою зведення. Зазвичай за ланку зведення приймають ту ланку, за узагальненою координатою якої проводяться дослідження механізму. Частіше це початкова ланка, головний вал робочої машини або вихідний вал машини-двигуна. Для визначення зведеної сили чи моменту може бути використана рівність
де Потужність
де Права частина рівності (1) в розгорнутому вигляді може бути представлена так
де З рівнянь (2) та (3) отримуємо
Існує таке визначення: зведеним моментом (силою) називають момент (силу), що умовно прикладений до ланки зведення, миттєва потужність якого дорівнює сумі миттєвих потужностей усіх сил і моментів, що діють на ланки механізму. Наголосимо, що при заданих силах Зазначимо, що деколи окремо зводять рушійні сили, сили опору, сили ваги і т.ін. Формули (4), (5) залишаються справедливими в усіх випадках, потрібно лише вказати, які сили зводяться. Зведення мас. Заміна мас рухомих ланок механізму зведеною масою, зосередженою в довільно вибраній точці ланки зведення, або зведеним моментом інерції виконується на основі еквівалентності миттєвих значень кінетичних енергій моделі Тмод та всього механізму Тмех Тмод = Тмех. Кінетична енергія плоского механізму для будь-якого його положення дорівнює сумі кінетичних енергій усіх його рухомих ланок Ті і в загальному випадку може бути представлена у вигляді Тмех = де Вирази кінетичної енергії Тмод для ланки зведення, або точки зведення: Тмод = Згідно з умовою динамічної еквівалентності механізму та моделі отримаємо
або
Зустрічаються такі визначення: - зведеним моментом інерції називається такий умовний момент інерції, кінетична енергія якого у кожному розглядуваному положенні механізму дорівнює сумі кінетичних енергій всіх його ланок; - зведена маса являє собою таку умовну масу, зосереджену в деякій точці зведення, кінетична енергія якої в кожному розглядуваному положенні механізму дорівнює сумі кінетичних енергій всіх його ланок. Зведені сила та маса, згідно з рівняннями (4)-(8), залежать від співвідношень, відповідно, швидкостей ланок механізму до швидкості ланки зведення та квадратів цих відношень. Ці співвідношення, в загальному випадку, залежать тільки від положення механізму, але вони будуть однаковими при будь-якому законі руху механізму. Отже, зведена сила і маса, як правило, є величинами змінними, періодичними функціями, які залежать від узагальненої координати механізму. З викладеного робимо висновок, що модель, якою замінюється механізм, є умовним тілом тому, що в загальному випадку її момент інерції (маса) є змінними, тоді як реальні фізичні тіла мають постійні моменти інерції (маси). Лише в окремих випадках, коли передатне відношення механізму є сталим (наприклад, зубчасті, фрикційні механізми, шарнірний паралелограм та інші), зведений момент інерції постійний. Таким чином, оскільки Рівняння руху механізму Для визначення законів руху початкових ланок за заданими силами використовуються рівняння, що називаються рівняннями руху механізму. Число цих рівнянь дорівнює числу ступенів рухомості механізму. Рівняння руху механізму можуть бути представлені в різних формах. Для механізмів з одним ступенем вільності одна з найпростіших форм рівнянь отримується на основі теореми про зміну кінетичної енергії: зміна кінетичної енергії механізму на деякому переміщенні дорівнює сумі робіт усіх сил, що діють на ланки механізму на цьому самому переміщенні. Цей закон подають у вигляді рівняння
де Т – кінетична енергія механізму в довільному положенні; Т 0 – кінетична енергія механізму в положенні, що приймається за початкове; Роботу здійснюють усі активні сили і моменти та сили тертя у всіх кінематичних парах механізму. Рівняння руху в енергетичній формі. Зведемо усі сили і моменти механізму з одним ступенем вільності до однієї ланки зведення, тобто замінимо розглядуваний механізм його динамічною моделлю. Оскільки все навантаження, прикладене до моделі, виражається зведеним моментом МЗВ, то права частина рівняння (9) дорівнює
а саме рівняння (9), враховуючи (6), можна записати у вигляді
Рівняння (11) називають рівнянням руху механізму в енергетичному вигляді, або – в формі рівняння кінетичної енергії. Загалом верхня межа Якщо все навантаження, що прикладене до механізму, залежить тільки від його положення (і не залежить від
При заданих функціях ІЗВ, МЗВ і відомій швидкості Якщо дослідження механізму починається з моменту пуску (тобто
Аналогічно (11) можна представити рівняння руху механізму, якщо всі сили і маси зводяться до вибраної точки зведення В
Рівняння руху в диференційній формі. Рівняння руху механізму в енергетичній формі (11) використовується, переважно, у випадках коли зведені силові фактори залежать від положень ланок. В інших випадках використовується диференційне рівняння руху механізму, яке можна отримати, продиференціювавши рівняння (11) по координаті
або, враховуючи, що в загальному випадку змінною величиною є не тільки
Рівняння (14) називається рівнянням руху в диференційній формі, оскільки шукана змінна величина – кутова швидкість У випадку, коли досліджуваний механізм має ІЗВ=const, то рівняння (14) спрощується і має вигляд
Для визначення кутового прискорення початкової ланки розв’яжемо рівняння (14) відносно
Похідна Режими руху
Дослідження динаміки машин полягає, в першу чергу, у визначенні та аналізі часткових розв’язків, наведених вище диференційних рівнянь руху, що відповідають характерним режимам роботи. Процес руху машини в загальному випадку складається з трьох режимів: розбігу, усталеного руху, вибігу. Це наочно показує діаграма залежності швидкості руху початкової ланки від часу (рис. 5.2). При усталеному русі швидкість головного вала змінюється періодично, інколи вона може бути постійною. Розбіг та вибіг – це перехідні режими, які характеризуються неперіодичними змінами швидкості вала машини (початкової ланки). З цих міркувань часто розрізняють два режими: усталений рух та перехідні процеси. Усталений рух. Під усталеним рухом будемо розуміти такий режим роботи, при якому вхідний параметр двигуна (параметри u, що керує процесом перетворення енергії) лишається постійним (u=uо=const), а кутова швидкість вихідного вала двигуна або лишається постійною, або коливається біля деякого середнього значення
Усталеним рухом машини називається рух, при якому її кінетична енергія є періодичною функцією часу. Проміжок часу (tц), протягом якого швидкість головного вала набуває свого початкового значення, пройшовши через
Рис. 5.2 Оскільки швидкості на початку та в кінці циклу усталеного руху рівні між собою (
Рівність (15) – основне енергетичне рівняння усталеного руху. При усталеному русі робота рушійних сил за один цикл дорівнює роботі сил опору (виробничого та шкідливого). У середині циклу ця рівність, як правило, не зберігається, а тому мають місце коливання швидкості початкових ланок. Якщо, Перехідні процеси. Розбіг - це режим руху, у процесі якого машина зі стану спокою приходить до усталеного руху. Рівняння руху набуває вигляду
Оскільки кінетична енергія завжди додатна, то для можливості пуску машини необхідно, щоб робота рушійних сил була більшою за роботу сил опору, Вибіг (зупинка) – це режим руху, в процесі якого машина переходить від усталеного руху до стану спокою. Переважно при вибігу двигун відключається або переводиться в генераторний режим, при якому вводиться додатковий гальмівний момент. Таким чином, у період розбігу кінетична енергія машини збільшується за рахунок надлишку роботи рушійних сил над роботою сил опору (Ар>Ао); під час усталеного руху кінетична енергія на початку та в кінці кожного циклу однакова (Ар=Ао); у період вибігу кінетична енергія повністю поглинається роботою сил опору. Перехідні процеси при зміні навантаження. Часто усталений рух чергується із розбігом (при підвищеннях швидкісного режиму) та гальмуваннями (при зменшенні швидкості). Так працює, наприклад, автомобільний двигун. Відмітимо, що багато механізмів не працюють у режимі усталеного руху.
|
||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.21 (0.007 с.) |

 ,
, - кутова швидкість кривошипу 1 заданого механізму,
- кутова швидкість кривошипу 1 заданого механізму,  - кутова швидкість умовної ланки (моделі).
- кутова швидкість умовної ланки (моделі).
 , (1)
, (1)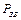 - потужність, що розвиває зведена сила чи зведений момент;
- потужність, що розвиває зведена сила чи зведений момент;  - сумарна потужність усіх сил та моментів, що підлягають зведенню.
- сумарна потужність усіх сил та моментів, що підлягають зведенню. , або
, або  , (2)
, (2) – зведений момент;
– зведений момент; 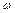 - кутова швидкість ланки зведення;
- кутова швидкість ланки зведення; 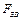 – величина зведеної до точки В сили;
– величина зведеної до точки В сили; 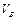 - швидкість точки зведення (рис. 5.1, в).
- швидкість точки зведення (рис. 5.1, в). , (3)
, (3)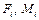 – сила і момент, які прикладені до і -ої ланки;
– сила і момент, які прикладені до і -ої ланки;  – швидкість точки прикладання сили
– швидкість точки прикладання сили  ;
;  – кут, утворений силою
– кут, утворений силою  – кутова швидкість і -ої ланки.
– кутова швидкість і -ої ланки. , (4)
, (4) . (5)
. (5) визначення зведеного моменту чи зведеної сили не являє значних труднощів і може бути легко проведене, наприклад, якщо для кожного досліджуваного положення механізму буде побудований план швидкостей.
визначення зведеного моменту чи зведеної сили не являє значних труднощів і може бути легко проведене, наприклад, якщо для кожного досліджуваного положення механізму буде побудований план швидкостей.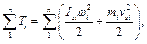
 – момент інерції і -ої ланки відносно осі, що проходить через центр мас
– момент інерції і -ої ланки відносно осі, що проходить через центр мас  перпендикулярно площині руху;
перпендикулярно площині руху; 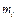 – маса і -ої ланки;
– маса і -ої ланки;  – швидкість центру мас і -ої ланки.
– швидкість центру мас і -ої ланки. , або Тмод =
, або Тмод =  . (6)
. (6) ,
,
 звідки
звідки (7)
(7) (8)
(8) не залежать від закону руху, зведення мас та сил можна виконувати і не знаючи законів руху механізму. Отже, розв’язуючи задачі динаміки, цілком можливо (і потрібно) спочатку побудувати динамічну модель механізму, виконавши зведення сил та мас, а потім вже знаходити закон її руху.
не залежать від закону руху, зведення мас та сил можна виконувати і не знаючи законів руху механізму. Отже, розв’язуючи задачі динаміки, цілком можливо (і потрібно) спочатку побудувати динамічну модель механізму, виконавши зведення сил та мас, а потім вже знаходити закон її руху. (9)
(9) – алгебраїчна сума робіт усіх сил і моментів, що прикладені до механізму на деякому переміщенні.
– алгебраїчна сума робіт усіх сил і моментів, що прикладені до механізму на деякому переміщенні. (10)
(10) . (11)
. (11) інтегрування в (11) вважається змінною.
інтегрування в (11) вважається змінною. . (12)
. (12) в початковий момент, рівняння (12) дозволяє визначити значення
в початковий момент, рівняння (12) дозволяє визначити значення  ), то (12) набуде вигляду
), то (12) набуде вигляду .
.
 . (13)
. (13)

 . (14)
. (14)

 .
. обчислюється чисельним диференціюванням з використанням ЕОМ, або графічним диференціюванням, якщо це не можливо зробити аналітично. У більшості випадків диференційне рівняння руху (14) може бути про інтегровано лише чисельними методами. Точний розв’язок рівняння можна одержати лише тоді, коли сили що діють на ланки механізму є функціями положень ланок
обчислюється чисельним диференціюванням з використанням ЕОМ, або графічним диференціюванням, якщо це не можливо зробити аналітично. У більшості випадків диференційне рівняння руху (14) може бути про інтегровано лише чисельними методами. Точний розв’язок рівняння можна одержати лише тоді, коли сили що діють на ланки механізму є функціями положень ланок , причому найбільші відхилення малі у порівнянні з цим середнім значенням. Іншими словами, в цьому випадку
, причому найбільші відхилення малі у порівнянні з цим середнім значенням. Іншими словами, в цьому випадку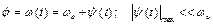 . (15)
. (15) та
та  , називають циклом усталеного руху.
, називають циклом усталеного руху.

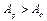 - рух механізму прискорений і навпаки.
- рух механізму прискорений і навпаки. .
.


