Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурні формули кінематичних ланцюгівСодержание книги
Поиск на нашем сайте
Існують загальні закономірності в будові (структурі) найрізноманітніших механізмів, які проявляються у взаємозв’язку числа ступенів вільності механізму з числом ланок та числом і видом його кінематичних пар. Ці закономірності відображають структурні формули механізмів. Просторові механізми. Нехай механізм складається з к ланок. Якби всі ланки були вільними тілами, загальна кількість їх ступенів вільності була б рівна Н = 6к. В механізмі ланки з’єднані за допомогою кінематичних пар. Кожна з пар накладає на ланку відповідну кількість в’язей. Так, кінематична пара V класу накладає п’ять в’язей (“відбере” п’ять ступенів вільності), IV – чотири в’язі, ІІІ – три в’язі і т.ін. Позначимо число кінематичних пар V класу, що входять до складу механізму, через р 5, IV класу - р4, ІІІ класу – p 3 і т. п. Тоді загальне число ступенів вільності всіх ланок, тобто число ступенів вільності, що їх має кінематичний ланцюг механізму, становитиме Н=6к-5р5-4р4-3р3-2р2-р1 Оскільки в механізмі одна із ланок вважається нерухомою, то загальне число ступенів вільності зменшиться на шість, W = Н-6. Позначимо число рухомих ланок механізму через n = к-1, тоді число ступенів вільності кінематичного ланцюга відносно нерухомої ланки W = 6n-5р5-4р4-3р3-2р2-р1. (1.1) Це формуладлявизначеннячисла ступенів вільності (рухомості) просторових кінематичних ланцюгів, механізмів – структурна формула кінематичного ланцюга загального виду. В літературі її називають ще формулою Сомова-Малишева. Ступінь вільності (рухомості) механізму W – це число ступенів вільності його рухомого кінематичного ланцюга відносно нерухомої ланки (стояка). Плоскі механізми. На рух кожної з ланок плоского механізму накладено три загальні обмеження. Якщо б усі рухомі ланки на площині були вільними тілами, то загальне число ступенів вільності ланок дорівнювало б (6 - 3)n = 3n. У плоских механізмах кінематичні пари можуть бути лише V класу, однорухомі - нижчі та IV класу, дворухомі - вищі; відповідно пари п’ятого класу будуть накладати – (5 - 3)р5 = 2р5 в’язей (три загальні в’язі вже накладено площиною); пари четвертого класу – (4 - 3)р4 = р4 в’язей. В плоскі механізми пари I, II, III класів входити не можуть, оскільки вони володіють просторовим характером можливих відносних рухів. Структурна формула для плоского кінематичного ланцюга буде: W=3n-2р5-р4. (1.2) Це структурна формула Чебишева для визначення числа ступенів вільності плоских кінематичних ланцюгів, механізмів. За формулами (1.1), (1.2) проводять структурний аналіз існуючих механізмів і синтез структурних схем нових механізмів. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття. Механізмом називається такий кінематичний ланцюг, у якому при заданому русі однієї чи декількох ланок відносно будь-якої з них всі інші ланки здійснюють однозначно визначені рухи. Як видно з визначення, у будь-якому механізмі є ланка (або декілька ланок), рух яких є заданим. Виникає запитання - скільки незалежних рухів можна задати даному механізму? Як було сказано, ступінь вільності механізму характеризує число ступенів вільності його кінематичного ланцюга відносно стояка. Отже, якщо механізм має один ступінь вільності, то одній з ланок механізму треба задати рух; при цьому всі інші ланки механізму отримують цілком визначені рухи, що є функціями заданого. Таким чином, для визначеності рухів усіх ланок механізму, який утворений кінематичним ланцюгом з одним ступенем вільності, необхідно і достатньо мати заданим закон руху однієї з ланок. Якщо механізм має два ступені вільності, то необхідно задати одній з ланок два незалежних рухи або двом ланкам по одному незалежному руху. Отже, ступінь вільності механізму вказує на число незалежних рухів, які треба задати в механізмі, щоб рух усіх інших ланок був цілком визначеним. Зазначимо, що при нульовому ступені вільності ні одна з ланок не може рухатися відносно нерухомої ланки і кінематичний ланцюг перетворюється у ферму. Кожна з незалежних між собою координат, що визначає положення всіх ланок механізму відносно стояка, називається узагальненою координатою механізму. За узагальнену координату приймається кут повороту або лінійне зміщення ланки. Ланка, якій приписується одна чи декілька узагальнених координат, називається початковою ланкою. Цей термін пов’язаний з тим, що знаходження положень усіх ланок механізму починають з побудови положень початкової ланки. Вибір початкової ланки визначається зручністю визначення положень ланок механізму та зручністю його аналізу. Початкові та вхідні ланки можуть як збігатися, так і не збігатися. Число узагальнених координат механізму також визначається ступенем вільності механізму. Кожний незалежний рух визначається заданням закону зміни однієї узагальненої координати (кутової або лінійної). Кривошипно-повзунний механізм (рис. 1.1) має ступінь вільності рівний одиниці, тобто W=1. Отже, для визначеності руху всіх ланок механізму треба задати йому один рух або треба мати заданою одну узагальнену координату. Нехай задано закон обертання ланки 1 у вигляді функції Ступінь вільності механізму визначає число вхідних (початкових) ланок, тобто кількість ланок, яким необхідно задати рух, щоб усі інші ланки рухались цілком визначено. Зазначимо, що, в основному, в конструкціях машин і приладів використовуються механізми з одним ступенем вільності. Значно рідше знаходять застосування механізми з двома та більше ступенями вільності. До таких конструкцій відносяться, наприклад, диференціали автомобілів, маніпулятори. Пасивні (зайві) умови зв’язку. Необхідно зазначити, що під час дослідження структури механізму можуть виявитися умови зв’язку та ступені вільності, що не впливають на характер руху механізму в цілому. Такі умови зв’язку називають пасивними, а ступені вільності – зайвими, оскільки їх можна вилучити без зміни загального характеру руху механізму. Розглянемо для прикладу важільний п’ятиланковий механізм подвійного паралелограма, що на практиці трапляється у вагових механізмах, швейних двоголчастих машинах, спарниках тепловозів та електровозів (рис. 1.8, а). При значних навантаженнях ланки можуть недопустимо деформуватися. Крім того, шарнірний паралелограм, переходячи через своє граничне положення, може перетворитися в антипаралелограм. Для позбавлення цих недоліків у конструкцію механізму вводять додатковий шатун EF. При цьому розміри ланок задовольняють умови АВ = СD, АD = ЕF = ВС, АЕ = ВЕ і DF = FС. З урахуванням другого шатуна ступінь рухомості механізму паралелограма W = 3n-2р5-р4 =3·4-2·6 = 0,
Рис. 1.8
тобто, згідно з розрахунком, такий кінематичний ланцюг не має рухомості, а є фермою. Насправді, як це підтверджує практика, у разі приведення в рух кривошипа АВ (чи іншої ланки) усі ланки даного кінематичного ланцюга мають цілком визначені рухи. Отже, це механізм, а кінематичні пари Е та F і зв’язки, накладені ними на ланки, не впливають на рух механізму в цілому. Додаткові в’язі, що не впливають на рух механізму в цілому та на закон руху веденої ланки, називають пасивними (зайвими). Пасивні в’язі дублюють інші в’язі, не зменшуючи рухомість механізму, а лише перетворюють його у статично невизначену систему. Виконуючи структурний, кінематичний аналіз, пасивні в’язі треба вилучати; умовно відокремимо шатун ЕF від механізму. Тоді ступінь вільності механізму буде таким, як і є насправді, рівним одиниці W=3 Зазначимо, що пасивні зв’язки існують при виконанні певних геометричних співвідношень у механізмі; введення додаткового шатуна ЕF лише за умови ЕF = АD не внесе нових зв’язків і число ступенів вільності залишиться рівним одиниці. Якщо ж точність виконання вказаних геометричних співвідношень виявиться недостатньою, наприклад, АЕ Отже, в загальне число накладених умов зв’язку може ввійти деяке число додаткових (пасивних) в’язей. Ступінь вільності просторового механізму з урахуванням пасивних зв’язків визначається за такою формулою Сомова-Малишева
де q – число пасивних (зайвих) в’язей. У загальному випадку розв’язати рівняння (1.3) з двома невідомими (W, q) є важкою задачею. Проте, коли ступінь вільності механізму знайдено з геометричних міркувань, то з (1.3) можна знайти число пасивних зв’язків. Для плоского механізму формула Чебишева з урахуванням пасивних зв’язків матиме вигляд Wп = 3n-2р5-р4+q індекс “п” звертає увагу на те, що йдеться про ідеально плоский механізм або, точніше, про його плоску схему. Реальні плоскі механізми, через неточності виготовлення, деякою мірою є просторовими. Механізми, які мають зайві зв’язки, є статично невизначеними; якщо q = 0 - механізм - статично визначена система. Якщо пасивних умов зв’язку немає, механізм складається без деформації ланок, останні ніби самовстановлюються; такі механізми називаються самоустановлюваним або раціональними. Якщо пасивні в’язі існують (q Але в цілому ряді випадків необхідно свідомо проектувати та виготовляти статично невизначені механізми із залишковими в’язями для забезпечення потрібної міцності та жорсткості системи, для кращого розподілу навантажень, особливо при передачі великих сил. Так, наприклад, для колінчатого вала чотирициліндрового двигуна (рис. 1.8, б), з погляду кінематики механізму з одним ступенем вільності, повністю достатньо однієї опори А з обертовою кінематичною парою V класу. Але, враховуючи велику довжину вала і значні зусилля, що навантажують колінчатий вал, вводять ще дві опори А/ і А//; інакше система буде нероботоздатною з причини недостатньої жорсткості та міцності. Для такої конструкції необхідно забезпечити високу точність виготовлення, особливо співвісність усіх трьох опор, інакше вал буде деформуватись, і в матеріалі вала та вальницях можуть з’явитися недопустимо великі напруги. Зазначимо, що розрізняють пасивні умови зв’язку в кінематичних ланцюгах механізму – зайві контурні зв’язки, та – в кінематичних парах – локальні зв’язки (відповідно перший та другий розглянуті приклади). Зайві ступені вільності. Розповсюдженим прикладом зайвих ступенів вільності є обертання роликів на їх осях. Як приклад розглянемо кулачковий механізм з роликовим штовхачем (рис. 1.6). Ступінь вільності кулачкового механізму за формулою Чебишева W=3n-2p5-p4=3·3-2·3-1=2. Виходячи з того, що W=2 можна зробити висновок, що у механізмі має бути дві вхідні ланки. Проте очевидно, що для визначеності руху штовхача достатньо задати лише один рух кулачку. Зайвий ступінь вільності створює ролик. Він може обертатися навколо своєї осі, не впливаючи на характер руху всього механізму. Кінематика механізму не зміниться, якщо ролик вивести, а профіль кулачка виконати за еквідістантою (штрихова лінія на рис. 1.6). Ролик являє собою конструктивний елемент, який зменшує сили тертя і спрацювання ланок. У подальшому при вивченні руху ланок механізмів, будемо припускати, що всі зайві умови зв’язку попередньо вилучені.
1.5. Структурна класифікація плоских механізмів.
У сучасному машинобудуванні особливо поширені плоскі механізми, ланки яких входять в кінематичні пари IV i V класів. Розглянемо принципи їх структурної класифікації. Структурна класифікація Ассура-Артоболевського є однією з найраціональніших класифікацій плоских механізмів. Перевагою цієї класифікації є те, що вона пов’язується з методами кінематичного та динамічного дослідження механізмів. Класифікація універсальна, охоплює усі існуючі і можливі нові механізми; визначає напрямки дослідження механізмів, вказує шляхи утворення нових механізмів. В основі її лежить основний принцип створення механізмів, сформульований в 1914 р. Л.В. Ассуром. Ним був запропонований метод створення механізмів шляхом послідовного нашарування кінематичних ланцюгів, що мають певні структурні властивості: будь-який механізм може бути створений шляхом послідовного приєднання до однієї (чи декількох) початкових ланок та стояка кінематичних ланцюгів з нульовим ступенем вільності. Такі кінематичні ланцюги з нульовим ступенем вільності називають структурними групами або г рупами Ассура, а початкову ланку та стояк - механізмом І класу. Таким чином, будь - який механізм можна отримати послідовним приєднанням до механізму І класу (одного чи декількох) груп Ассура. Структурною групою Ассура називається кінематичний ланцюг, приєднання якого до механізму не змінює ступеня вільності механізму. Існують інші визначення, наприклад: кінематичний ланцюг, число ступенів вільності якого відносно елементів його зовнішніх кінематичних пар дорівнює нулю, називають групою Ассура, якщо з нього не можна виділити простіші кінематичні ланцюги, що задовільняють цій умові. Отже, основною ознакою групи Ассура є рівність нулю її ступеня вільності, WГр = 0. Сукупність стояка та початкової ланки, що утворюють кінематичну пару V класу, умовно називають механізмом І класу (найпростішим, початковим механізмом); число механізмів І класу дорівнює числу ступенів вільності механізму. Отже, механізми І класу являють собою найпростіші дволанкові механізми, що складаються з рухомої ланки та стояка, що з’єднані між собою або однією обертовою, або - поступальною кінематичною парою V класу (рис. 1.9); ступінь вільності механізму І класу рівний одиниці. Механізми І класу, що мають обертову пару, досить поширені в техніці. Це механізми таких машин, як електродвигуни, генератори, турбіни, вентилятори, відцентрові помпи і т.ін.
Рис. 1.9 Усі складніші можуть бути отримані шляхом приєднання до механізмів І класу додаткових кінематичних ланцюгів - структурних груп Ассура. Очевидно, щоб створити новий механізм з одним ступенем вільності, W =1 (з іншими властивостями), до механізму І класу треба приєднати лише такі кінематичні ланцюги, які мають W=0, тобто групи Ассура. При розгляді питань класифікації механізмів зручно обмежитися розглядом механізмів, у яких всі вищі пари IV класу попередньо замінені відповідними кінематичними ланцюгами, що утворені лише кінематичними парами V класу, p4=0. Тоді, для структурних груп Ассура, справедлива рівність WГр=3n-2p5=0. (1.4) З (1.4) дістанемо співвідношення p5= Таблиця 1.1
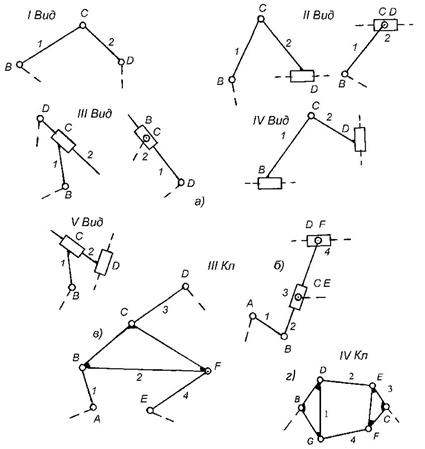
Зауважимо, що групи Ассура можуть мати лише парне число ланок, бути дво-, чотири-, шестиланковими і т.ін. Задаючись співвідношеннями ланок і кінематичних пар (табл. 1.1), можна дістати різні групи Ассура. Усі одержані таким чином групи Ассура поділено на класи: II, III, IV і т.д. У свою чергу, приєднуючи до механізму (чи механізмів) I класу групи Ассура різних класів, можна отримати найрізноманітніші механізми, відповідно механізми II, III, IV і т.д. класів. Відзначимо що поділ груп за класами зумовлено методами кінематичного і силового аналізів, що властиві групам кожного класу. Отже, найпростіша група Ассура складається з двох ланок і трьох кінематичних пар V класу - група Ассура ІІ класу ІІ порядку або двоповодкова група. Оскільки пари V класу в плоских механізмах можуть бути обертовими та поступальними, то залежно від співвідношення їх числа та розташування можливі 5 видів (модифікацій) такої групи. На рис. 1.10, а зображено групи Ассура ІІ класу ІІ порядку І, ІІ, ІІІ, IV, V видів; штриховими лінями показані ланки (поводки), до яких приєднуються дані структурні групи; це можуть бути рухома ланка або стояк механізму І класу, або ж ланки інших, вже приєднаних груп Ассура, при цьому не можна приєднувати структурну групу до однієї ланки. Зазначимо, що, приєднуючи до механізму І класу групу Ассура ІІ класу ІІ порядку І виду, дістанемо шарнірний чотириланковик, рис. 1.3, а; - ІІ виду – кривошипно-повзунний механізм, рис. 1.1; - ІІІ виду - кулісний механізм, рис. 1.3, в. Механізми, до складу яких входять групи Ассура не вище другого класу - це механізми ІІ класу. Наступна, більш складна група Ассура складається з чотирьох ланок і шести кінематичних пар - група ІІІ класу ІІІ порядку або триповодкова група. Характерною особливістю цієї групи є наявність ланки, що входить у три кінематичні пари й утворює жорсткий трикутник; таку ланку називають базисною. Найпростіша група ІІІ класу, з одними обертовими парами, зображена на рис. 1.10, в. В частинному випадку базисна ланка може бути прямолінійною, а деякі кінематичні пари - поступальними (рис. 1.10, б). Механізми, до складу яких входять групи Ассура не вище третього класу - механізми ІІІ класу. Другий можливий кінематичний ланцюг, що складається з чотирьох ланок і шести пар (рис. 1.10, г) – група ІV класу ІІ порядку. Особливістю цієї групи є наявність рухомого чотиристороннього замкненого контуру. Очевидно, можливо отримати різні модифікації цих груп, якщо обертові пари комбінувати з поступальними. Більш складні групи V і вищих класів використовуються обмежено і тут не розглядаються. Таким чином групи Ассура діляться на класи і порядки. Клас групи Ассура визначається найвищим класом контура, що входить до її складу (за І.І. Артоболевским, клас структурної групи Ассура визначається числом кінематичних пар, що утворюють найбільш складний замкнутий контур). Основою структурної групи є замкнутий контур. Клас контура визначається кількістю кінематичних пар, у які входять ланки, що його утворюють. Механізму І класу присвоюють І клас контура (контур виродився у точку; є лише одна кінематична пара); ланка з двома парами – ІІ клас (також частковий випадок замкнутого контура – контур виродився у пряму); жорстка ланка з трьома парами – ІІІ клас (рис. 1.11, в – трикутник); контур з чотирма парами – ІV клас і т.ін. Порядок групи Ассура визначається кількістю вільних (зовнішніх) елементів кінематичних пар (поводків), якими група Ассура приєднується до існуючого механізму. Вид групи Ассура для груп ІІІ та вищих класів не визначається.
Рис. 1.10
Клас механізму в цілому визначається найвищим класом групи, яка входить до його складу. Зазначимо що, визначаючи клас механізму, потрібно вказати, яка з ланок є початковою, оскільки залежно від її вибору може змінюватися клас механізму. Структурний аналіз механізму належить проводити шляхом розбивки його на структурні групи Ассура та механізми І класу у послідовності, зворотній до утворення механізму.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.014 с.) |


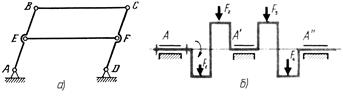
 =
= 
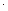 3-2
3-2 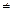 FD, то відстань ЕF вже не буде рівною AD і рух стане неможливим, тобто число ступенів вільності дійсно буде рівним нулю.
FD, то відстань ЕF вже не буде рівною AD і рух стане неможливим, тобто число ступенів вільності дійсно буде рівним нулю. 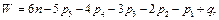 (1.3)
(1.3)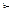 0), то механізми потребують підвищеної точності виготовлення. У разі недостатній точності у процесі складання ланки механізму деформуються, що викликає навантаження кінематичних пар і ланок значними додатковими силами; тертя в кінематичних парах може значно збільшитися. Тому з цього погляду пасивні в’язі в механізмах небажані.
0), то механізми потребують підвищеної точності виготовлення. У разі недостатній точності у процесі складання ланки механізму деформуються, що викликає навантаження кінематичних пар і ланок значними додатковими силами; тертя в кінематичних парах може значно збільшитися. Тому з цього погляду пасивні в’язі в механізмах небажані.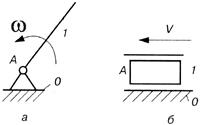
 n. Оскільки кількість кінематичних пар завжди ціле число, то кількість ланок в групі Ассура завжди парна; умові (1.4) відповідають лише такі співвідношення ланок і кінематичних пар, що входять у групу Ассура:
n. Оскільки кількість кінематичних пар завжди ціле число, то кількість ланок в групі Ассура завжди парна; умові (1.4) відповідають лише такі співвідношення ланок і кінематичних пар, що входять у групу Ассура: