
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення закону руху механізмуСодержание книги
Поиск на нашем сайте
Визначення закону руху механізму полягає у визначенні закону руху її початкової ланки. Початковою ланкою в більшості механізмів є кривошип. Для визначення закону руху початкової ланки механізму, яка визначає рух усіх інших ланок, використовуються рівняння руху (11) - (14). Розв’язуючи їх відносно швидкості руху початкової ланки, встановлюємо характер зміни її руху залежно від часу. Неусталений режим. Розглянемо один з найпростіших випадків: механізм навантажений силовими факторами, що є функціями лише переміщення своїх точок прикладання. Для визначення закону руху механізму при неусталеному режимі повинні бути відомі такі вихідні дані: кінематична схема механізму; маси, моменти інерції та положення центрів мас усіх рухомих ланок; механічні характеристики силових факторів; початкові умови руху. Останнє важливо для дослідження саме неусталеного режиму. Нехай зведений момент інерції розглядуваного механізму має змінну величину Для розв’язку даної задачі використовують рівняння руху механізму в енергетичному виді, яке розв’язується безпосередньо відносно шуканої величини
де Цю задачу зручно розв’язувати графічно. Для цього будують діаграми З рівняння (16), із урахуванням початкових умов, обчислюється для кожного положення механізму кутова швидкість Для визначення часу
звідки дістанемо
або
Якщо дослідження руху механізму ведеться з початку пуску, то
За формулами (17) та (18) можна визначити час руху механізму як функції кута повороту Кутове прискорення ланки зведення визначається графічним диференціюванням функції Визначення закону руху механізму, навантаженого силами, що залежать лише від швидкості. Нехай зведений момент інерції механізму є величина постійна. Типовими прикладами таких машинних агрегатів можуть бути турбо- і гідрогенератори, прокатні стани, відцентрові помпи, повітродувки та вентилятори з електроприводом. Як приклад розглянемо пуск відцентрової помпи, що приводиться в рух від двигуна постійного струму. Для розв’язування задачі скористаємось рівнянням руху в диференційній формі (14) для випадку
Рис. 5.3 Тоді рівняння руху можна записати у вигляді
Розв’язок цього рівняння, як відомо з курсу вищої математики, для випадку пуску помпи з нерухомого стану
За формулою (19) можна визначити закон зміни кутової швидкості ланки зведення під час розгону. Очевидно, що з часом швидкість За формулою (19) також можна визначити ту величину Зазначимо, що в багатьох випадках лінійна апроксимація залежності
де
Рис. 5.4
Момент сил опору обертанню, що діє на ротор є пропорційним квадрату кутової швидкості. У цьому випадку рівняння руху вигляду Визначення закону руху механізму, навантаженого силами, що залежать як від положення, так і швидкості, у випадку чисельного розв’язування задачі на ЕОМ виконуються аналогічно. Розв’язок таких задач аналітичними методами наведено у повному курсі ТММ.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 . Потрібно визначити залежність швидкості початкової ланки від її кута повороту, тобто
. Потрібно визначити залежність швидкості початкової ланки від її кута повороту, тобто  . Така задача є досить розповсюдженою (механізми дизель-компресорів, бурових верстатів і підіймальних кранів з приводом від ДВЗ, різних пристроїв з пневмоприводом і т. ін.).
. Така задача є досить розповсюдженою (механізми дизель-компресорів, бурових верстатів і підіймальних кранів з приводом від ДВЗ, різних пристроїв з пневмоприводом і т. ін.).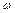
 , (16)
, (16) визначається з (10).
визначається з (10). (див.п. 5.7).
(див.п. 5.7). руху механізму можна скористатися умовою
руху механізму можна скористатися умовою ,
, ,
, . (17)
. (17) і (17) набуває вигляду
і (17) набуває вигляду . (18)
. (18) початкової ланки. Інтеграл у правій частині (17), (18) може бути визначений графічно, якщо побудувати графік
початкової ланки. Інтеграл у правій частині (17), (18) може бути визначений графічно, якщо побудувати графік  за відомою функцією
за відомою функцією 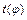 , якщо виключити з них кут
, якщо виключити з них кут  - залежність кутової швидкості
- залежність кутової швидкості  Механічні характеристики двигуна та робочої машини наведені відповідно на рис. 3.1, а та рис. 3.2, б. Звернемо увагу на те, що залежності близькі до лінійних. Зведемо до однієї ланки, наприклад, валу двигуна, усі маси та обидва моменти, тобто обчислимо
Механічні характеристики двигуна та робочої машини наведені відповідно на рис. 3.1, а та рис. 3.2, б. Звернемо увагу на те, що залежності близькі до лінійних. Зведемо до однієї ланки, наприклад, валу двигуна, усі маси та обидва моменти, тобто обчислимо  та
та  (рис. 5.3). Графік
(рис. 5.3). Графік  можна апроксимувати рівнянням прямої
можна апроксимувати рівнянням прямої  , де а та b – сталі коефіцієнти, які не складно визначити за відомими механічними характеристиками.
, де а та b – сталі коефіцієнти, які не складно визначити за відомими механічними характеристиками.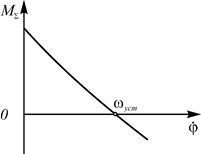
 .
. матиме вигляд
матиме вигляд (19)
(19) наближається до усталеного значення
наближається до усталеного значення 
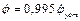 . Так з (14) маємо
. Так з (14) маємо 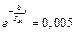 , або
, або  , звідки
, звідки  .
.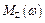 неможлива, як, наприклад, у випадку розгону помпи від асинхронного двигуна з короткозамкненим ротором механічна характеристика якого зображена на рис. 3.2, а. Розглянемо дану задачу. Обмежимось лінійною моделлю статичної характеристики електродвигуна (рис. 5.4). Нестійку ділянку
неможлива, як, наприклад, у випадку розгону помпи від асинхронного двигуна з короткозамкненим ротором механічна характеристика якого зображена на рис. 3.2, а. Розглянемо дану задачу. Обмежимось лінійною моделлю статичної характеристики електродвигуна (рис. 5.4). Нестійку ділянку  характеристики показано в цій моделі у вигляді відрізка прямої, яка проходить через точки
характеристики показано в цій моделі у вигляді відрізка прямої, яка проходить через точки  та
та  , стійку ділянку
, стійку ділянку  – у вигляді прямої, що проходить через точки
– у вигляді прямої, що проходить через точки  та
та  . Отже, обертальний момент на валу електродвигуна може бути обчислений таким чином
. Отже, обертальний момент на валу електродвигуна може бути обчислений таким чином
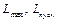 – максимальний (критичний) та пусковий моменти двигуна;
– максимальний (критичний) та пусковий моменти двигуна;  – критична та синхронна частоти обертання двигуна.
– критична та синхронна частоти обертання двигуна.
 можна розв’язати шляхом чисельного інтегрування на ЕОМ. На рис. 5.5 наведено результати розв’язування рівняня руху за допомогою пакета Maple – часові залежності: кутової швидкості ланки зведення (рис. 5.5, а); обертального моменту двигуна та моменту сил опору обертанню (рис. 5.5, б). З графіків випливає очевидний результат: чим більший момент інерції
можна розв’язати шляхом чисельного інтегрування на ЕОМ. На рис. 5.5 наведено результати розв’язування рівняня руху за допомогою пакета Maple – часові залежності: кутової швидкості ланки зведення (рис. 5.5, а); обертального моменту двигуна та моменту сил опору обертанню (рис. 5.5, б). З графіків випливає очевидний результат: чим більший момент інерції  , опір обертанню, менша потужність двигуна, тим триваліший час розгону; величина
, опір обертанню, менша потужність двигуна, тим триваліший час розгону; величина 


